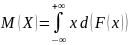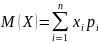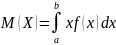- •Основные понятия теории вероятностей. События
- •Классификация событий.
- •Операции над событиями.
- •Классическое определение вероятности случайного события
- •Статистическое определение вероятности
- •Геометрическая вероятность
- •Аксиомы теории вероятностей.
- •Зависимые и независимые случайные события. Основные формулы сложения и умножения вероятностей
- •Теоремы сложения вероятностей
- •Зависимые и независимые события. Условная вероятность.
- •Формулы умножения вероятностей
- •Формула полной вероятности
- •Одномерные случайные величины
- •Понятие случайной величины
- •Законы распределения случайной величины
- •Функция распределения вероятностей и ее свойства
- •Плотность распределения вероятности и ее свойства
- •Числовые характеристики случайных величин
- •Свойства математического ожидания
- •Свойства дисперсии случайных величин
- •Числовые характеристики среднего арифметического n независимых случайных величин
- •Надёжность: основные понятия и определения
- •Основные понятия
- •Показатели надёжности
- •Показатели надежности – количественные и комплексные.
- •Основные показатели безотказности объектов Вероятность безотказной работы
- •Средняя наработка до отказа
- •Интенсивность отказов
- •Средняя наработка на отказ
- •Параметр потока отказов
- •Основные показатели долговечности Средний срок службы (математическое ожидание срока службы)
- •Средний ресурс (математическое ожидание ресурса)
- •Основные показатели ремонтопригодности
- •Среднее время восстановления
- •Интенсивность восстановления
- •Комплексные показатели надежности Коэффициент готовности
- •Коэффициент оперативной готовности
- •Коэффициент технического использования
- •Основные математические модели, наиболее часто используемые в расчётах надёжности. Распределение Вейбулла
- •Экспоненциальное распределение
- •Распределение Рэлея
- •Нормальное распределение (распределение Гаусса)
- •Примеры использования законов распределения в расчетах надежности
- •Определение показателей надежности при экспоненциальном законе распределения
- •Определение показателей надежности при распределении Рэлея
- •Определение показателей схемы при распределении Гаусса
- •Определение показателей надежности неремонтируемого объекта по опытным данным
- •Надёжность невосстанавливаемой системы при основном соединении элементов Определение вероятности безотказной работы и средней наработки до отказа
- •Пример расчета надежности системы, собранной по основной схеме
- •Порядок решения задач надёжности. Исходные положения
- •Методы расчета надежности
- •Надёжность невосстанавливаемых резервированных систем
- •Общее резервирование с постоянно включенным резервом и с целой кратностью
- •Надежность системы с нагруженным дублированием
- •Общее резервирование замещением
- •Надежность системы при раздельном резервировании и с целой кратностью по всем элементам
- •Смешанное резервирование неремонтируемых систем
- •Надёжность восстанавливаемых систем
- •Надежность восстанавливаемой одноэлементной системы
- •Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами
- •Надежность восстанавливаемой дублированной системы
- •Надежность восстанавливаемой системы при различных способах резервирования элементов
Плотность распределения вероятности и ее свойства
Функция распределения непрерывной случайной величины является ее вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения случайной величины в небольшой окрестности той или другой точки числовой оси. Более наглядное представление о характере распределения непрерывной случайной величины дает функция, которая называется плотностью распределения вероятности, или дифференциальной функцией распределения случайной величины.
Плотность
распределения
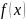 равна производной от функции распределения
,
т. е.
равна производной от функции распределения
,
т. е.
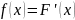
Смысл плотности распределения состоит в том, что она указывает на то, как часто случайная величина появляется в некоторой окрестности точки при повторении опытов. Кривая, изображающая плотность распределения случайной величины, называется кривой распределения.
Рассмотрим свойства плотности распределения.
Свойство 1. Плотность распределения неотрицательна, т. е.
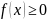
Свойство
2.
Функция распределения случайной величины
равна интегралу от плотности в интервале
от
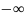 до
,
т. е.
до
,
т. е.
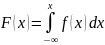
Свойство
3.
Вероятность попадания непрерывной
случайной величины
на участок
 равна интегралу от плотности распределения,
взятому по этому участку, т. е.
равна интегралу от плотности распределения,
взятому по этому участку, т. е.
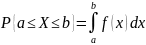
Свойство 4. Интеграл в бесконечных пределах от плотности распределения равен единице:
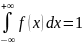
Пример 2. Случайная величина подчинена закону распределения с плотностью

Определить
коэффициент а; построить график плотности
распределения; найти вероятность
попадания случайной величины на участок
от 0 до
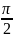 .
Определить функцию распределения и
построить ее график.
.
Определить функцию распределения и
построить ее график.
Решение. Площадь, ограниченная кривой распределения, численно равна
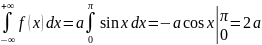
Учитывая
свойство 4 плотности распределения,
находим
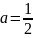 .
Следовательно, плотность распределения
можно выразить так:
.
Следовательно, плотность распределения
можно выразить так:
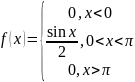
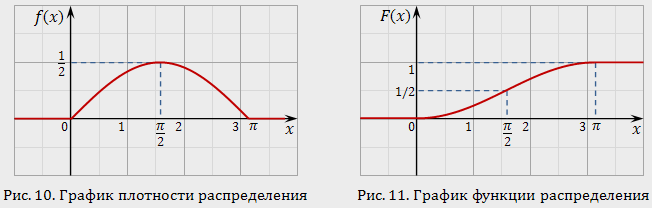
График плотности распределения на рис. 10. По свойству 3, имеем
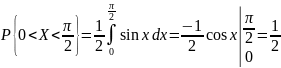
Для определения функции распределения воспользуемся свойством 2:
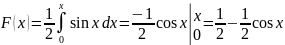
Таким образом, имеем
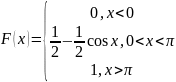
График функции распределения изображен на рис. 11
Числовые характеристики случайных величин
Закон распределения полностью характеризует случайную величину с вероятностной точки зрения. Но при решении ряда практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее пользоваться некоторыми количественными показателями. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются математическое ожидание и дисперсия.
Математическое
ожидание иногда называют средним
значением случайной величины. Рассмотрим
дискретную случайную величину
,
принимающую значения
с вероятностями соответственно
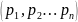 .
Определим среднюю арифметическую
значений случайной величины, взвешенных
по вероятностям их появлений. Таким
образом, вычислим среднее значение
случайной величины, или ее математическое
ожидание
.
Определим среднюю арифметическую
значений случайной величины, взвешенных
по вероятностям их появлений. Таким
образом, вычислим среднее значение
случайной величины, или ее математическое
ожидание
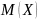 :
:
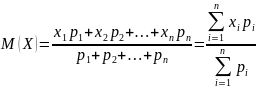
Учитывая,
что
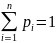 получаем
получаем
|
(4.1) |
Итак, математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие вероятности.
Для непрерывной случайной величины математическое ожидание
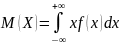
Математическое
ожидание непрерывной случайной величины
,
возможные значения которой принадлежат
отрезку
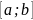 ,
,
|
(4.2) |
Используя функцию распределения вероятностей , математическое ожидание случайной величины можно выразить так: