
- •Основные понятия теории вероятностей. События
- •Классификация событий.
- •Операции над событиями.
- •Классическое определение вероятности случайного события
- •Статистическое определение вероятности
- •Геометрическая вероятность
- •Аксиомы теории вероятностей.
- •Зависимые и независимые случайные события. Основные формулы сложения и умножения вероятностей
- •Теоремы сложения вероятностей
- •Зависимые и независимые события. Условная вероятность.
- •Формулы умножения вероятностей
- •Формула полной вероятности
- •Одномерные случайные величины
- •Понятие случайной величины
- •Законы распределения случайной величины
- •Функция распределения вероятностей и ее свойства
- •Плотность распределения вероятности и ее свойства
- •Числовые характеристики случайных величин
- •Свойства математического ожидания
- •Свойства дисперсии случайных величин
- •Числовые характеристики среднего арифметического n независимых случайных величин
- •Надёжность: основные понятия и определения
- •Основные понятия
- •Показатели надёжности
- •Показатели надежности – количественные и комплексные.
- •Основные показатели безотказности объектов Вероятность безотказной работы
- •Средняя наработка до отказа
- •Интенсивность отказов
- •Средняя наработка на отказ
- •Параметр потока отказов
- •Основные показатели долговечности Средний срок службы (математическое ожидание срока службы)
- •Средний ресурс (математическое ожидание ресурса)
- •Основные показатели ремонтопригодности
- •Среднее время восстановления
- •Интенсивность восстановления
- •Комплексные показатели надежности Коэффициент готовности
- •Коэффициент оперативной готовности
- •Коэффициент технического использования
- •Основные математические модели, наиболее часто используемые в расчётах надёжности. Распределение Вейбулла
- •Экспоненциальное распределение
- •Распределение Рэлея
- •Нормальное распределение (распределение Гаусса)
- •Примеры использования законов распределения в расчетах надежности
- •Определение показателей надежности при экспоненциальном законе распределения
- •Определение показателей надежности при распределении Рэлея
- •Определение показателей схемы при распределении Гаусса
- •Определение показателей надежности неремонтируемого объекта по опытным данным
- •Надёжность невосстанавливаемой системы при основном соединении элементов Определение вероятности безотказной работы и средней наработки до отказа
- •Пример расчета надежности системы, собранной по основной схеме
- •Порядок решения задач надёжности. Исходные положения
- •Методы расчета надежности
- •Надёжность невосстанавливаемых резервированных систем
- •Общее резервирование с постоянно включенным резервом и с целой кратностью
- •Надежность системы с нагруженным дублированием
- •Общее резервирование замещением
- •Надежность системы при раздельном резервировании и с целой кратностью по всем элементам
- •Смешанное резервирование неремонтируемых систем
- •Надёжность восстанавливаемых систем
- •Надежность восстанавливаемой одноэлементной системы
- •Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами
- •Надежность восстанавливаемой дублированной системы
- •Надежность восстанавливаемой системы при различных способах резервирования элементов
Зависимые и независимые события. Условная вероятность.
Различают события зависимые и независимые. Два события называются независимыми, если появление одного из них не изменяет вероятность появления другого. Например, если работают два прибора, по условиям производства не связанные между собой, то поломки этих двух приборов являются независимыми событиями.
Пример 4. Монета брошена два раза. Вероятность появления "орла" в первом испытании (событие ) не зависит от появления или не появления "орла" во втором испытании (событие ). В свою очередь, вероятность появления "орла" во втором испытании не зависит от результата первого испытания. Таким образом, события и независимые.
Несколько событий называются независимыми в совокупности, если любое из них не зависит от любого другого события и от любой комбинации остальных.
События
называются зависимыми,
если одно из них влияет на вероятность
появления другого. Например, два прибора
связаны между собой единым технологическим
циклом. Тогда вероятность выхода из
строя одного из них зависит от того, в
каком состоянии находится другой.
Вероятность одного события
,
вычисленная в предположении осуществления
другого события
,
называется условной
вероятностью
события
и обозначается
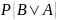 .
.
Условие
независимости события
от события
записывают в виде
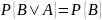 ,
а условие его зависимости — в виде
,
а условие его зависимости — в виде
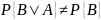 .
Рассмотрим пример вычисления условной
вероятности события.
.
Рассмотрим пример вычисления условной
вероятности события.
Пример 4. В ящике находятся 5 напильников: два изношенных и три новых. Производится два последовательных извлечения напильников. Определить условную вероятность появления изношенного напильника при втором извлечении при условии, что извлеченный в первый раз напильник в ящик не возвращается.
Решение.
Обозначим
извлечение изношенного напильника в
первом случае, а
– извлечение нового. Тогда
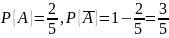 . Поскольку извлеченный напильник в
ящик не возвращается, то изменяется
соотношение между количествами изношенных
и новых резцов. Следовательно, вероятность
извлечения изношенного напильника во
втором случае зависит от того, какое
событие осуществилось перед этим.
. Поскольку извлеченный напильник в
ящик не возвращается, то изменяется
соотношение между количествами изношенных
и новых резцов. Следовательно, вероятность
извлечения изношенного напильника во
втором случае зависит от того, какое
событие осуществилось перед этим.
Обозначим событие, означающее извлечение изношенного резца во втором случае. Вероятность этого события будет такая:
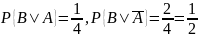
Следовательно, вероятность события зависит от того, произошло или нет событие .
Формулы умножения вероятностей
Пусть события и независимые, причем вероятности этих событий известны. Найдем вероятность совмещения событий и .
Теорема 2.3. Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
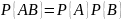
Следствие 2.1. Вероятность совместного появления нескольких событий, независимых в совокупности, равна произведению вероятностей этих событий:
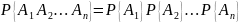
Пример 5. Система состоит из трёх последовательно соединённых приборов. Вероятность того, что первый прибор проработает без поломок 1 год равна 0.6, вероятность того, что без поломок проработает второй прибор равна 0.8, а вероятность того, что без поломок проработает третий прибор равна 0.9. Определить, какова вероятность того, что вся система проработает без поломок в течение года.
Решение. Поскольку поломки всех трёх приборов – события независимые, то для вычисления вероятности безотказной работы для всей системы воспользуемся формулой умножения вероятностей.
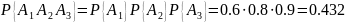
Теорема 2.4. Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
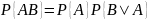
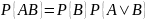
Следствие 2.2. Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились.
Пример
6.
В урне находятся 5 белых шаров, 4 черных
и 3 синих. Каждое испытание состоит в
том, что наудачу извлекают один шар, не
возвращая его в урну. Найти вероятность
того, что при первом испытании появится
белый шар (событие
),
при втором — черный (событие
)
и при третьем — синий (событие
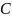 ).
).
Решение.
Вероятность появления белого шара при
первом испытании
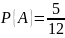 .
Вероятность появления черного шара при
втором испытании, вычисленная в
предположении, что при первом испытании
появился белый шар, т. е. условная
вероятность
.
Вероятность появления черного шара при
втором испытании, вычисленная в
предположении, что при первом испытании
появился белый шар, т. е. условная
вероятность
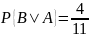 .
Вероятность появления синего шара при
третьем испытании, вычисленная в
предположении, что при первом испытании
появился белый шар, а при втором —
черный,
.
Вероятность появления синего шара при
третьем испытании, вычисленная в
предположении, что при первом испытании
появился белый шар, а при втором —
черный,
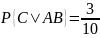 .
Искомая вероятность
.
Искомая вероятность
 .
.
