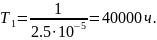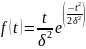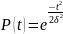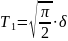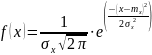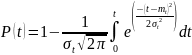- •Основные понятия теории вероятностей. События
- •Классификация событий.
- •Операции над событиями.
- •Классическое определение вероятности случайного события
- •Статистическое определение вероятности
- •Геометрическая вероятность
- •Аксиомы теории вероятностей.
- •Зависимые и независимые случайные события. Основные формулы сложения и умножения вероятностей
- •Теоремы сложения вероятностей
- •Зависимые и независимые события. Условная вероятность.
- •Формулы умножения вероятностей
- •Формула полной вероятности
- •Одномерные случайные величины
- •Понятие случайной величины
- •Законы распределения случайной величины
- •Функция распределения вероятностей и ее свойства
- •Плотность распределения вероятности и ее свойства
- •Числовые характеристики случайных величин
- •Свойства математического ожидания
- •Свойства дисперсии случайных величин
- •Числовые характеристики среднего арифметического n независимых случайных величин
- •Надёжность: основные понятия и определения
- •Основные понятия
- •Показатели надёжности
- •Показатели надежности – количественные и комплексные.
- •Основные показатели безотказности объектов Вероятность безотказной работы
- •Средняя наработка до отказа
- •Интенсивность отказов
- •Средняя наработка на отказ
- •Параметр потока отказов
- •Основные показатели долговечности Средний срок службы (математическое ожидание срока службы)
- •Средний ресурс (математическое ожидание ресурса)
- •Основные показатели ремонтопригодности
- •Среднее время восстановления
- •Интенсивность восстановления
- •Комплексные показатели надежности Коэффициент готовности
- •Коэффициент оперативной готовности
- •Коэффициент технического использования
- •Основные математические модели, наиболее часто используемые в расчётах надёжности. Распределение Вейбулла
- •Экспоненциальное распределение
- •Распределение Рэлея
- •Нормальное распределение (распределение Гаусса)
- •Примеры использования законов распределения в расчетах надежности
- •Определение показателей надежности при экспоненциальном законе распределения
- •Определение показателей надежности при распределении Рэлея
- •Определение показателей схемы при распределении Гаусса
- •Определение показателей надежности неремонтируемого объекта по опытным данным
- •Надёжность невосстанавливаемой системы при основном соединении элементов Определение вероятности безотказной работы и средней наработки до отказа
- •Пример расчета надежности системы, собранной по основной схеме
- •Порядок решения задач надёжности. Исходные положения
- •Методы расчета надежности
- •Надёжность невосстанавливаемых резервированных систем
- •Общее резервирование с постоянно включенным резервом и с целой кратностью
- •Надежность системы с нагруженным дублированием
- •Общее резервирование замещением
- •Надежность системы при раздельном резервировании и с целой кратностью по всем элементам
- •Смешанное резервирование неремонтируемых систем
- •Надёжность восстанавливаемых систем
- •Надежность восстанавливаемой одноэлементной системы
- •Надежность нерезервированной системы с последовательно включенными восстанавливаемыми элементами
- •Надежность восстанавливаемой дублированной системы
- •Надежность восстанавливаемой системы при различных способах резервирования элементов
Распределение Рэлея
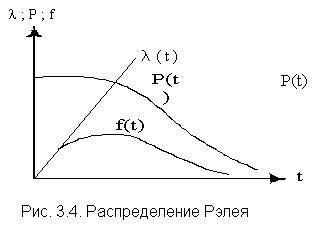
Плотность вероятности в законе Рэлея (см. рис. 3.4) имеет следующий вид
|
(3.11) |
где
– параметр распределения Рэлея (равен
моде этого распределения). Его не нужно
путать со среднеквадратическим
отклонением, равным
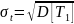
Интенсивность отказов равна:
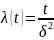
Характерным признаком распределения Рэлея является прямая линия графика , начинающаяся с начала координат.
Вычислим вероятность безотказной работы объекта в этом случае:
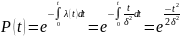
|
(3.12) |
Средняя наработка до отказа
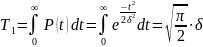
|
(3.13) |
Нормальное распределение (распределение Гаусса)
Нормальный закон распределения характеризуется плотностью вероятности вида
|
(3.14) |
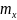 – математическое
ожидание случайной величины
.
– математическое
ожидание случайной величины
.
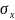 -
среднеквадратическое отклонение
случайной величины
.
-
среднеквадратическое отклонение
случайной величины
.
При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать и .
Вероятность безотказной работы определяется по формуле
|
(3.15) |
Интенсивность
отказов можно вычислить по формуле
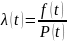
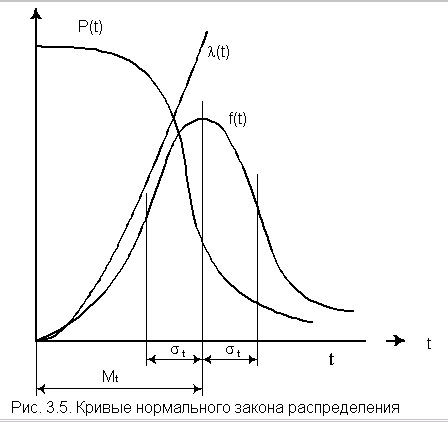
На
рис. 3.5 изображены кривые
,
и
для случая
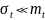 ,
характерного для элементов, используемых
в системах автоматического управления.
,
характерного для элементов, используемых
в системах автоматического управления.
В
данном пособии показаны только наиболее
распространенные законы распределения
случайной величины. Известен целый ряд
законов, так же используемых в расчетах
надежности: гамма-распределение, 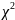 -распределение,
распределение Максвелла, Эрланга и др.
-распределение,
распределение Максвелла, Эрланга и др.
Следует отметить, что если неравенство не соблюдается, то следует использовать усеченное нормальное распределение.
Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом.
В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. При различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений.
Примеры использования законов распределения в расчетах надежности
Определим показатели надежности для наиболее часто используемых законов распределения времени возникновения отказов.
Определение показателей надежности при экспоненциальном законе распределения
Пример.
Пусть объект имеет экспоненциальное
распределение времени возникновения
отказов с интенсивностью отказов
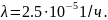 Требуется вычислить основные показатели
надежности невосстанавливаемого объекта
за
Требуется вычислить основные показатели
надежности невосстанавливаемого объекта
за
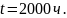 и вероятность безотазной работы на
интервале от
и вероятность безотазной работы на
интервале от
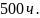 до
до
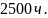
Решение.
Вероятность безотказной работы за время
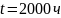 равна:
равна:
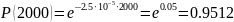
Вероятность отказа за равна
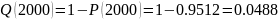
Используя выражение (2.5), вероятность безотказной работы в интервале времени от
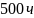 до
до
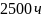 при условии, что объект проработал
безотказно
равна:
при условии, что объект проработал
безотказно
равна:
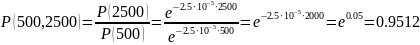
Средняя наработка до отказа