5.4. Перевірка адекватності динамічної моделі ор
Мірою
точності апроксимації можна вважати
максимальне значення різниці ординат
або
ж максимальну абсолютну похибку
,
де
- теоретична та експериментальна криві
розгону, яка не повинна перевищувати
заданого значення точності регулювання.
Точність апроксимації вважається задовільною, якщо зведена похибка δ = Δ×100% не перевищує 3%.
del =2.1989
Оскільки
зведена похибка
то ця функція передачі задовольняє
вимоги до точності апроксимації системи.
Отже, функція передачі об’єкту каналом переміщення РО на трубопроводі пари–температури в реакторі буде мати вигляд:
5.5. Розрахунок оптимальних настроювальних параметрів автоматичного під-регулятора
Функція передачі ПІД-регулятора має вигляд:
В
загальному випадку границя заданого
запасу стійкості є деякою поверхнею в
тривимірному просторі параметрів
настроювання
.
Якщо один з параметрів зафіксувати, то
розрахунок зводиться до визначення
двох інших параметрів настроювання.
Так, якщо задатись часом диференціювання
,
то значення двох інших параметрів
настроювання ПІД-регулятора
розраховують
за формулами:
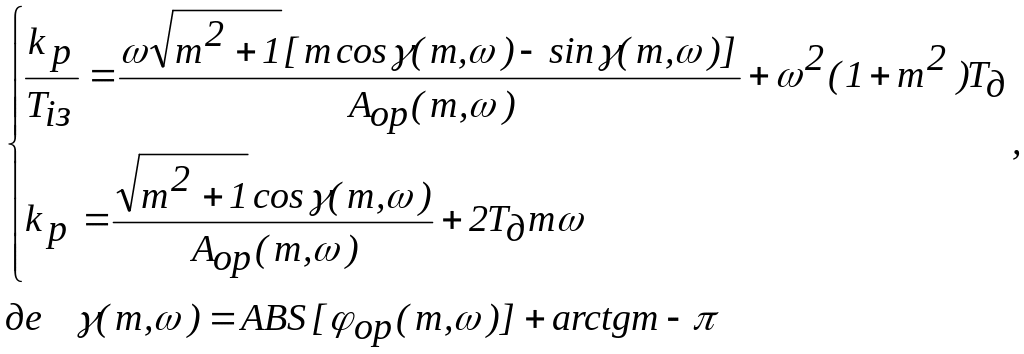
Для
заданих значень
в площині параметрів
будується границя області запасу
стійкості, з якої визначають оптимальні
значення параметрів настроювання
.
Розраховані оптимальні значення
параметрів настроювання ПІД-регулятора
повинні задовольняти умову:
.
Якщо остання умова не виконується, то необхідно зменшити час диференціювання і повторити розрахунок.
За розширеними частотними характеристиками знаходимо частоти w* і w**, які відповідають параметрам настроювання І- та П-регуляторів відповідно.
Програма в середовищі Matlab для знаходження значень ω* та ω**
%знаходження w* та w**
clear,clc;
T1=31.13; T2=31.13; T3=70.70; tay=6.47; m=0.32; k=0.92; Td=75;
w=[0:0.001:0.1];
p=-m*w+i*w;
Wor=k./(T1.*p+1).*(T2.*p+1).*(T3.*p+1).*exp(-tay.*p);
fi=phase(Wor);
l1=-pi/2+atan(m);
l2=-pi;
plot(w,fi,'k',[0 0.1],[-pi/2+atan(m) -pi/2+atan(m)],'k',[0 0.1],[-pi -pi],'k'); grid;
xlabel('w, rad/sec'); ylabel('y, rad');
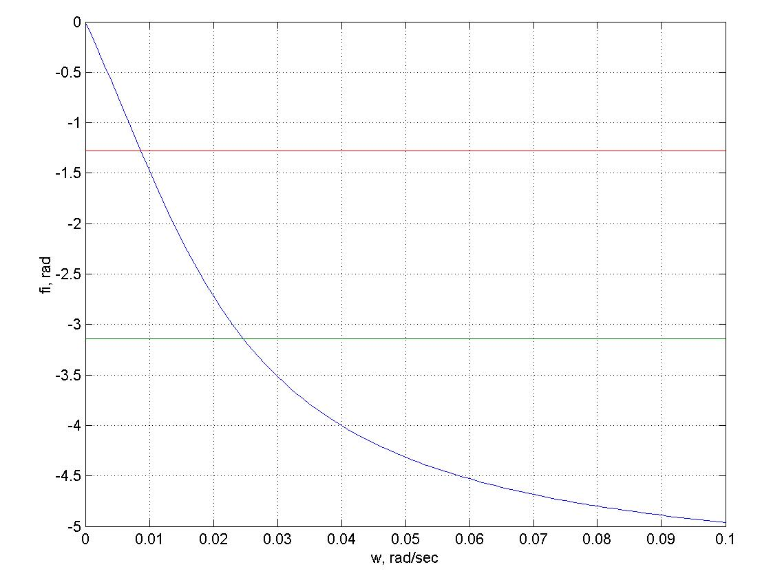
Рис.15 Pозширена фазо-частотна характеристики ОР
W* = 0.0085 рад/с
W** = 0.0255 рад/с
Для
заданого m в площині параметрів
,
,
будуємо границю області запасу стійкості,
з якої визначаємо оптимальні значення
параметрів настроювання (
)опт,
(
)опт,
=45с,
отримані при другій мінімальній
інтегральній оцінці.
% 2-ga integralna ocinka
clear,clc;
T1=31.13; T2=31.13; T3=70.70; tay=6.47; m=0.32; k=0.92; Td=45;
w=[0.014:0.0001:0.03];
p=-m.*w+i.*w;
Wop=k./((T1.*p+1).*(T2.*p+1).*(T3.*p+1)).*exp(-tay.*p);
Aop=abs(Wop);
fi=phase(Wop);
hama=abs(fi)+atan(m)-pi;
kp_Tiz=w*sqrt(m^2+1).*(m*cos(hama)-sin(hama))./Aop+w.^2*(m^2+1)*Td;
kp=sqrt(m^2+1).*cos(hama)./Aop+2*Td*m*w;
for i=1:length(w)
t=[0:600];
[num,den]=pade(tay,10);
Wop0=tf(num,den);
Wop1=tf(k,[T1 1]);
Wop2=tf(1,[T2 1]);
Wop3=tf(1,[T3 1]);
Wop=Wop1*Wop2*Wop3*Wop0;
War1=tf(kp(i),[0 1]);
War2=tf(kp_Tiz(i),[1 0]);
War3=tf([Td 0],1);
War=War1+War2+War3;
Wcap=Wop/(1+Wop*War);
y=step(Wcap,t)*15;
q=trapz(t,(y).^2);
S(i)=q;
end
Jmin=min(S)
for i=1:length(w),
if S(i)==Jmin
kp_Tizopt=kp_Tiz(i)
kpopt=kp(i)
end
end
Tizopt=kpopt/kp_Tizopt
Td
Td_Tiz=Td/Tizopt
figure(1);
plot(kp,kp_Tiz,'k',kpopt,kp_Tizopt,'*k');grid;
xlabel('kp'); ylabel('kp/Tiz');
figure(2);
plot(kp,S,'k',kpopt,Jmin,'*k'),grid;
xlabel('kp'); ylabel('J');
Результат виконання програми:
kp_Tizopt = 0.0308 kpopt =3.0673
Tizopt = 99.4850 Td =45 Td_Tiz = 0.4523
Td/Tiz= 0.4523;
0 < 0.4523< 0.5 – умова виконується.
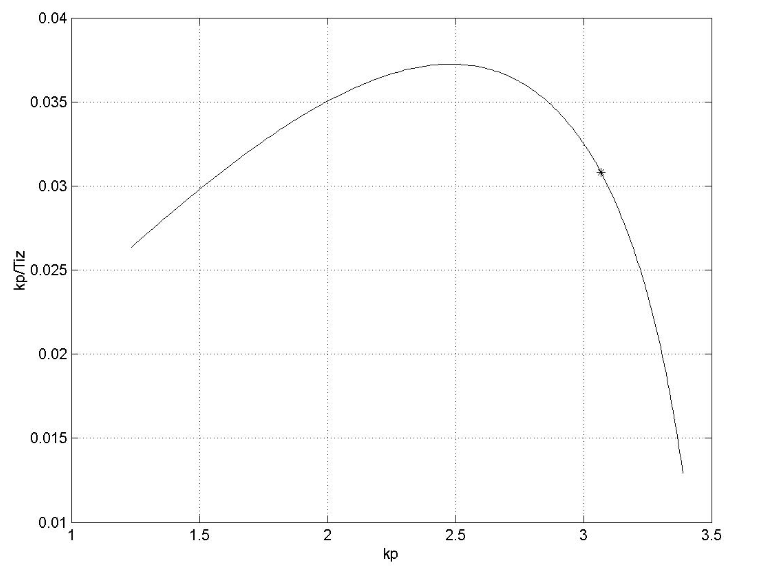
Рис.16 Границя області заданого запасу стійкості САР температури в реакторі з ПІД-регулятором.
Рис.17 Границі залежності між значеннями другої інтегральної оцінки якості J2 і параметром настройки АР Кр
Отже, функція передачі ПІД-регулятора:
