Хід виконання поботи

1. Уточніть завдання до роботи у викладача, щодо дослідження довжин хвиль у спектрі (фіолетової, зеленої, червоної ліній).

2. Установіть на оптичній лаві на одному рівні джерело світла, щілину з міліметровою шкалою і дифракційну решітку.

3. Уключіть лампочку проекційного ліхтаря в мережу змінного струму. Дифракційну решітку установіть перпендикулярно до світлового потоку на такій відстані від щілини, щоб вийшло чітке зображення центральної смуги спектра першого порядку.

4. Виміряйте відстань L від щілини до дифракційної решітки.

5. Для одержання величини h, виміряйте відстань між серединами відповідних смуг спектрів першого порядку і розділіть їх навпіл. Результати вимірів L, h занести в таблиці.

6. Вимірювання виконати 7 разів, згідно пп. 4-5, послідовно пересуваючи щілину на 5 см уздовж оптичної лави.

Методика обробки результатів вимірювання

У виразі (11) змінними величинами є відстань зображення щілини h від осі OD та відстань решітки від щілини L, а шуканою величиною є довжина хвилі . Описану залежність можна представити у вигляді лінійної функції

,

де введено позначення , а довжину хвилі визначити за методом найменших квадратів в Mikrosoft Excel.

Розрахунок довжини хвилі провести за методом найменших квадратів у додатку Excel.

Результати обчислень представити у вигляді

.

Проаналізуйте одержані в роботі результати і висновки запишіть до протоколу.

Контрольні питання

1. Дайте визначення явища дифракції та сформулюйте принцип Гюйгенса - Френеля.

3. Опишіть дифракцію Фраунгофера на щілині та дифракційній решітці.

4. Виведіть формулу для визначення довжини світлової хвилі.

5. Запишіть вираз для лінеаризації рівняння (11).

МАГНІТНЕ ОБЕРТАННЯ ПЛОЩИНИ ПОЛЯРИЗАЦІЇ СВІТЛА

(ЕФЕКТ ФАРАДЕЯ)

Мета роботи

вивчити ефект Фарадея і визначити деякі оптичні й атомні константи речовини на основі аналізу постійної Верде.

Прилади та обладнання

соленоїд із блоком живлення, поляриметр, трубка з досліджуваною речовиною.

Коротка теорія

Природними оптично активними називаються речовини, які обертають площину поляризації плоскої хвилі. Усі оптично неактивні речовини у зовнішньому магнітному полі стають оптично активними. Величина кута повороту площини поляризації , при розповсюдженні світла в напрямку напруженості поля, становить

, (1)

де Н - напруженість магнітного поля, L - довжина оптичного шляху хвилі у речовині, В - коефіцієнт пропорційності, який називається сталою Верде.

Класична теорія явища оптичної активності речовини у магнітному полі виходить із того, що лінійна поляризація може бути представлена лінійною комбінацією двох поляризованих по колу електромагнітних хвиль у протилежних напрямках обертання з амплітудами рівними половині результуючої амплітуди

(2)

та однаковими фазами. Зовнішнє магнітне поле викликає прецесію (рух подібний обертанню дзиги при нахилянні її осі) електронів оптично неактивної речовини. В результаті кутова швидкість обертання векторів амплітуд відрізняється від частоти падаючої хвилі на деяку величину , яка називається ларморівською. У речовині такі циркулярно поляризовані хвилі мають й різні показники заломлення світла, що зумовлює утворення на виході з речовини відмінну від нуля різницю фаз

, (3)

де n_п, n_л - показники заломлення право- та лівополяризованї хвилі відповідно, а _п, _л - кути повороту їхніх амплітуд. При умові , показники заломлення, як функції частоти, можна розкласти в ряд, обмежившись двома доданками, а саме

.

Тепер різницю показників заломлення можна записати у вигляді

. (4)

Додавання таких хвиль на виході з речовини утворює також лінійно поляризовану хвилю з поверненою площиною поляризації відносно падаючої хвилі на кут

. (5)

Порівнюючи (1) та (5), сталу Верде можна записати у вигляді

, (6)

де - фактор дисперсії речовини.

Характерною особливістю ефекту Фарадея є те, що напрямок обертання площини поляризації на виході не змінюється при зміні напрямку вектора напруженості магнітного поля на протилежний.

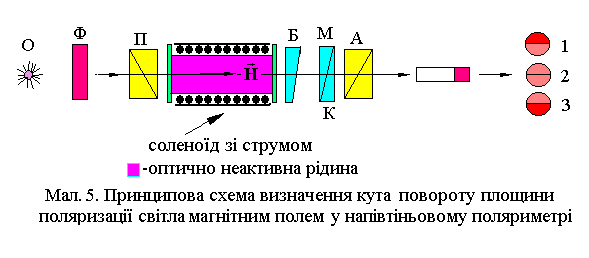
Прилади, за допомогою яких визначають кут повороту площини поляризації, називаються поляриметрами. Існують напівтіньові поляриметри, які забезпечують найбільш точний відлік кута повороту.

Оптична схема напівтіньового поляриметра (у спрощеному виді) показана на Мал.5. Світло від лампи О проходить спочатку через червоний фільтр, що вирізає свтло в околиці частоти . На виході з поляризатора П, світло стає лінійно поляризованим. Воно потрапляє на систему клинового компенсатора, що складається з великого М та малого К кварцових клинів лівого та правого обертання площини поляризації і контрклина Б. У відсутності магнітного поля, клиновий компенсатор та аналізатор А забезпечують дві рівнозатінені області поля трубки спостереження 2. При ввімкненні магнітного поля площина поляризації світла повернеться на кут і поле зору буде мати дві різноосвітлені половинки поля зору 1 або 2. Регулюючи компенсатор можна одержати знову дві рівнозатінені половинки поля зору 2, при цьому на шкалі компенсатора можна визначити кут повороту площини поляризації . Соленоїд вважаємо нескінченно довгим і напруженість магнітного поля Н обчислюємо за формулою , де n – лінійна густина витків, І – величина сили струму у соленоїді.