§ 5. Дифракція Фраунгофера на плоскопаралельній щілині

Дифракція Фраунгофера  дифракція світла в паралельних променях. Нехай паралельний пучок променів світла падає нормально на непрозору площину BG, в якій прорізано плоскопаралельну щілину малої ширини b. Паралельно площині BG (див.Мал.9) розташовано збиральну лінзу Л та екран Е. Збиральною лінзою випромінювання сходиться в точці М фокальної площини, яка суміщена з екраном.

Розрахунок інтерференції від щілини полягає у розбитті вторинного фронту випромінювання на нескінченно малі зони з нескінченно малим зсувом фаз і малими амплітудами і розгляд їх інтерференції, як це зроблено у попередньому параграфі (§ 9).

Для щілини різниця ходу між крайніми променями, що розповсюджуються під кутом до нормалі складає , а різниця фаз

.

В результаті величина амплітуди в точці М становитиме

. (4)

Умовою максимуму амплітуди є

(2)

Розподіл інтенсивності в залежності від подано на малюнку.

§ 6. Дифракція Фраунгофера на дифракційній решітці

Розподіл інтенсивності. Дифракційна решітка утворюється періодичною повторюваністю прозорих (шириною b) та непрозорих плоскопаралельних ділянок (шириною а) на прозорій (наприклад, скляній) поверхні BCG ( див.Мал.10). Величина

d = b + a (1)

називається періодом або сталою решітки. При освітленні решітки світлом, що падає нормально на її поверхню, в напрямку  відбувається інтерференція N п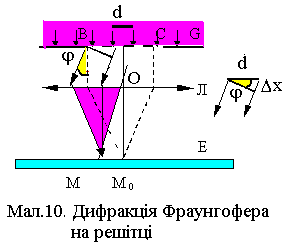 роменів світла від усіх щілин, із сталою величиною зсуву фаз

, (2)

де х  різниця ходу між променями сусідніх прозорих щілин.

Процес інтерференції світла від багатьох прозорих щілин можна описати за допомогою багатопроменевої інтерференції, розглянутої у §8.а). Результуюча амплітуда з урахуванням (2) може бути записати у вигляді

(3)

де  амплітуда хвилі, що утворюється дифракцією від окремої прозорої щілини в напрямку

. (4)

У цьому виразі А₀  амплітуда коливань у точці , при дифракції від однієї щілини у напрямку .

Максимуми виразу (3), що задаються умовою

. (5)

називаються головними. Амплітуда головного максимуму дорівнює

. (6)

В еличина n називається порядком головного максимуму. Головні мінімуми задаються умовою

(7)

Якщо з умови головного максимуму підставити

,

у вираз (3), то амплітуда головного максимуму n-го порядку запишеться у вигляді

. (8)

Головні максимуми розмежовані між собою мінімумами, які задаються умовою

. (9)

Таким чином між двома сусідніми головними максимумами знаходяться (N - 1) мінімум та (N - 2) додаткових максимуми.

На Мал.11 представлено розподіл головних максимумів при різних значеннях числа щілин N в решітці.