1.6.2. Теоретико-вероятностный метод

Практика показывает, что при механической обработке партии деталей на отлаженном оборудовании действительный размер принимает значения, близкие к наладочному размеру. Предельные значения действительного размера маловероятны. При этом возникновение погрешностей обработки подчиняется определенным закономерностям и описывается кривыми или отрезками прямых типа: кривая Гаусса, закон равномерной вероятности, закон Симпсона и др.

Если допустить малую вероятность появления действительного размера, равного предельным значениям замыкающего звена, то можно значительно расширить допуски составляющих размеров, снизить себестоимость изготовления деталей, обеспечив при сборке требуемую точность изделия. На этих положениях и основан вероятностный метод расчета размерных цепей.

Применяя любой метод расчета размерных цепей, следует помнить то, что точность изделий не достигается расчетом и зависит не от метода расчета, а от конкретных условий обработки и сборки, формируется технологической системой при механической обработке и при сборке. Теоретико-вероятностный метод применяют в том случае, если точно найдены закономерности образования погрешностей размеров при обработке партии сопрягаемых деталей.

При вероятностном методе составляющие звенья рассматриваются как случайные величины, а замыкающее звено А_∆ рассматривается также как случайная величина, представляющая сумму известных m + п случайных величин.

Точность замыкающего звена рассматривается как математическое ожидание суммы случайных величин. Следовательно, уже на стадии проектирования допускается определенный процент брака, планируется вероятность получения годных деталей и соединений.

В основе расчетных формул допуска, координат середины поля допуска и предельных отклонений замыкающего звена лежат положения теории вероятности и математической статистики.

Допуск замыкающего звена определяют по следующей зависимости:

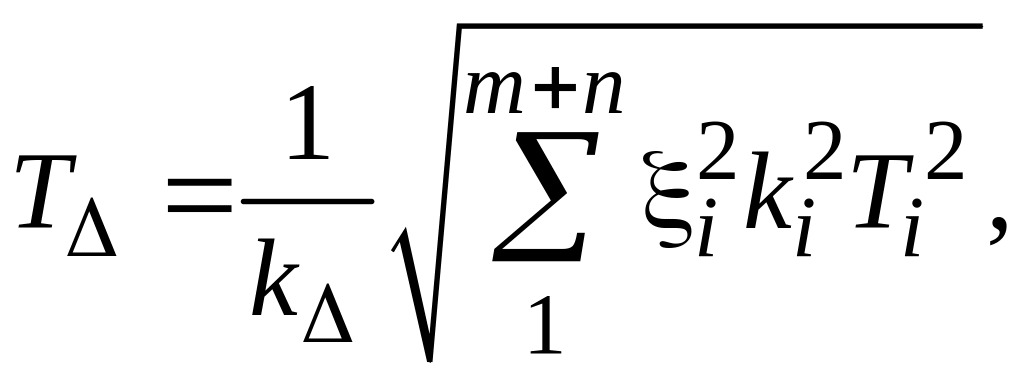(1.13)

где k_∆ и k_i – коэффициенты относительного рассеяния замыкающего и i-го составляющего звена соответственно; ξ_i – передаточное отношение (коэффициент приведения) i-го составляющего звена; T_i – допуск составляющего звена.

При рассеивании значений размера k_∆ исходного звена по закону Гаусса (или близкого к нему) значение коэффициента для каких-либо конкретных условий принимают с учетом процента риска Р выхода размеров в брак:

Р	0,02	0,05	0,10	0,20	0,27	0,50	1,0	1,5	2,0	3,0	4,0	5,0	6,0	8,0	10,0
kΔ	0,81	0,86	0,91	0,97	1,00	1,06	1,16	1,23	1,29	1,38	1,46	1,52	1,6	1,7	1,82

Значение коэффициента k на практике как правило получают опытным путем с последующей математической обработкой результатов измерения деталей выборочной партии. Значения k для различных законов распределения отклонений приведены в работе [9, с. 341].

Значение коэффициента k при обработке присоединительных конических поверхностей вспомогательного инструмента в зависимости от вида поверхности и способа ее получения даны в прил. 10.

Формулу (1.13) расчета допуска замыкающего звена можно записать в следующем виде:

(1.14)

где t_Δ – коэффициент риска, характеризующий вероятность выхода отклонений замыкающего звена за пределы допуска; – коэффициент относительного среднего квадратичного отклонения, характеризующий закон распределения случайных погрешностей составляющих звеньев: – для закона нормального распределения; – для закона Симпсона; – для закона равной вероятности.

При законе нормального распределения отклонений и равновероятном их выходе за обе границы поля допуска значение процента риска Р связано с Ф(t) формулой, %:

P = 100 [ l – Ф(t) ]. (1.15)

Некоторые расчетные коэффициенты t в зависимости от процента риска (при распределении отклонений по закону Гаусса) приведены ниже:

P	0,01	0,1	0,2	0,27	0,5	1,0	2,0	3,0	4,0	5,0	10,0	32,0
t	3,89	3,29	3,12	3,00	2,80	2,57	2,33	2,17	2,06	1,96	1,65	1,00

Считается, что если , то распределение размеров замыкающего звена подчиняется закону нормального распределения независимо от законов распределения составляющих звеньев.

В проектных расчетах, когда законы распределения составляющих звеньев неизвестны, условно принимают распределение всех звеньев одинаковым, соответствующим закону Симпсона (треугольника). Тогда , k_i = 1, 2, а формула для расчета допуска замыкающего звена имеет вид:

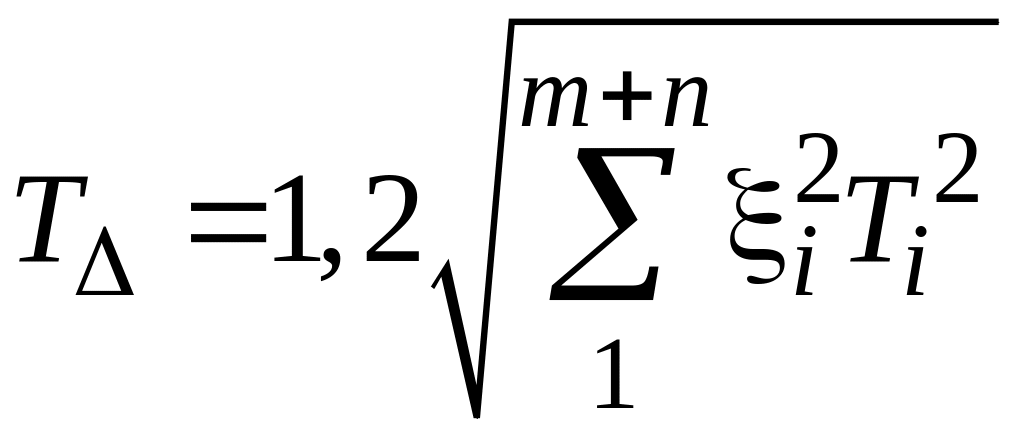. (1.16)

Между k_i, и t имеется следующая зависимость: . По этой формуле при Р = 27 % и t = 3 можно рассчитать коэффициенты k_i для различных законов распределения случайных погрішностей:

для закона Гаусса ;

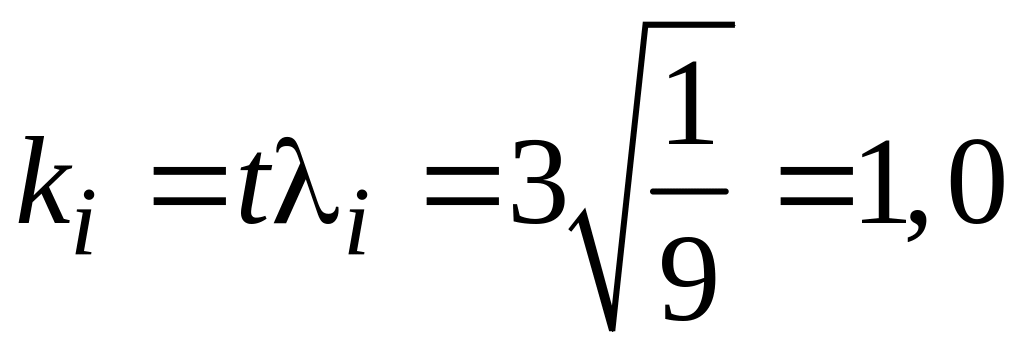для закона Симпсона ;

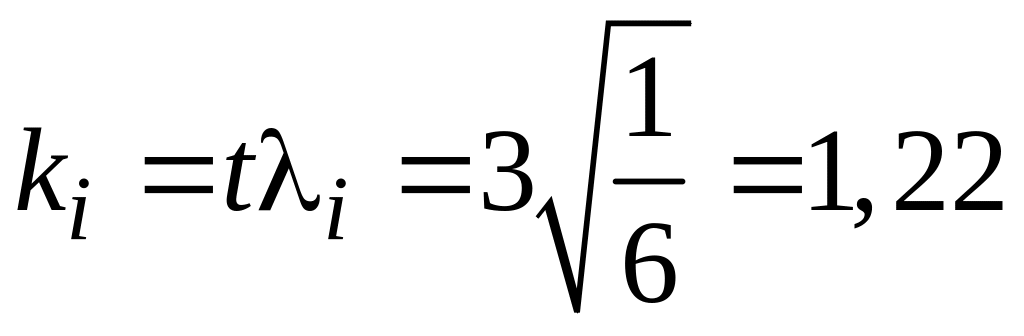для закона равной вероятности .

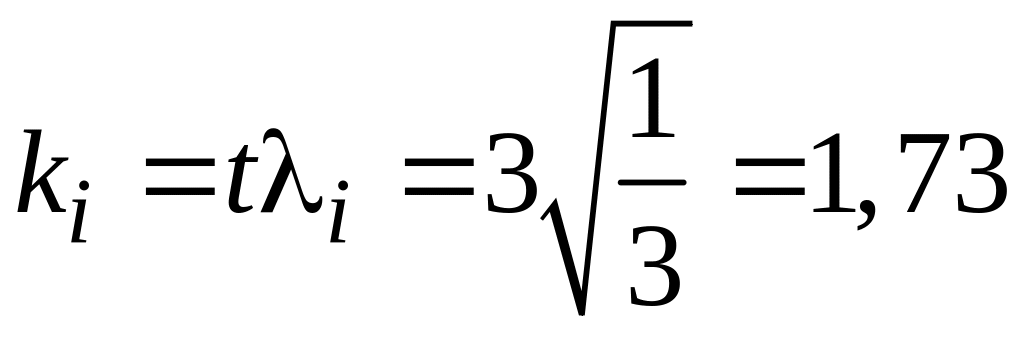Значение λ_i для некоторых законов распределения, а также рекомендации и примеры по определению многозвенных размерных цепей даны в ГОСТ 19415-74.

Если брак составляет 0,27 % и известен коэффициент k_i, то допуск замыкающего звена можно рассчитать по формуле

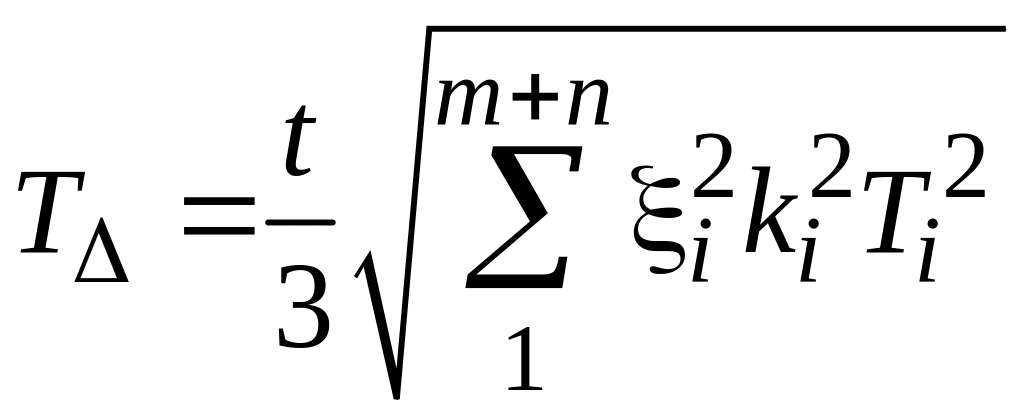. (1.17)

Координату середины поля допуска замыкающего звена устанавливают по формуле

, (1.18)

где ξ_i – передаточное отношение (коэффициент приведения) составляющего звена; и – коэффициенты относительной симметрии i-го составляющего и замыкающего звена соответственно; Т_i – допуск i-го составляющего звена; и – среднее отклонение (координата середины поля допуска) i-го составляющего и замыкающего звеньев соответственно.

На рис. 1.15 приведены параметры замыкающего звена размерной цепи, когда оно рассматривается как сумма независимых случайных величин – проекций составляющих звеньев на направление А_Δ.

Математическое ожидание М_Δ замыкающего звена как случайной величины можно рассчитать по формуле Н. А. Бородачева:

М_Δ = A_Δ + + T_Δ; (1.19)

М_i = A_i + + T_i . (1.20)

Значения коэффициентов k_i , k_Δ , и на практике получают опытным путем с последующей математической обработкой результатов измерений деталей большой партии. В проектных расчетах можно пользоваться средними значениями этих коэффициентов: коэффициент относительного рассеивания для всех размеров k_i = 1, 2; коэффициент относительной асимметрии:

= + 0,1 – для охватываемых поверхностей;

= – 0,1 – для охватывающих поверхностей;

= 0 – для прочих поверхностей.

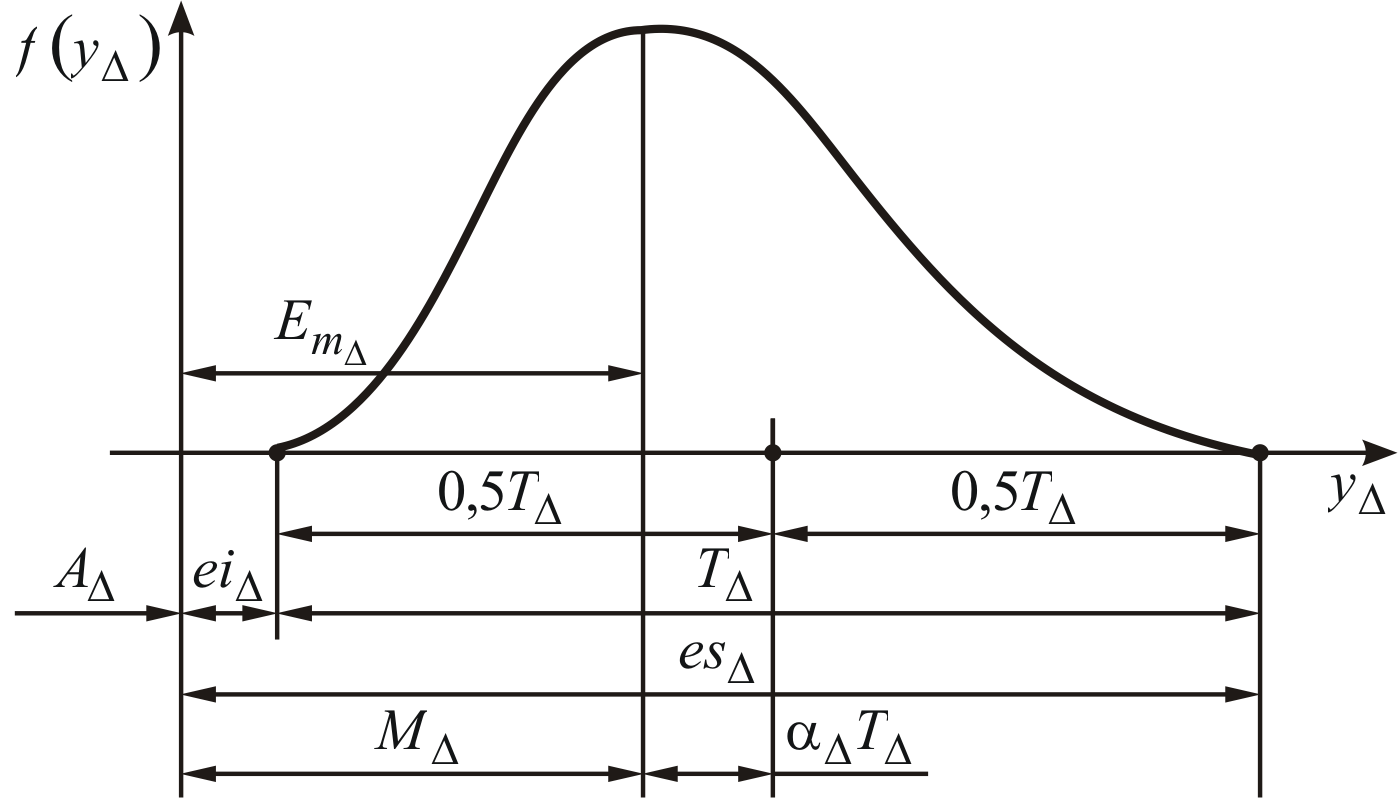
Рисунок 1.15 – График распределения отклонений исходного (замыкающего)

звена: М_Δ – математическое ожидание положения замыкающего звена как случайной

величины

Значения коэффициентов для некоторых законов распределения даны в табл. П1.6. Методы определения точных значений , а также приближенных значений для трехзвенных размерных цепей даны в ГОСТ 19415-74.

Предельные отклонения замыкающего звена при теоретико-вероятностном методе определяют по следующим зависимостям:

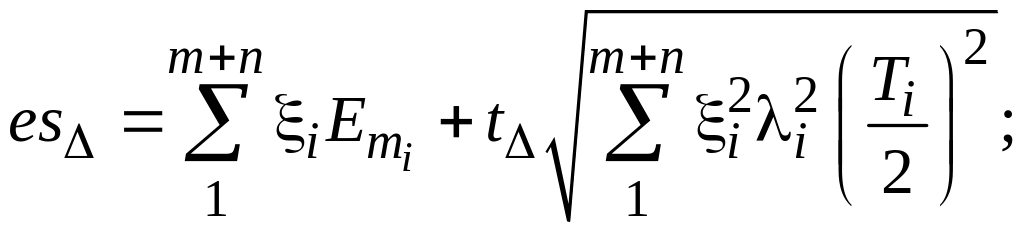(1.21)

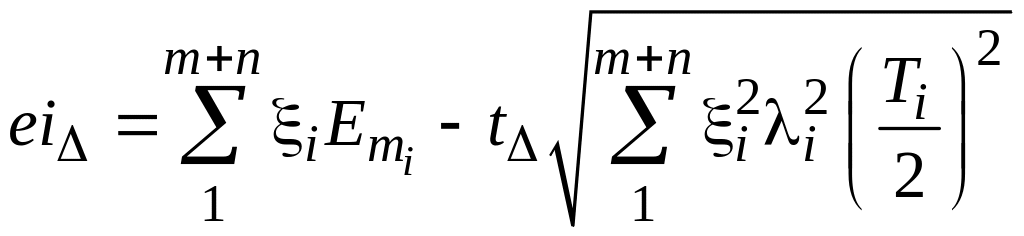. (1.22)

Размерные цепи, для которых риск возможного выхода за пределы поля допуска замыкающих звеньев у части изделий является экономически оправданным, рассчитывают вероятностным методом.