1.5. Задачи, решаемые при расчете размерных цепей

При расчете размерных цепей решаются две задачи: прямая (проектная); обратная (поверочная). Отличаются они входными данными, расчетными параметрами и формулами.

В проектной задаче входными данными являются параметры замыкающего звена: А_Δ, es_Δ, еi_Δ и . Решение проектной задачи сводится к определению параметров составляющих звеньев, которые гарантируют требуемую точность замыкающего звена. Расчетом определяют номинальные размеры , допуски , предельные отклонения , , координаты середины полей допусков всех составляющих звеньев размерной цепи. Индексом m+n обозначено общее количество составляющих звеньев (m – увеличивающих, n – уменьшающих).

Поверочная задача направлена на проверку расчетов, выполненных на стадии проектирования. Входными данными являются параметры составляющих звеньев, полученные в проектных расчетах. При этом определяют параметры замыкающего звена: А_Δ, es_Δ, ei_Δ и Е_Δ, которые должны соответствовать задаче проектирования.

Проектная задача решена правильно, если при решении поверочной задачи параметры замыкающего звена совпадают с этими же параметрами, заданными условиями проектной задачи.

1.6. Методы расчета размерных цепей

Прямая и обратная задачи могут быть решены двумя методами: максимума-минимума (max-min) или теоретико-вероятностным. Каждый из этих методов имеет свое содержание и свою область применения.

1.6.1. Метод max-min

В основе метода max-min лежит предположение о том, что действительный размер детали при механической обработке принимает предельные значения D_max (d_max) или D_min (d_min), а при сборке имеет место их неблагоприятное сочетание: наибольший вал (d_max) собирается с наименьшим отверстием (D_min) и – наоборот. При таком предположении все детали будут годными, так как выполняются условия годности деталей: вала (d_max ≥ d_д ≥ d_min) и отверстия (d_max ≥ d_д ≥ d_min). Допуски, рассчитанные по методу max-min, гарантируют полную взаимозаменяемость деталей при сборке.

Метод max-min устанавливает следующие формулы расчета параметра замыкающего звена:

• номинальный размер

; (1.3)

• допуск

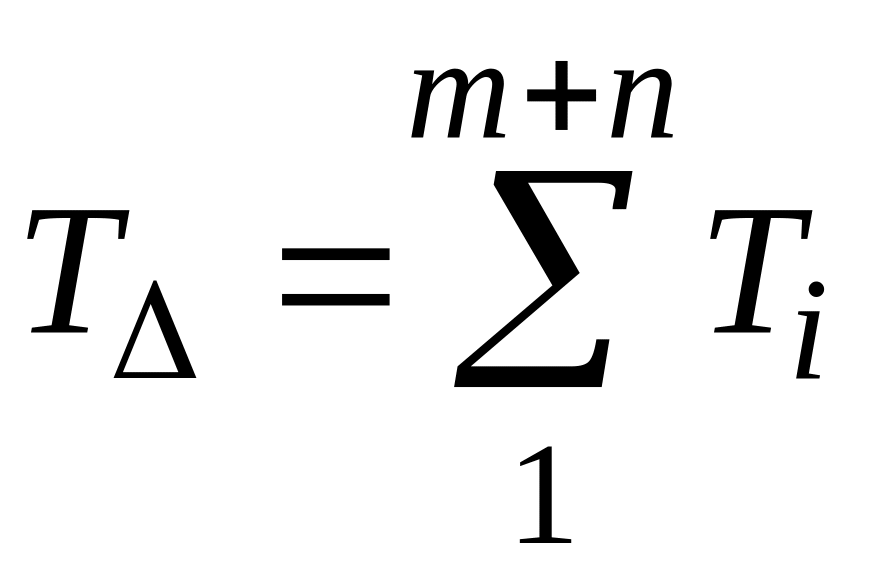; (1.4)

• предельные отклонения

(1.5)

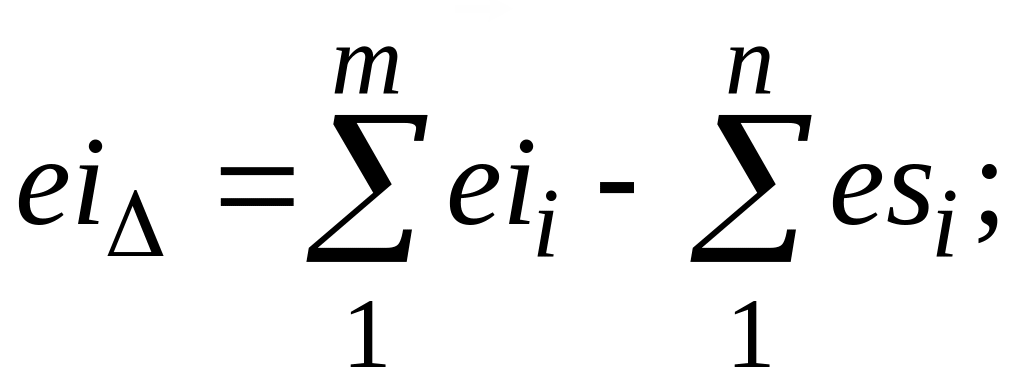(1.6)

• координата середины поля допуска

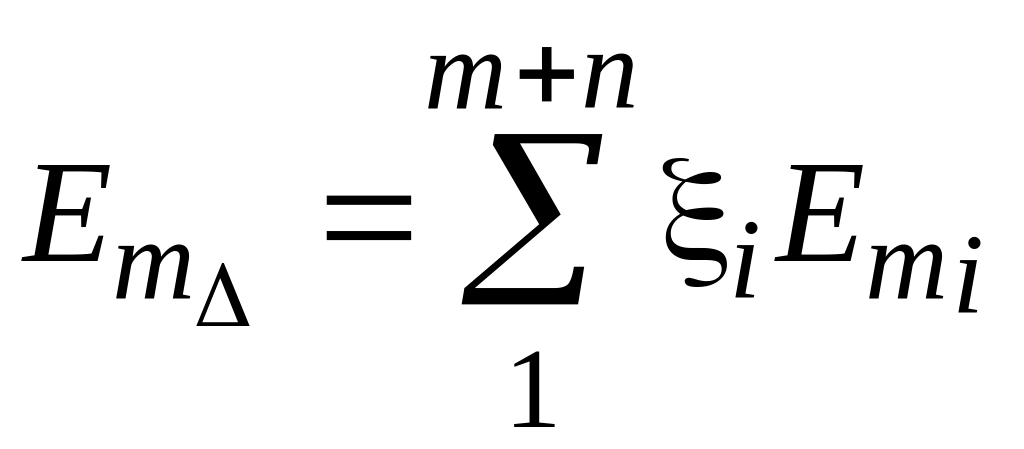, (1.7)

где es_i, ei_i – верхнее и нижнее предельные отклонения составляющих звеньев; m и n – число увеличивающихся и уменьшающихся звеньев соответственно; ξ_i – передаточное отношение: ξ_i = +1 – для увеличивающихся звеньев; ξ_i = –1 – для уменьшающихся звеньев; – координата середины поля допуска составляющих звеньев, которая может быть рассчитана по формулам:

(1.8)

(1.9)

(1.10)

Главная особенность метода max-min состоит в том, что допуск замыкающего звена равен сумме допусков составляющих звеньев (форму- ла (1.4)). Это указывает на тот факт, что если допуск замыкающего звена мал, а количество составляющих звеньев велико, то допуск каждого составляющего звена должен составлять определенную долю от допуска замыкающего звена. Эта доля может быть настолько мала, что ее невозможно обеспечить известными методами механической обработки, а если и возможно, то это экономически нецелесообразно. Поэтому метод max-min применяют для малозвенных размерных цепей типа «вал–втулка», «шпонка–паз» на валу или во втулке и т. п. Метод max-min применяют при расчете двух- трёхзвенных размерных цепей с высокой точностью замыкающего звена и многозвенных размерных цепей с малой точностью замыкающего звена.

Достоинством метода max-min является то, что он гарантирует полную взаимозаменяемость при первоначальной сборке и при ремонте изделий.

Целесообразность применения метода max-min можно проверить следующим анализом размерной цепи.

По номинальным размерам составляющих звеньев размерной цепи определяют их среднее значение:

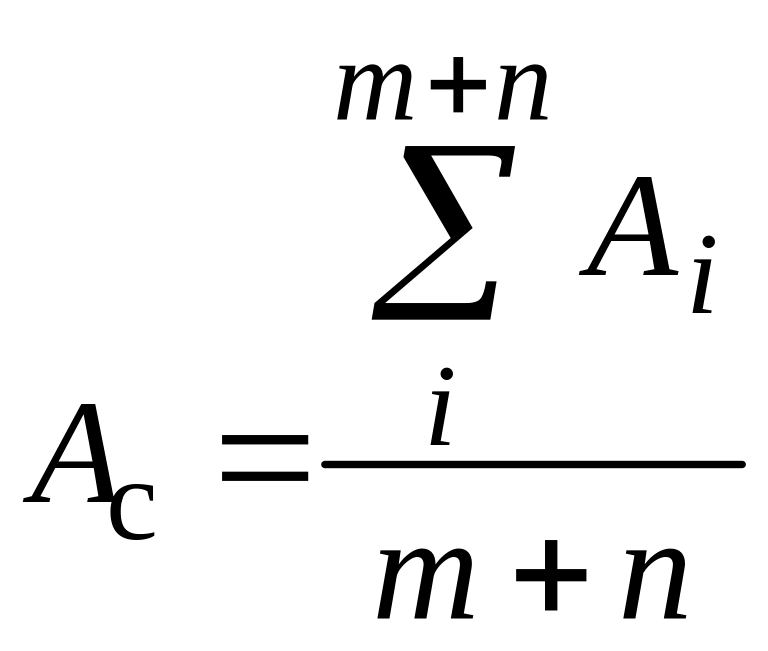. (1.11)

Затем по определенному допуску на размер замыкающего звена Т_∆ и числу составляющих звеньев определяют среднее значение допуска для каждого звена:

. (1.12)

По полученным значениям А_c и Т_c определяют ближайший квалитет по ГОСТ 25346-89, табл. 6. Затем делают следующие выводы:

1. Если m + n < 3, а квалитет 6–8, то целесообразно принять метод max-min, так как снижение трудоемкости сборки окупит повышение стоимости механической обработки.

2. Если при Т_c получается 9-й квалитет и выше, то можно принять метод max-min при 3 < m + n < 5.

3. Если m + n > 5, а квалитет менее 8–9, то рекомендуется обратиться к поиску других методов достижения точности замыкающего звена.

Метод max-min можно применить также и при точности сопрягаемых деталей в пределах 4–5-го квалитетов, если это целесообразно с точки зрения необходимости создания высокоточных взаимозаменяемых соединений, сконструированных по агрегатно-модульному принципу.

В размерных цепях, в которых должна быть обеспечена полная взаимозаменяемость, допуски рассчитывают только по методу максимума-минимума.