1.7. Способы решения проектной задачи

Особенность решения проектной задачи методом полной или неполной взаимозаменяемости состоит в том, что связь между допуском замыкающего звена Т_Δ и допусками Т_i составляющих звеньев устанавливается только одним из уравнений (1.4) или (1.14), в то время, как количество неизвестных в размерной цепи составляет (m + n). На практике уравнения (1.4) или (1.14) решают одним из следующих способов:

1) подбора (попыток или пробных расчетов);

2) равных допусков;

3) одинакового квалитета;

4) экономического обоснования допуска.

Способ пробных расчетов состоит в том, что конструктор назначает допуски составляющих звеньев с учетом требуемой точности размеров и расположения поверхностей и сложности выполнения размеров, а затем решает уравнение (формула (1.4) – метод max-min или формула (1.14) – вероятностный метод). Если условия (1.4) или (1.14) не выполняются, то конструктор вносит изменения на чертеже, уменьшая или увеличивая допуски размеров, которые на его усмотрение можно изменить. Решение задачи носит субъективный характер. Этот способ распространен на производстве, однако он может быть связан с назначением нестандартных допусков.

Способ равных допусков применяют в том случае, когда номинальные размеры составляющих звеньев размерной цепи находятся в одном интервале размеров по стандарту. Распределение допуска замыкающего звена между составляющими звеньями выполняют по формулам (1.12), (1.23) или (1.24):

для метода max-min – ;

для теоретико-вероятностного метода – 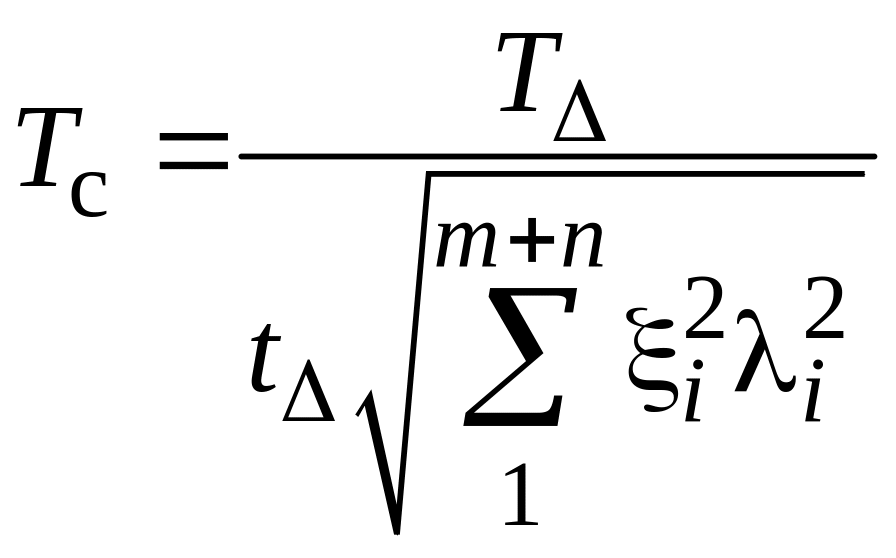. (1.23)

Значения средних допусков на составляющие звенья при расчете размерных цепей вероятностным методом (Р = 0,27 %, λ_i = 0,4) можно определить по табл. П1.5 или по упрощенной формуле

, (1.24)

где λ_c – среднее значение коэффициентов относительного рассеивания составляющих звеньев.

Способ одинакового квалитета сводится к расчету квалитета, в котором назначают допуски составляющих звеньев размерной цепи. Квалитет выбирают по ГОСТ 25346-82 по величине a_c, которую рассчитывают в зависимости от метода расчета размерных цепей:

при методе max-min 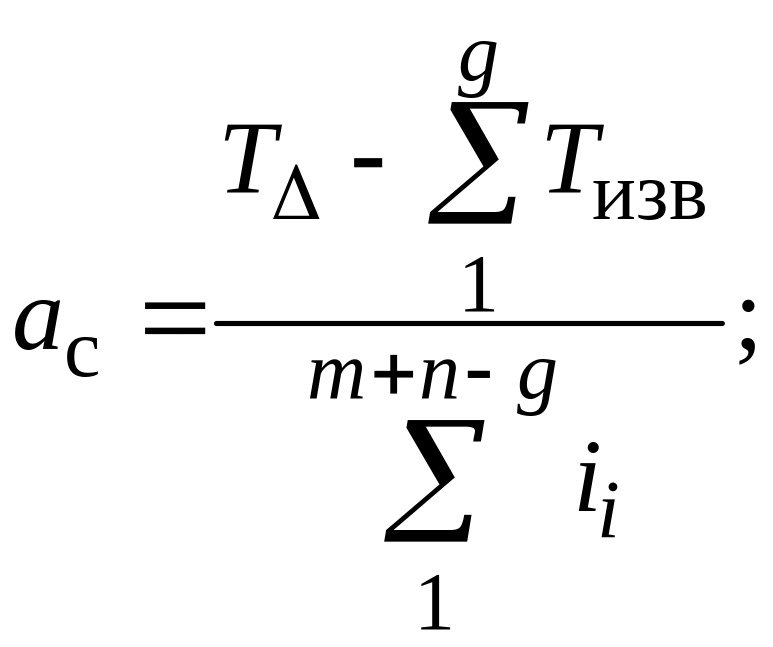(1.25)

при теоретико-вероятностном методе 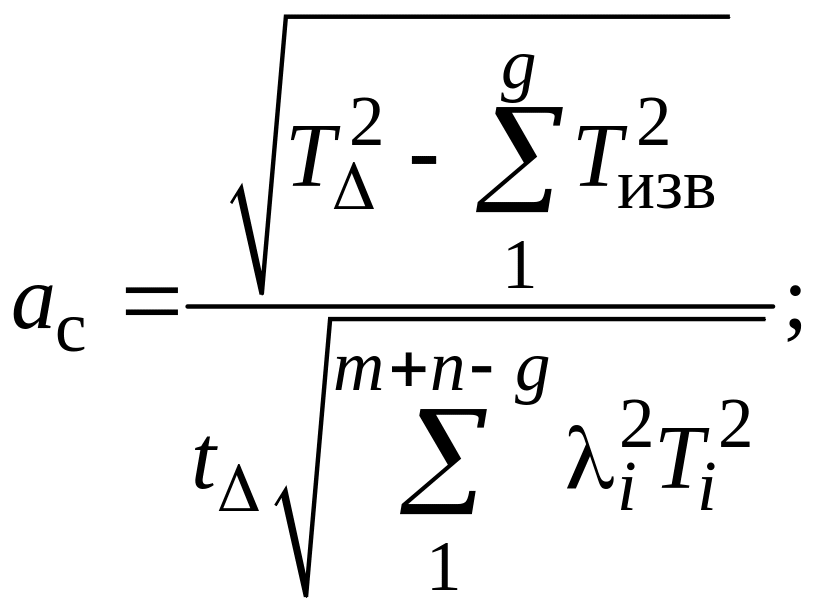(1.26)

или по упрощенной формуле 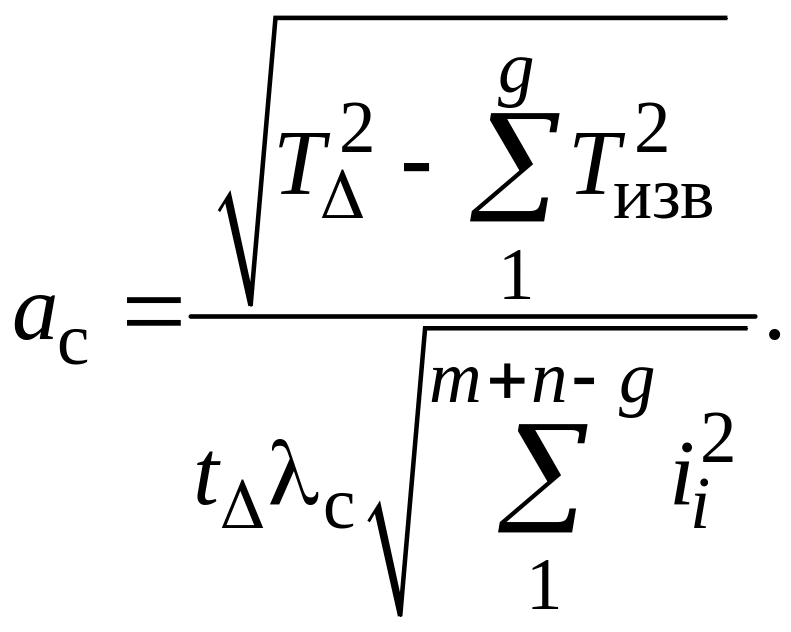(1.27)

При Гауссовом законе распределения погрешностей размера и проценте риска Р = 0,27 % коэффициенты t и λ: t_Δ = 3; . Тогда формула (1.24) имеет вид:

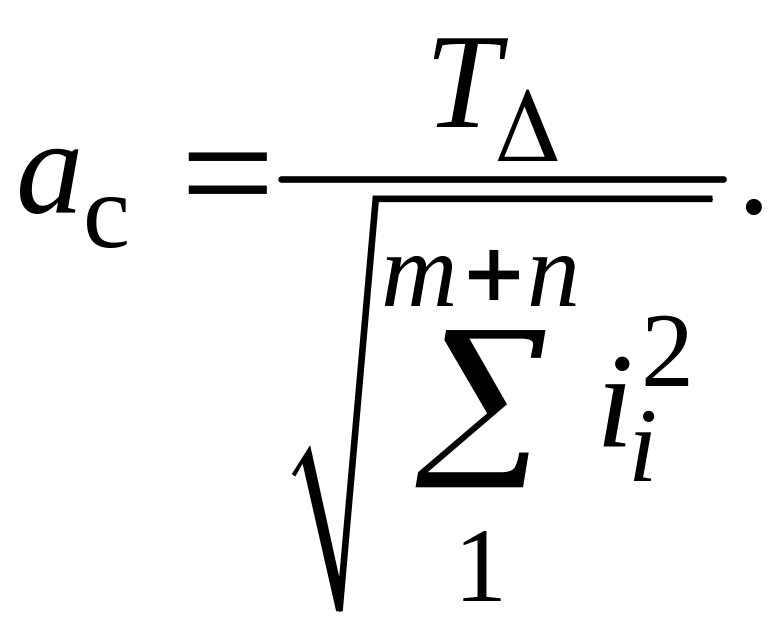(1.28)

При расчете размерных цепей способом одинакового квалитета имеются особенности, связанные с тем, что среднее расчетное количество единиц допуска а_c, как правило, не совпадает со стандартным значением а (табл. П1.3), т.е.

а_c ≠ a,

где а_c – расчетное количество единиц допуска; а – стандартное количество единиц допуска по ГОСТ 25346-82.

В тех случаях, когда а_c ≠ a допуски, назначенные по стандарту, не обеспечивают условие (1.4). Поэтому одно из составляющих звеньев условно принимают за корректирующее, и допуск на него принимают не стандартный, а рассчитывают из условий (1.4) или (1.14):

Т_∆ = T₁ + Т₂ + Т₃ +... + Т_кор +... + Т_m+n – (метод max-min);

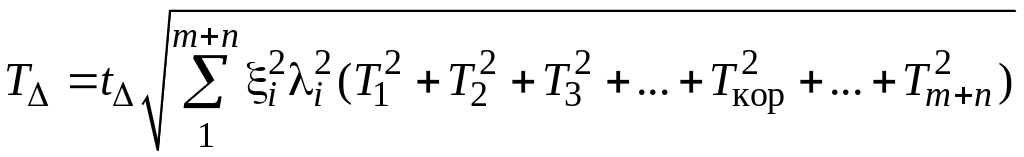– (теоретико-вероятностный метод).

Из этих двух условий можно получить формулы для расчета допуска корректирующего звена:

при методе max-min 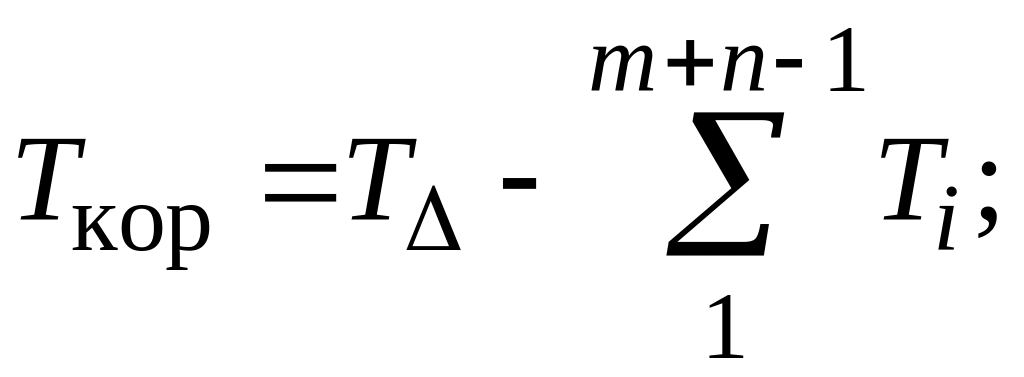(1.29)

при теоретико-вероятностном методе

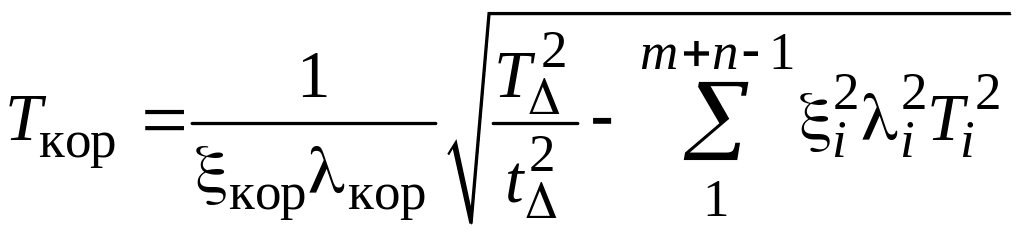, (1.30)

где Т_i – допуски составляющих звеньев, назначенные по табл. П1.3 в зависимости от номинального размера звеньев и принятого квалитета.

При Гауссовом законе распределения отклонений размера и проценте риска Р = 0,27 % коэффициенты t и λ: t_Δ =3; . Тогда формула (1.30) имеет упрощенный вид:

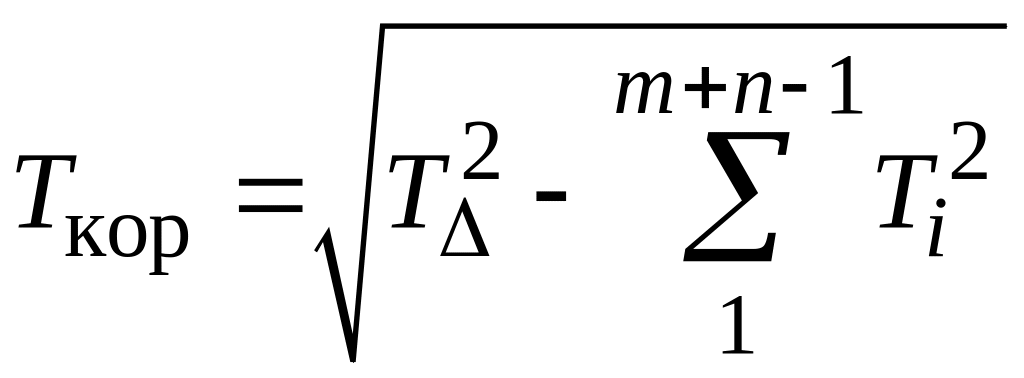. (1.31)

В качестве корректирующего звена рекомендуется принимать одно из самых больших по величине и менее ответственных составляющих звеньев в размерной цепи.

Следующим этапом решения проектной задачи способом одинакового квалитета является назначение предельных отклонений на составляющие звенья, кроме корректирующего звена.

При назначении предельных отклонений рекомендуется составляющие размеры (звенья) разбить на три группы:

• охватывающие поверхности;

• охватываемые поверхности;

• смешанные (уступов, впадин и т. п.).

Предельные отклонения первых двух групп принимают равными допуску на изготовление: со знаком «плюс» – для охватывающих поверхностей как на основное отверстие, со знаком «минус» – для охватываемых повехностей как на основной вал. Таким образом, для этих двух групп размеров допуск задают в обрабатываемый материал. Для третьей группы размеров предельные отклонения назначают в зависимости от технологии обработки поверхности (как на вал или как на отверстие). Допускается назначение симметричных предельных отклонений.

Предельные отклонения корректирующего звена рассчитывают в такой последовательности:

1. Рассчитать координаты середин полей допусков составляющих звеньев по формуле (1.10):

.

2. Рассчитать координаты середин полей допусков корректирующего звена:

. (1.32)

3. Рассчитать предельные отклонения корректирующего звена:

; (1.33)

. (1.34)

По результатам расчета предельных размеров на чертеже детали проставляют исполнительные размеры составляющих звеньев.

Способ экономического обоснования допусков состоит в том, что стоимость выполнения операций зависит от допуска на размер обрабатываемой поверхности. Следовательно, из многих вариантов технологических процессов, вариантов простановки размеров на чертежах и допусков на размеры путем расчета можно найти такой вариант, при котором стоимость изготовления деталей в изделии является наименьшей. Задача сводится к определению таких значений допусков, чтобы стоимость изготовления всех деталей изделия была наименьшей, а изделие могло выполнять свои функциональные свойства с заданной точностью и надежностью.

Метод экономического обоснования допусков – достаточно сложный и трудоемкий. Кроме того, технологический процесс должен быть реализован однозначно в соответствии с выполненными расчетами. Это возможно в условиях крупносерийного и массового производства с высоким уровнем автоматизации и надежности технологических процессов. Метод предполагает наличие банка данных для расчета себестоимости при конкретных условиях обработки и сборки изделий. Однако он применяется редко из-за сложности и трудоемкости.