5. Модель ситуаційної системи керування гальмівною позицією на спускній частині гірки в середовищи MatLab 6.5

При проектуванні інтелектуальних систем управління усе більш широке практичне застосування знаходять методи ситуаційного керування [1-11].

Сутність ситуаційного керування полягає в наступному [7]. При синтезі системи вирішується завдання класифікації – розбивки множини можливих ситуацій на класи-еталони й зіставлення кожного еталону керуючого рішення. На етапі керування в реальному часі вирішується завдання ідентифікації – модель поточної ситуації зіставляється з еталонами й приймається керування, приписане тому еталону, що зіставимо з поточною ситуацією. Головним завданням розробки ситуаційного керування є вибір моделі подання ситуації. Модель визначає апарат теорії аналізу й синтезу ситуаційних систем керування. Універсальним апаратом подання моделі ситуацій (поточний і еталонний) є нечіткі множини.

Головною перевагою представлення моделі ситуацій нечіткими множинами є можливість у рамках єдиного апарата описувати складні гібридні системи, модель ситуації яких відбиває як дискретні, так і безперервні за значенням параметри; чітко виміряні й нечітко сформовані факти, а також різні динамічні властивості об'єкта.

Постановка задачі

До основних завдань, що повинна виконувати система регулювання швидкістю скочування: забезпечення необхідної дальності пробігу відчепів при безпечній швидкості зіткнення їх з вагонами, що знаходяться на підгіркових коліях (прицільне регулювання); створення необхідного інтервалу між відчепами, що скочуються на спускній частині гірки (інтервальне регулювання).

Для вирішення задачі управління швидкістю відчепів на сортувальних гірках використовуються три гальмівні позиції (Рисунок 1) [3]:

I ГП (верхня) – розташована на швидкісному уклоні у головній частині гірки, до першої розділової стрілки; на цій ГП відбувається інтервальне регулювання.

ІІ ГП (пучкова) – розташована на швидкісному уклоні перед розділовою стрілкою кожного пучка колій; тут відбувається інтервальне і прицільне гальмування.

ІІІ ГП (паркова) – на початку кожної сортувальної колії для прицільного гальмування.

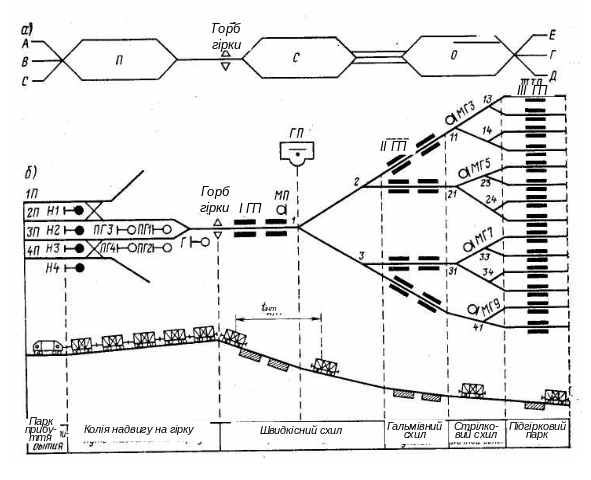
Рисунок 1 – Структурна схема розташування гальмівних позицій на гірці.

Поставимо задачу розробки ситуаційної системи управління першою гальмівною позицією (І ГП), що забезпечує інтервальне регулювання швидкості скочування відчепів на спускній частині гірки.

До величин, що впливають на процес керування скочуванням відчепів на першій гальмівній позиції відносяться: вагова категорія відчепа, швидкість руху і відстань до наступного та попереднього відчепів.

Розробка нечіткої моделі

Основною стадією в розробці ситуаційної системи регулювання швидкості скочування відчепів є створення нечіткої моделі з використанням основних етапів нечіткого висновку [8-11].

Розробити ситуаційну систему керування І ГП на спускній частині гірки. До вхідних параметрів системи нечіткого висновку належать наступні лінгвістичні змінні:

• „ВАГА” – вагова категорія відчепа, позначимо її як ₁, терм-множиною ₁ є спрощена множина Т₁={Легка, Середня, Важка}, або в скороченому варіанті Т₁={Л, С, В};

• „ШВИДКІСТЬ” – швидкість руху відчепа – ₂, з терм-множиною Т₂={Не рухається, Мала, Середня, Велика}, або у скороченому вигляді Т₂={НР, М, С, В};

• „ВІДСТАНЬ” – відстань до попереднього відчепу – ₃, значення якої визначаються множиною Т₃={Мала, Середня, Велика}, або у скороченому вигляді Т₃={М, С, В}. Слід зазначити, що якщо попереду відчепа нема інших відчепів, то „ВІДСТАНЬ” приймається великою;

До вихідних параметрів системи нечіткого висновку відноситься єдина лінгвістична змінна – „СТУПІНЬ ГАЛЬМУВАННЯ” – ступінь гальмування уповільнювача, позначимо її як ₁. Змінна ₁ визначається наступною терм-множиною: Т={Не гальмувати, І ступінь, ІІ ступінь, ІІІ ступінь. IV ступінь}, або у скороченому вигляді Т={НГ, І ст, ІІ ст, ІІІ ст, IV ст}.

Слід зазначити, що ситуаційна система буде створена із застосуванням алгоритму нечіткого висновку Мамдані [6].

База правил на основі якої відбувається керування І ГП буде мати вигляд:

ПРАВИЛО_1: ЯКЩО „₂НР” , ТО „₁НГ”

*

*

*

*

*

*

*

*

ПРАВИЛО_15: ЯКЩО „₁В” І „₂В” І „₃С”, ТО „₁ІІІ ст”

Після розробки бази правил перейти безпосередньо до нечіткого моделювання процесу регулювання швидкістю. Розробку будемо проводити за допомогою інтегрованої середи розробок MatLab 6.5 та пакету Fuzzy Logic ToolBox призначеного для реалізації процесу нечіткого моделювання [2].

На першому етапі синтезуємо нечітку модель системи курування І ГП, на основі розробленої бази правил.

Процес розробки системи нечіткого висновку в інтерактивному режимі для моделі регулювання швидкості відчепа на І ГП складається у виконанні наступної послідовності дій:

Викликаємо редактор систем нечіткого висновку FIS, для чого у вікні команд набрати ім'я відповідної функції fuzzy [1]. Оскільки на вхід системи для управління І ГП подається три параметри, то необхідно додати в розроблювальну систему FIS ще дві вхідну змінну.

Змінимо імена вхідною змінною, запропонованою системою MATLAB за замовчуванням. Результат додавання і зміни імен змінних системи нечіткого висновку зображений на рисунку 2.

На вихід системи нечіткого висновку подається одна змінна – „СТУПІНЬ ГАЛЬМУВАННЯ”, тому нема необхідності змінювати кількість вихідних параметрів, змінимо тільки назву.

Із-за некоректного відображення символів кирилиці лінгвістичні змінні будемо називати словами англійської мови, так „ВАГА” описується як „Weight”, „ШВИДКІСТЬ” – „Speed”, „ВІДСТАНЬ” – „Distance”, „СТУПІНЬ ГАЛЬМУВАННЯ” – „Level”.

Тепер необхідно визначити терми і їхні функції приналежності для вхідної й вихідної змінних системи нечіткого висновку. Для цієї мети варто скористатися редактором функцій приналежності, що може бути викликаний в наступний способів: Edit > Membership Functions…

Після виклику редактора функцій приналежності кожної зі змінних за замовчуванням пропонується 3 терми із трикутними функції приналежності.

Далі змінимо назви термів першої вхідний змінної “Weight”, запропоновані системою MATLAB за замовчуванням на “Light”, “Middle”, “Heavy” відповідно кирилицею „Легка”, „Середня”, „Важка”. Після чого змінимо тип функцій приналежності першої змінної, запропонований за замовчуванням, на функції типу трапеція – „trapmf”, вибравши відповідний пункт у поле Type. В поля Range і Display Range заносимо діапазон значень вхідної змінної „Weight” він дорівнює [0 120]. Для функцій приналежності кожного терму замінимо параметри (поле Params) наступим чином: для терму “Light” задамо параметри [0 0 20 40], для терму “Middle” – [20 40 60 80] і для тему “Heavy” – [60 80 200 200]. Слід зазначити, що вхідна величина „ВАГА” дорівнює натиску колеса відчепа на рейку і вимірюється у кН.

Для другої вхідної лінгвістичної змінної „Speed” („ШВИДКІСТЬ”) змінимо запропоновану системою кількість термів три на чотири за допомогою команди Edit>Add Custom MF. Змінимо назви термів другий вхідний змінної „Speed” на “Stop”, “Small”, “Middle”, “Large” відповідно, або українською „Не рухається”, „Мала”, „Середня”, „Велика”. Значення інших полів наступні:

• Range і Display Range: [0 30];

• поле Type для терму “Large”: trapmf;

• поле Type для інших термів: trimf;

• параметри термів (поле Params): “Stop” – [0 0 7] , “Small” – [0 7 14], “Middle” – [7 14 21] , “Large” – [14 21 30 30];

Слід зазначити, що вхідна фізичка величина „ШВИДКІСТЬ” вимірюється у км/год.

Змінимо назви термів третьої вхідний змінної „Distance” („ВІДСТАНЬ”) на “Small”, “Middle”, “Large” відповідно, або українською „Мала”, „Середня”, „Велика”. Значення інших полів наступні:

• Range і Display Range: [0 200];

• поле Type для термів “Small” та “Large” : trapmf;

• поле Type для терму “Middle”: trimf;

• параметри термів (поле Params): “Small” – [0 0 50 100], , “Middle” – [50 100 150], “Large” – [100 150 1000 1000];

Слід зазначити, що вхідна величина „ВІДСТАНЬ” вимірюється у метрах.

Після обробки вхідних змінних перейдемо до завдання функцій приналежності термів вихідної змінної „СТУПІНЬ ГЛЬМУВАННЯ” (“Level”).

Для вихідної лінгвістичної змінної „Level” змінимо запропоновану системою кількість термів три на пять за допомогою команди Edit>Add Custom MF…

Змінимо назви термів третьої вихідний змінної „Level” на “L0”, “L1”, “L2”, “L3”, “L4” відповідно, або в символах кирилиці „Не гальмувати”, „І ступінь”, „ІІ ступінь”, „ІІІ ступінь”, „IV ступінь”. Для змінної всіх термів змінної „Level” тип функції приналежності залишимо незмінним – trimf (трикутна). В поля Range і Display Range заносимо діапазон значень вхідної змінної „Level” він дорівнює [0 1000]. Змінимо параметри термів вихідної змінної на наступні значення: “L0” – [0 0 170], “L1” – [0 170 340], “L2” – [170 340 510], “L3” – [340 510 680], “L4” – [510 680 850]. Слід зазначити, що вхідна величина „СТУПІНЬ ГЛЬМУВАННЯ” дорівнює тиску у гальмівному циліндрі уповільнювача і вимірюється у кПа.

Перейдемо тепер до визначення правила нечіткого висновку для розроблювальної експертної системи. Для цієї мети варто скористатися редактором правил, що може бути викликаний у наступний способів: командою меню Edit>Rules...

Оскільки спочатку база правил нечіткого висновку порожня, то після виклику редактора правил центральне багатострокове поле уведення не містить ніяких правил. Для їхнього визначення варто використати поля меню й перемикачі в нижній частині графічного інтерфейсу редактори правил. Для завдання першого правила варто залишити виділене за замовчуванням поле з ім'ям терму “Light” для першої вхідний змінної, поле з ім'ям “Middle” для другий вхідний змінної, поле з ім'ям терму “Small” для третьої вхідної змінної а також поле з ім'ям терму „L1” для вихідної змінної. Далі треба перемикач Connection поставити в положення AND (логічне І) і нажати на кнопку Add rule. Після цього перше правило із символами кирилиці відобразиться у верхнім вікні.

Аналогічним чином вводимо усі правила з бази правил нечітких продукцій для І ГП.

Вид редактора правил після їхнього визначення для розроблювальної ситуаційної системи зображений на рисунку 4

Після завдання правил нечіткого висновку виявляється можливим одержати результат нечіткого висновку (значення вихідний змінної) для конкретних значень вхідних змінних. Із цією метою необхідно відкрити програму перегляду правил одним наступним способом: меню View> Rules

Після виклику програми перегляду правил для системи нечіткого висновку за замовчуванням для вхідних змінних запропоновані середні значення з інтервалу їхніх припустимих значень. На рисунку 5 приведено результати нечіткого висновку для ситуації при якій на І ГП входить відчеп колеса на рейку якого становить 60 кН, швидкість відчепа 15 км/год, відстанню до попереднього відчепа 100 м. При такій ситуації результатом нечіткого висновку буде значення тиску у гальмівному балоні уповільнювача на першій гальмівній позиції буде дорівнювати 201 кПа.

В аналогічний спосіб можна підрахувати значення тиску у гальмівному балоні для будь-якого значення вхідних параметрів.

Головною перевагою представлення моделі ситуацій нечіткими множинами є можливість у рамках єдиного апарата описувати складні гібридні системи, модель ситуації яких відбиває як дискретні, так і безперервні за значенням параметри; чітко виміряні й нечітко сформовані факти, а також різні динамічні властивості об'єкта.

Найбільш ефективний цей спосіб виявляється для складних нечітких моделей з більшим числом змінних і правил нечіткого уведення. У цьому випадку завдання змінних і функцій приналежності їх термів у графічному режимі, а також візуалізація правил дозволяють істотно зменшити трудомісткість розробки нечіткої моделі, знизити кількість можливих помилок і скоротити загальний час нечіткого моделювання.

Результати нечіткого моделювання та розробки синтезу системи можна застосовувати при створенні нечітких контролерів для керування ситуаційної системи управління скочуванням відчепу на гірці.

Список використаних джерел по п.4.5.

1. Гультяев А. Візуальне моделювання в середовищі MATLAB: навчальний курс. Спб: Питер, 2000. 432 с.

2. Дияконів В., Круглов В. Математичні пакети розширення MATLAB. Спеціальний довідник. - Спб: Питер, 2001. - 480 с

3. Казаков А. А., Бубнов В. Д., Казаков Е. А. Станционные устрой­ства автоматики и телемеханики: Учебник для техникумов ж.-д. трансп. М.: Транспорт, 1990.—431 с.

4. Микропроцессорные информационно-управляющие системы автоматизации сортировочных процессов. Учебное пособие. Иванченко В.Н, Ростов н/Д, РИИЖГ,- 1984.

5. Нечіткі безлічі в моделях керування й штучного інтелекту. /Під ред. Д.А. Поспєлова.-М.: Наука, 1986.-312с.

6. Орловський С.А. Проблеми прийняття рішень при нечіткій вихідній інформації. -М.:Наука,1981. -208с.

7. Поспєлов Д.А. Ситуаційне керування: теорія й практика. -М.: Наука, 1986. -288с.

8. Прикладні нечіткі системи // Під. ред. Т.Терано, К.Асаи. (М.: Мир,1993. -368с.

9. Каргин А.А., Петренко Т.Г. Интеллектуальные машины: от нечетких регуляторов до ситуационных систем управления // Вестник Донецкого государственного университета. Серия А, Донецк, ДонГУ, 1998.-N2. -с.164-172.

10. ПАНЧЕНКО С.В., СЫТНИК В.Б., ЯЦЬКО С.И. Моделирование адаптивных дискретных систем. Оптимизация параметров управляющих импульсных последовательностей нечетких регуляторов. Інформаційно-керуючі системи на залізничному транспорті. – Харків: УкрДАЗТ, № 5,6, 2006, с.52 - 62.

11. Сытник Б.Т. Организация базы знаний в ИУС реального времени ГЭТ //ИУСЖТ, № 6, 1998. –С. 51-53.

ПРИЛОЖЕНИЕ

(Образец оформления раздела анализ системы)