Администрация городского округа Самары

САМАРСКИЙ МУНИЦИПАЛЬНЫЙ ИНСТИТУТ УПРАВЛЕНИЯ

Кафедра математических методов и информационных технологий

Учебно-методический комплекс по дисциплине

«ЭМММ»

ЛЕКЦИОННЫЕ МАТЕРИАЛЫ

САМАРА – 2007 г.

Содержание

1. Основные понятия исследования операций.

2. Геометрическая интерпретация задач оптимизации.

3. Задача линейного программирования. Симплекс – метод

4. Двойственные задачи

5. Целочисленное программирование

6. Транспортная задача

7. Транспортная задача на сети

8. Динамическое программирование

9. Балансовые модели. Модель Леонтьева.

10. Элементы теории матричных игр

11. Литература

1. Основные понятия исследования операций

Под исследованием операций понимается комплексная математическая дисциплина, занимающаяся построением, анализом и применением математических моделей принятия оптимальных решений.

Основной задачей исследования операций является задача выбора в заданном множестве элемента, удовлетворяющего заданным критериям оптимальности. При этом под критерием оптимальности понимается признак, на основании которого проводится сравнительная оценка возможных решений и затем выбирается оптимальное.

Каждое операционное исследование последовательно проходит следующие основные этапы:

1. Постановка задачи.

2. Построение математической модели.

3. Выбор метода решения задачи.

4. Проверка решения и корректировка модели.

5. Реализация найденного решения на практике.

В зависимости от условий внешней среды, состояния и степени информированности лица, принимающего решение, различают следующие задачи исследования операций.

Если принятие решения происходит в наперед известном и не изменяющемся во времени информационном состоянии лица, принимающего решения, то задачу называют статической.

Если в процессе принятия решения информационное состояние лица, принимающего решения, изменяется во времени, то задачу называют динамической.

Если все условия операции и состояния объекта исследования полностью известны заранее, то задачу называют детерминированной.

В случае, когда с каждой принимаемой стратегией связано множество возможных результатов и известны вероятности пребывания объекта исследований в каждом из состояний, задачу называют стохастической или задачей принятия решений в условиях риска.

Если информация о вероятностях пребывания объекта в том или ином состоянии отсутствует, то задачу называют задачей принятия решений в условиях неопределенности.

Решение задач исследования операций существенно зависит от выбора показателя эффективности. Критерием оптимальности может быть требование о максимизации или минимизации некоторой скалярной функции определенной на множестве допустимых решений и называемой целевой функцией. В этом случае задачу исследования операций называют задачей математического программирования. Если же критерием оптимальности является требование о максимизации или минимизации нескольких скалярных функций, то говорят о задаче многокритериальной оптимизации.

2. Геометрическая интерпретация задач оптимизации

Рассмотрим задачу оптимизации, заключающуюся в отыскании точек минимума или максимума функции, заданной на некотором множестве.

Общая задача теории оптимизации может быть сформулирована следующим образом.

Дана система неравенств и уравнений с n переменными.

(2.1)

и функция .

В области решений системы ограничений (2.1) требуется найти такое решение, при котором целевая функция z принимает наибольшее или наименьшее значение.

Для геометрической интерпретации задач оптимизации рассмотрим двухмерный случай. Изобразим на плоскости множество X решений системы (2.1) и несколько линий уровня целевой функции , k = 1,2,3…

Рис. 2.1

Задача оптимизации сводится к нахождению максимального (минимального) z^* среди всех z_k, для которых линии уровня пересекаются с областью X. При этом любая точка , лежащая в X на линии уровня , является оптимальным решением задачи.

На геометрическом толковании основан соответствующий метод решения задач оптимизации. В качестве примера рассмотрим линейную задачу:

→ min(max) (2.2)

(2.3)

Область решений системы (2.3) представляет собой гипермногогранник (полиэдр) в n – мерном пространстве, а целевая функция задает в этом пространстве гиперплоскость. Если n=2, то решение системы (2.3) есть плоский многогранник, а целевая функция при каждом фиксированном значении z описывает прямую на плоскости. В случае n=3 решение системы (2.3) образует многогранник в пространстве. При этом целевая функция (2.2) при различных значениях z образует семейство параллельных плоскостей в трехмерном пространстве.

Применим графический метод для решения задачи.

С целью обеспечения высокого объема перевозок железная дорога имеет возможность рекламировать свою деятельность, используя местные радио и телевизионные сети. Затраты на рекламу ограничены величиной 3000 условных денежных единиц. Каждая минута радиорекламы обходится в 20 условных денежных единиц, а минута телерекламы – в 60 единиц. Исходя из своих конъюнктурных соображений, железная дорога хотела бы использовать радиосеть по крайней мере в 2 раза чаще, чем телесеть. Радиокомпания согласна предоставить рекламное время в объеме не более 100 минут. Одна минута телерекламы обеспечивает объем перевозок в 6 раз превышающий объем перевозок, обеспечиваемый радиорекламой. Найти оптимальное распределение финансовых средств между телевизионной и радиорекламой.

Обозначим за х₁ и х₂ количество времени, затрачиваемого на радио и телерекламу, соответственно. Если W – объем перевозок, обеспечиваемый 1 мин. радиорекламы, а z – общий объем перевозок, то целевая функция может быть записана в виде

.

Так как величина W считается постоянной, вместо функции можно рассматривать функцию

,

максимум которой в некоторой области достигается в тех же точках, что и функцией .

Из условия задачи можно записать ограничения в виде неравенств, связанные с ограниченностью средств на рекламу

,

а так же с конъюнктурными интересами железной дороги

.

Кроме того, имеются ограничения, связанные с объемом времени на рекламу

; ; .

Таким образом, рассматриваемая задача записывается в виде

(2.4)

(2.5)

Каждое из неравенств описывает полуплоскость, и областью решений системы будет многоугольник, являющийся пересечением всех пяти полуплоскостей. Границы полуплоскостей описываются равенствами.

20х₁+60х₂=3000

х₁-2х₂=0

х₁=100 (2.6)

х₁=0

х₂=0

x₁

y=60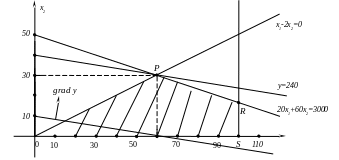

Рис. 2.2.

Решение системы неравенств (2.5) образует на плоскости четырехугольник OPRS, а целевая функция при различных значениях у образует на плоскости параллельные прямые (рис. 2.2). При этом значение у возрастет в направлении вектора

Отыскав направление возрастания функции у, будем перемещать вдоль этого вектора прямую, соответствующую целевой функции у, до тех пор, пока она не выйдет за пределы области OPRS. Это происходит в точке P, в которой и достигается максимальное значение функции у (а вместе с ней и z) в области OPRS.

Уточним координаты точки Р. Для этого учтем, что она является точкой пересечения прямых, описываемых уравнениями

Решив систему, найдем координаты точки Р (60;30). Это означает, что для получения наибольшего объема перевозок необходимо выделить средства на 60 мин. радиорекламы в размере 1200 условных единиц и на 30 мин. телерекламы в размере 1800 условных единиц.

Замечание. Иногда задача имеет не одно оптимальное решение. Это возможно, когда прямая, изображающая целевую функцию, параллельна одной из границ области допустимых значений.