
Виды экстремумов.
Локальный экстремум - это точка, в которой достигается наибольшее (или наименьшее) значение функции в НЕКОТОРОЙ (сколь угодно малой) ОКРЕСТНОСТИ данной точки.
Условный экстремум - это точка, в которой достигается наибольшее (или наименьшее) значение функции, при некотором УСЛОВИИ на переменную.
(условный экстремум, так же, как и обычный, может быть локальным и глобальным).
Локальный условный экстремум - это точка, в которой достигается наибольшее (или наименьшее) значение функции в НЕКОТОРОЙ (сколь угодно малой) ОКРЕСТНОСТИ данной точки, НА МНОЖЕСТВЕ, удовлетворяющем условию связи.
Глобальный условный экстремум - это точка, в которой достигается наибольшее (или наименьшее) значение функции НА ВСЁМ МНОЖЕСТВЕ, удовлетворяющем условию связи.
Экстремум в Математическом анализе.
a) Монотонность функции:
Функция
 называется возрастающей на промежутке
называется возрастающей на промежутке
 ,
если
,
если
 для любых точек
для любых точек
 и
и
 из промежутка
,
удовлетворяющих неравенству
из промежутка
,
удовлетворяющих неравенству
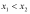 .
Функция называется убывающей на
,
если из условия
следует
.
Функция называется убывающей на
,
если из условия
следует
 .
.
Теорема.
Если функция
 непрерывна на отрезке
непрерывна на отрезке
 ,
дифференцируема на интервале
,
дифференцируема на интервале
 ,
то для того, чтобы
,
то для того, чтобы
 была возрастающей (убывающей) необходимо
и достаточно, чтобы
была возрастающей (убывающей) необходимо
и достаточно, чтобы

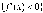 в каждой внутренней точке интервала
.
в каждой внутренней точке интервала
.
Дифференцируемая
функция является возрастающей на
промежутке
тогда и только тогда, когда
 .
.
Пример.
Найти промежутки возрастания и убывания
функции
 .
.
Вычислим:
 :
:
 .
.
Точки
 делят числовую прямую
делят числовую прямую
 на три интервала:
на три интервала:
 .
.
Производная
положительна на интервалах
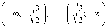 .
Следовательно, функция
.
Следовательно, функция
 возрастает на каждом из этих интервалов.
На интервале
возрастает на каждом из этих интервалов.
На интервале
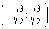 производная
неположительная, значит,
убывает на этом интервале.
производная
неположительная, значит,
убывает на этом интервале.
б) Локальный экстремум:
Точка
 называется точкой локального максимума
функции
называется точкой локального максимума
функции
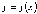 ,
если существует интервал
,
если существует интервал
 ,
содержащий точку
такой что
,
содержащий точку
такой что
 .
.
Точка
называется точкой локального минимума
функции
,
если существует интервал
,
содержащий точку
такой что
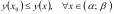 .
.
Точки локального минимума и локального максимума называются точками локального экстремума.
Необходимым
условием локального экстремума
дифференцируемой функции является
выполнение равенства
 .
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
.
Поэтому точки, в которых дифференцируемая
функция может иметь локальный экстремум,
находят, решая уравнение:
Решения этого уравнения называют стационарными точками.
в) Исследование стационарных точек:
I
правило.
Если при возрастании
 при переходе через стационарную точку
производная
меняет знак с + на , то
точка локального максимума. Если
меняет знак с на + , то
при переходе через стационарную точку
производная
меняет знак с + на , то
точка локального максимума. Если
меняет знак с на + , то
 точка локального минимума функции
точка локального минимума функции
 .
Если
.
Если
 не меняет знак в точке
,
то экстремума нет.
не меняет знак в точке
,
то экстремума нет.
II
правило.
Если вторая производная
 в стационарной точке
положительная, то
точка локального минимума функции
.
Если вторая производная
в стационарной точке
отрицательная, то
точка локального максимума функции
.
в стационарной точке
положительная, то
точка локального минимума функции
.
Если вторая производная
в стационарной точке
отрицательная, то
точка локального максимума функции
.
Точками локального экстремума функции могут быть такие точки, в которых производная не существует или обращается в бесконечность. Исследовать такие точки можно по I правилу. Экстремум в такой точке называется острым экстремумом.
Пример. Найти экстремум функции
 .
.
 .
.
Функция
имеет стационарную точку
 (в этой точке производная равна нулю).
В точке
(в этой точке производная равна нулю).
В точке
 производная обращается в бесконечность.
производная обращается в бесконечность.
Поскольку
 при
при
 и
и
 при
при
 ,
то функция имеет в точке
,
то функция имеет в точке
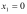 локальный минимум
локальный минимум
 .
Это будет острый минимум.
.
Это будет острый минимум.
При
переходе через стационарную точку

 производная меняет знак с на +, значит,
функция имеет локальный максимум.
производная меняет знак с на +, значит,
функция имеет локальный максимум.
г) Глобальный экстремум
Непрерывная
на отрезке
 функция
функция
 принимает свое наибольшее значение
принимает свое наибольшее значение
 и свое наименьшее значение
и свое наименьшее значение
 в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
и
поступают следующим образом.
в точках этого отрезка. Эти значения
могут достигаться либо в стационарных
точках отрезка, либо в точках
недифференцируемости функции, либо в
граничных точках отрезка. Поэтому для
нахождения значений
и
поступают следующим образом.
Находят стационарные точки
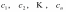 функции;
функции;Находят точки
 ,
в которых производная
,
в которых производная
 не существует или обращается в
бесконечность;
не существует или обращается в
бесконечность;Вычисляют значения:
 и
выбирают среди этих чисел наибольшее
и наименьшее.
и
выбирают среди этих чисел наибольшее
и наименьшее.
Это
и будут
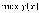 и
и
 глобальные экстремальные значения.
глобальные экстремальные значения.
Пример.
Найти наибольшее и наименьшее значения
функции
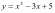 на отрезке
на отрезке
 .
.
 ;
;
 .
.
Вычисляем
 .
Получаем числа
.
Получаем числа
 .
Следовательно,
.
Следовательно,
 ,
,
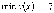 .
.
Исследование функции и построение графика.
График
функции
 ,
заданной на множестве
,
заданной на множестве
 ,
т.е. множество точек плоскости с
координатами
,
т.е. множество точек плоскости с
координатами
 ,
обычно строят с некоторой степенью
приближения, так как точное построение
невозможно.
,
обычно строят с некоторой степенью
приближения, так как точное построение
невозможно.
Для
построения графика функции
 выясняют особенности поведения функции.
Существенную роль при этом играют
характерные точки: концевые точки
промежутков задания функции, точки
разрыва, стационарные точки и точки
недифференцируемости функции и ее
производной и т.д. По этим точкам
выделяются участки однообразного
поведения функции, а именно: промежутки
ее непрерывности; промежутки, на которых
выясняют особенности поведения функции.
Существенную роль при этом играют
характерные точки: концевые точки
промежутков задания функции, точки
разрыва, стационарные точки и точки
недифференцируемости функции и ее
производной и т.д. По этим точкам
выделяются участки однообразного
поведения функции, а именно: промежутки
ее непрерывности; промежутки, на которых
 и
и
 сохраняют знак, что позволяет изучить
характер монотонности функции и
направление ее выпуклости.
сохраняют знак, что позволяет изучить
характер монотонности функции и
направление ее выпуклости.
Построение графика функции может быть осуществлено по следующему плану:
Если
функция задана аналитическими выражениями,
то выясняют естественную область
определения функции, т.е. множество
значений аргумента
 ,
при которых
,
при которых
 имеет смысл.
имеет смысл.
Если
функция периодическая, то находят ее
период, т.е. число
 такое, что
такое, что
 ,
,
 (обычно рассматривают наименьший
положительный период). Дальнейшее
изучение функции и построение графика
проводят для какого-либо отрезка длины
,
например, для
(обычно рассматривают наименьший
положительный период). Дальнейшее
изучение функции и построение графика
проводят для какого-либо отрезка длины
,
например, для
 ,
а затем периодически продолжают.
,
а затем периодически продолжают.
Для
четной функции:
 ,
или нечетной:
,
или нечетной:
 .
Исследование проводят на промежутке
.
Исследование проводят на промежутке
 .
Построенный график продолжают на все
множество
.
Построенный график продолжают на все
множество
 ,
используя симметричное отражение
относительно оси
,
используя симметричное отражение
относительно оси
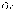 для четной функции и относительно точки
для четной функции и относительно точки
 для нечетной функции.
для нечетной функции.
Находят
точки разрыва и промежутки, на которых
она непрерывна. Выясняют характер точек
разрыва. Вычисляют предельные значения
функции в граничных точках множества
(если таковые имеются). Находят вертикальные
асимптоты (в точках бесконечного скачка).
Если
не ограничено, то вычисляют пределы
функции при
 и
и
 .
Если
.
Если
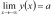 ,
то график имеет горизонтальную
левостороннюю асимптоту
,
то график имеет горизонтальную
левостороннюю асимптоту
 ,
если
,
если
 ,
график имеет горизонтальную правостороннюю
асимптоту
,
график имеет горизонтальную правостороннюю
асимптоту
 .
Если пределы (или один из пределов)
бесконечны, то график может иметь
наклонные (левостороннюю и правостороннюю)
асимптоты
.
Если пределы (или один из пределов)
бесконечны, то график может иметь
наклонные (левостороннюю и правостороннюю)
асимптоты
 .
Коэффициенты левосторонней асимптоты
можно найти по формулам:
.
Коэффициенты левосторонней асимптоты
можно найти по формулам:

Аналогично
находят коэффициенты правосторонней
асимптоты (нужно вычислить пределы при
 ).
).
Вычисляют
производную
 .
Находят критические точки функции
.
Находят критические точки функции
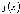 ,
т.е. стационарные точки и точки, в которых
,
т.е. стационарные точки и точки, в которых
 не существует. Выделяют промежутки, на
которых
сохраняет знак. Это позволяет исследовать
монотонность функции
.
не существует. Выделяют промежутки, на
которых
сохраняет знак. Это позволяет исследовать
монотонность функции
.
Вычисляют
вторую производную
 .
Находят критические точки производной
.
Выделяют промежутки, на которых
сохраняет знак, и, следовательно, график
функции
сохраняет направление выпуклости.
Находят точки перегиба, исследуя
критические точки производной
(т.е. точки, в которых
равны нулю или не существуют).
.
Находят критические точки производной
.
Выделяют промежутки, на которых
сохраняет знак, и, следовательно, график
функции
сохраняет направление выпуклости.
Находят точки перегиба, исследуя
критические точки производной
(т.е. точки, в которых
равны нулю или не существуют).
Исследуя стационарные точки функции , находят точки локального экстремума и локальные экстремальные значения функции. Для этого можно изучить поведение производной в окрестности стационарной точки или значение в стационарной точке. Изучают точки недифференцируемости функции, выясняя наличие локальных экстремумов в таких точках по поведению производной в их окрестностях.
Опираясь на характерные точки функции, строят таблицу, в которую вносят все особенности функции.
На координатную плоскость в выбранном масштабе наносят характерные точки функции, асимптоты и строят график, руководствуясь п. 16. Если нужно, строят дополнительно несколько точек графика.
