Приклади виконання завдання
Задача 1. Важке
тіло масою m рухається вниз по жорсткій
площині, нахиленої під кутом
до горизонту. Початкова швидкість тіла
дорівнює
.
Коефіцієнт тертя
Визначити рівняння руху і шлях, який пройшло тіло за час t=2с.
Розв’язання. Приймаючи тіло за матеріальну точку, розглянемо його рух під дією сил, прикладених до нього.
Щоб правильно
вказати схему сил, розглянемо з якими
тілами взаємодіє тіло. Воно взаємодіє
з похилою площиною і повітрям, опором
якого нехтуємо. Сила взаємодії тіла з
Землею є сила ваги G=mg.
Реакція площини має дві складові:
нормальну складову
та силу тертя
(рис. 3.2).
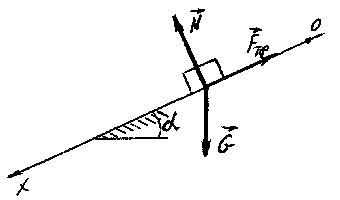
Рис. 3.2
Напрямимо вісь ОХ
паралельно траєкторії в бік руху тіла
і складемо диференціальне рівняння
руху матеріальної точки в проекції на
вісь ОХ:
,
тобто
.
Але за законом
сухого тертя
,
тобто
,
або
.
(a)
Звідки інтегруванням знайдемо Х як функцію часу t.
Враховуючи, що
(а) запишимо у вигляді:
.
В результаті першого інтегрування невизначеним інтегралом матимемо:
.
Сталу інтегрування
знайдемо з початкових умов: при t=0
=2м/с.
Дістанемо
.
Отже,
.
Інтегруючи вдруге,
з врахуванням що
,
тобто
,
матимемо
:
.
(б)
Сталу інтегрування
знайдемо з початкових умов: при t=0 x=0
(початок координат знаходиться в
початковому положенні точки). Дістанемо
.
Після підстановки в (б)
маємо рівняння
,
(в)
яке є законом руху точки.
Для визначення
шуканого шляху s за
секунд, покладемо у рівнянні руху точки
(в) t=
,
і
дістанемо
.
При
матимемо
.
Відповідь:
рівняння
руху
;
шлях
.
Таблиця - Вихідні дані до задачі Д.2
№ варіанта |
, град. |
V0, м/с |
|
t1, c. |
S, м |
00 |
60 |
2 |
0,40 |
3 |
? |
01 |
45 |
4 |
0,30 |
? |
5 |
02 |
30 |
6 |
0,20 |
2 |
? |
03 |
30 |
8 |
0,10 |
5 |
? |
04 |
45 |
10 |
0,15 |
? |
4 |
05 |
60 |
12 |
0,20 |
? |
6 |
06 |
60 |
16 |
0,25 |
1 |
? |
07 |
45 |
18 |
0,30 |
6 |
? |
08 |
30 |
20 |
0,35 |
? |
10 |
09 |
30 |
20 |
0,40 |
? |
8 |
10 |
60 |
18 |
0,35 |
2 |
? |
11 |
45 |
16 |
0,30 |
4 |
? |
12 |
45 |
14 |
0,25 |
5 |
? |
13 |
60 |
12 |
0,20 |
6 |
? |
14 |
30 |
10 |
0,15 |
? |
4 |
15 |
45 |
8 |
0,10 |
? |
8 |
16 |
30 |
6 |
0,10 |
? |
10 |
17 |
60 |
4 |
0,15 |
2 |
? |
18 |
45 |
2 |
0,20 |
3 |
? |
19 |
45 |
3 |
0,25 |
? |
5 |
20 |
60 |
4 |
0,30 |
5 |
? |
21 |
30 |
5 |
0,35 |
6 |
? |
22 |
30 |
6 |
0,40 |
? |
6 |
23 |
45 |
7 |
0,45 |
10 |
? |
24 |
60 |
8 |
0,35 |
? |
8 |
25 |
60 |
9 |
0,30 |
? |
10 |
26 |
30 |
10 |
0,25 |
6 |
? |
27 |
45 |
10 |
0,20 |
3 |
? |
28 |
30 |
15 |
0,15 |
? |
3 |
29 |
45 |
25 |
0,25 |
2 |
? |
30 |
60 |
30 |
0,35 |
? |
2 |