Запитання для самоконтролю

1. Що називається диференціальним рівнянням n-го порядку ? Як визначити порядок диференціального рівняння ?

2. У чому полягає задача Коші для диференціального рівняння n-го порядку?

3. Сформулюйте задачу Коші і теорему про існування розв’язку рівняння ).

4. Що називається загальним розв’язком рівняння n-го порядку ? Як знайти його окремий розв’язок ?

5. У чому суть методу пониження порядку диференціального рівняння ?

6. Що називається лінійним диференціальним рівнянням n-го порядку?

7. Що називається лінійним однорідним диференціальним рівнянням другого порядку ?

8. Як знайти загальний розв’язок лінійного однорідного рівняння другого порядку , якщо відомо його частинний розв’язок .

Системи диференціальних рівнянь

У багатьох науково-технічних задачах буває потрібно знайти не одну, а зразу кілька невідомих функцій , які пов’язані між собою кількома диференціальними рівняннями . Сукупність таких рівнянь утворює систему диференціальних рівнянь.

§14.Нормальні системи рівнянь .

Нормальною системою диференціальних рівнянь називається система виду

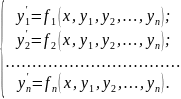(1)

Розв’язком системи (1) називається сукупність функцій 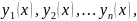які задовольняють кожному з рівнянь цієї системи.

Початковими умовами для системи (1) називають умови вигляду

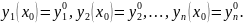(2)

Задача знаходження розв’язку системи диференціальних рівнянь , який задовольняє умови ( 2) , називається задачею Коші для системи (2).

Нормальну систему рівнянь можна замінити одним рівнянням , порядок якого дорівнює числу рівнянь системи . Продиференціюємо по перше рівняння : 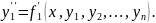Підставивши в цю рівність значення похідних 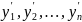з системи (1), дістанемо 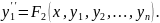Аналогічно знаходимо похідні до n- го порядку включно .

Дістаємо систему рівнянь

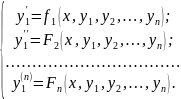
Якщо з перших n-1 рівнянь системи (1) знайти ( коли це можливо ) змінні 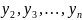і підставивши їх значення в останнє рівняння , то одержимо рівняння n- го порядку відносно змінної

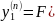
Приклад. Розв’язати систему рівнянь

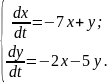
∆ Продиференціюємо перше рівняння :

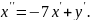
Підставимо в це рівняння значення похідної із другого рівняння системи :

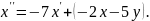
Знайшовши з першого рівняння значення 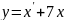і підставивши його в знайдене рівняння , дістанемо

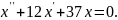
Маємо лінійне однорідне рівняння другого порядку із сталими коефіцієнтами. Інтегруючи його , одержуємо

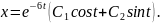
Оскільки , то

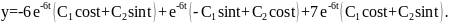
Отже , загальний розв’язок даної системи має вигляд

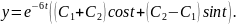
Вправи:

Розв’язати системи рівнянь :

128. 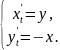129.

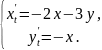
130. 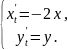131.

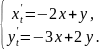
132. 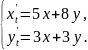133.

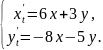
134. 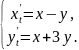135.

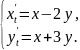
136. 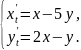137.

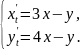
138. 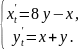139.

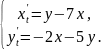
Методом виключення розв’язати систему диференціальних рівнянь :

140. 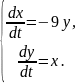141.

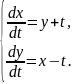
142.

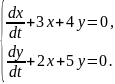
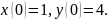
143.

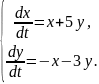
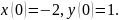
144. 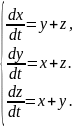145.