- •§1.Поняття про диференціальні рівняння
- •§2. Приклади задач , що приводять до диференціальних рівнянь .
- •§ 3. Диференціальні рівняння першого порядку з відокремленими змінними .
- •§4. Диференціальні рівняння першого порядку з відокремлюваними змінними .
- •§5. Однорідні диференціальні рівняння першого порядку
- •§6. Лінійні диференціальні рівняння першого порядку .
- •Алгоритм розв’язання
- •§7.Рівняння , які зводяться до лінійних . Рівняння Бернуллі та Ріккаті .
- •8. Рівняння в повних диференціалах .
- •Деякі застосування диференціальних рівнянь першого порядку .
- •Запитання для самоконтролю:
- •Диференціальні рівняння вищих порядків.
- •§10.Основні поняття та означення . Задача Коші.
- •§11.Простіші диференціальні рівняння другого порядку .
- •§12. Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами .
- •§13. Лінійні неоднорідні рівняння другого порядку.
- •Запитання для самоконтролю
- •Системи диференціальних рівнянь
- •§14.Нормальні системи рівнянь .
- •Список літератури
Алгоритм розв’язання
Зводимо рівняння до виду
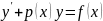 .
.Використовуючи підстановку знаходять і підставляють ці вирази в рівняння .
Групують члени рівняння , виносять одну із функцій
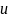 або
або
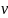 за дужки. Знаходять другу функцію ,
прирівнявши вираз в дужках до нуля і
розв’язавши одержане рівняння .
за дужки. Знаходять другу функцію ,
прирівнявши вираз в дужках до нуля і
розв’язавши одержане рівняння .Підставляють знайдену функцію в вираз , що залишився і знаходять другу функцію .
Записують загальний розв’язок , підставивши вираз для знайдених функцій і в рівність
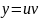 .
.Якщо потрібно знайти частинний розв’язок , то визначають С із початкових умов і підставляють в загальний розв’язок .
Приклад.
Знайти
загальний розв’язок рівняння
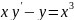 .
.
Запишемо
дане рівняння у вигляді
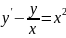 .
.
Використовуємо
підстановку
, звідки
.
Підставляємо значення
і
в останнє рівняння :
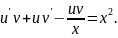
Згрупуємо члени , що містять , і винесемо за дужки :
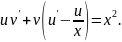
Знайдемо
функцію
таку , що
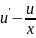 =0. Розв’язуємо це рівняння як рівняння
з відокремлюваними змінними , тобто
=0. Розв’язуємо це рівняння як рівняння
з відокремлюваними змінними , тобто
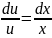 , звідси після інтегрування , одержимо
, звідси після інтегрування , одержимо
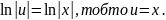
Підставивши
значення функції
в рівняння, знайдемо
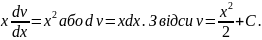
Отже, загальним розв’язком даного рівняння є функція
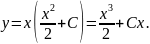
Вправи:
Знайти загальні розв’язки лінійних рівнянь :
51.
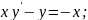 52.
52.
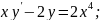
53.
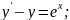 54.
54.
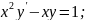
55.
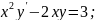 56.
56.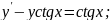
57.
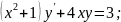 58.
58.
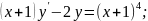
59.
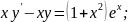 60.
60.
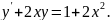
Знайти частинні розв’язки рівнянь :
61.
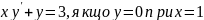 .
.
62.
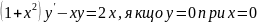 .
.
63.
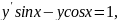
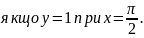
64.
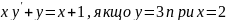 .
.
65.
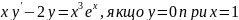 .
.
§7.Рівняння , які зводяться до лінійних . Рівняння Бернуллі та Ріккаті .
Розглянемо класи рівнянь , які за допомогою певних перетворень можна звести до лінійних .
Рівнянням
Бернуллі
називається рівняння виду
 .
.
При
n=0
це рівняння - лінійне , а при n=1
– з відокремлюваними змінними. Припускаючи
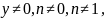 поділимо
дане рівняння на
поділимо
дане рівняння на
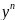 ,
тоді матимемо рівняння виду
,
тоді матимемо рівняння виду

Таким
чином , заміною
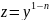 рівняння Бернуллі зводиться до лінійного
рівняння . Проте на практиці розв’язок
рівняння Бернуллі зручніше шукати
методом Бернуллі у вигляді
, не зводячи його до лінійного . Слід
зазначити , що при
рівняння Бернуллі зводиться до лінійного
рівняння . Проте на практиці розв’язок
рівняння Бернуллі зручніше шукати
методом Бернуллі у вигляді
, не зводячи його до лінійного . Слід
зазначити , що при
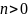 , крім розв’язку
, крім розв’язку
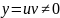 ,
рівняння Бернуллі має розв’язок
,
рівняння Бернуллі має розв’язок

Рівнянням Ріккаті називається рівняння виду
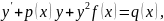
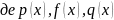 - задані
функції .
- задані
функції .
Якщо
p , f , q – сталі числа , то це рівняння
інтегрується відокремленням змінних
. Коли
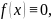 то дане рівняння стає лінійним , а у
випадку
то дане рівняння стає лінійним , а у
випадку
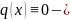 рівнянням
Бернуллі . У загальному випадку рівняння
Ріккаті
не інтегрується в квадратурах . Проте
якщо відомо його один частинний розв’язок
рівнянням
Бернуллі . У загальному випадку рівняння
Ріккаті
не інтегрується в квадратурах . Проте
якщо відомо його один частинний розв’язок
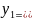
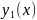 ,
то заміною
,
то заміною
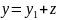 рівняння Ріккаті
зводиться до рівняння Бернуллі .
рівняння Ріккаті
зводиться до рівняння Бернуллі .
Приклад.
Розв’язати
рівняння
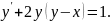
Задане рівняння
є рівнянням
Ріккаті
. Неважко
пересвідчитись , що функція у
= х
- розв’язок цього рівняння , тому заміна
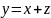 зводить
його до
рівняння Бернуллі :
зводить
його до
рівняння Бернуллі :
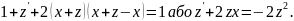
Далі
маємо
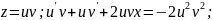
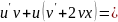 -
-
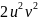 ;
;
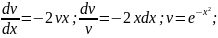
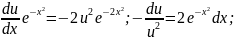
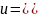
Отже , розв’язком даного рівняння є :
у
= х
;
=
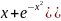
Вправи
Розв’язати рівняння Бернуллі :
66.
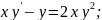 67.
67.
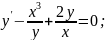
68.
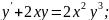 69.
69.
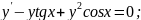
70.
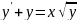 ; 71.
; 71.
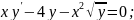
72.
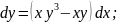 73.
73.