
- •§1.Поняття про диференціальні рівняння
- •§2. Приклади задач , що приводять до диференціальних рівнянь .
- •§ 3. Диференціальні рівняння першого порядку з відокремленими змінними .
- •§4. Диференціальні рівняння першого порядку з відокремлюваними змінними .
- •§5. Однорідні диференціальні рівняння першого порядку
- •§6. Лінійні диференціальні рівняння першого порядку .
- •Алгоритм розв’язання
- •§7.Рівняння , які зводяться до лінійних . Рівняння Бернуллі та Ріккаті .
- •8. Рівняння в повних диференціалах .
- •Деякі застосування диференціальних рівнянь першого порядку .
- •Запитання для самоконтролю:
- •Диференціальні рівняння вищих порядків.
- •§10.Основні поняття та означення . Задача Коші.
- •§11.Простіші диференціальні рівняння другого порядку .
- •§12. Лінійні однорідні рівняння другого порядку із сталими коефіцієнтами .
- •§13. Лінійні неоднорідні рівняння другого порядку.
- •Запитання для самоконтролю
- •Системи диференціальних рівнянь
- •§14.Нормальні системи рівнянь .
- •Список літератури
§ 3. Диференціальні рівняння першого порядку з відокремленими змінними .
Рівняння
виду
 - дані функції , називається рівнянням
з
відокремленими
змінними
.
- дані функції , називається рівнянням
з
відокремленими
змінними
.
Це
рівняння можна переписати у вигляді
 .
.
Розв’язуються такі рівняння безпосереднім інтегруванням .
Приклад.
Розв’язати рівняння

Розв’язання . Змінні тут розділені . Інтегруючи , одержимо

Знайти загальні розв’язки рівнянь :
15.
 )
) ; 16.
; 16.
 ;
;
17.
 18.
18.
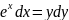 ;
;
19.
 ; 20.
; 20.
 ;
;
Знайти частинні розв’язки рівнянь :
21.
 ;
;
22.

23.

§4. Диференціальні рівняння першого порядку з відокремлюваними змінними .
Рівняння
вигляду

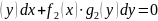 , де
, де
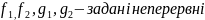 функції
, називається рівнянням з відокремлюваними
змінними
.
функції
, називається рівнянням з відокремлюваними
змінними
.
Спосіб
інтегрування .
Відокремити змінні , поділивши обидві
частини рівняння на
 ,
і проінтегрувати :
,
і проінтегрувати :

Приклад
1. Розв’язати
рівняння :

Розв’язання.
Маємо диференціальне рівняння першого
порядку з відокремлюваними змінними .
Відокремимо змінні , поділивши праву і
ліву частину рівняння на
 Маємо
Маємо
 ,
,
 .
.
Інтегруючи ліву і праву частини останньої рівності , одержуємо
 =
-
=
- або
або
 , звідки
, звідки
 .
.
Вправи
Розв’язати рівняння :
24.
 25.
25.
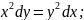
26.
 27.
27.

28.
 29.
29.

30.
 )
) 31.
31.


32.
 ;
;
33.

34.

Знайти частинні розв’язки рівнянь :
35 .

36.
 при
при

37.

38.

39.
 при
при
 ;
;
40 .
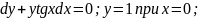
§5. Однорідні диференціальні рівняння першого порядку
Функція
 називається однорідною
функцією порядку
k
відносно
змінних x
і y
, якщо
називається однорідною
функцією порядку
k
відносно
змінних x
і y
, якщо

Наприклад
,
 – однорідна функція
третього порядку , оскільки
– однорідна функція
третього порядку , оскільки

Диференціальне
рівняння
першого порядку
 називається однорідним
якщо
функція
- однорідна функція нульового порядку.
називається однорідним
якщо
функція
- однорідна функція нульового порядку.
Його
можна записати у вигляді
 , де
, де
 - однорідні функції одного і того самого
порядку .
- однорідні функції одного і того самого
порядку .
Однорідні
диференціальні рівняння зводяться до
диференціальних рівнянь з відокремлюваними
змінними підстановкою
 - нова невідома функція .
- нова невідома функція .
Приклад
1. Знайти
розв’язок рівняння


В даному
рівнянні функції
 - однорідні другого порядку , тому дане
рівняння є однорідним. Замінимо
- однорідні другого порядку , тому дане
рівняння є однорідним. Замінимо
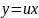 ,
звідси
,
звідси
 Підставляючи
ці вирази
Підставляючи
ці вирази
 і
і
 в дане рівняння
в дане рівняння

тобто
 або
або


Відокремлюємо
змінні ( вважаючи
 ):
):

Інтегруючи
почленно це рівняння ( враховуючи , що
 ):
):
 =
=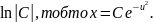
Повертаючись
до попередньої функції
 знаходимо
загальний інтеграл
знаходимо
загальний інтеграл

Вправи:
Розв’язати рівняння :
41 .
 ;
;
42.

43.
 ;
;
44.
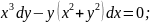
45.

46.

47.

Знайти частинні розв’язки рівнянь :
48.

49.


50.


§6. Лінійні диференціальні рівняння першого порядку .
Рівняння
вигляду
 яке лінійне відносно невідомої функції
та її похідної , називається лінійним
диференціальним рівнянням першого
порядку .
яке лінійне відносно невідомої функції
та її похідної , називається лінійним
диференціальним рівнянням першого
порядку .
Вважатимемо
, що p
i
f
–
задані функції , що визначені і неперервні
на

Якщо
 , то рівняння називається лінійним
однорідним ,
у протилежному випадку – лінійним
неоднорідним .
, то рівняння називається лінійним
однорідним ,
у протилежному випадку – лінійним
неоднорідним .
Лінійне однорідне рівняння є рівнянням з відокремлюваними змінними .
Є
кілька методів інтегрування лінійного
неоднорідного рівняння . Один із них (
метод Бернуллі ) полягає в тому , що
розв’язок цього рівняння рівняння
шукають у вигляді
 де
де
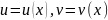 - невідомі функції
- невідомі функції
 ,
причому одна із них довільна ( але не
рівна тотожно нулю).
,
причому одна із них довільна ( але не
рівна тотожно нулю).
Знаходячи похідну
 і підставляючи значення
та
і підставляючи значення
та
 в рівняння , дістанемо
в рівняння , дістанемо

Користуючись
довільністю у виборі функції
 , доберемо її так , щоб
, доберемо її так , щоб
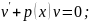 тоді
тоді
 Розв’яжемо
ці рівняння .
Розв’яжемо
ці рівняння .
