Нехай вектор а має початок у точці м1(х1, y1, z1), а кінець — у точці м2(х2, y2, z2). Тоді величини

є проекціями вектора a на осі х, y, z. Проекції вектора однозначно визначають вектор. Тому виконується рівність

Очевидно, що проекція на вісь х суми a + b векторів a та b дорівнює сумі проекцій на вісь х векторів a, b (рис. 6).

Рис. 6

● Справді, виконуються рівності

Нехай відомі проекції векторів a та b:

.

Тоді проекція суми векторів a + b дорівнює сумі відповідних проекцій векторів-доданків:

Означення. Добутком вектора a на число  називається вектор , довжина якого дорівнює . Вектор колінеарний вектору а; має однаковий з ним напрям при і протилежний напрям при . Якщо або , то маємо , тобто добуток є нуль-вектором.

Множення вектора на число має властивість асоціативності та дистрибутивності. Для довільних чисел ,  та векторів a, b справджуються рівності:

(1)

Останню рівність унаочнює рис. 7 ( ).

Рис. 7

Ця властивість випливає з подібності трикутників із коефіцієнтом подібності .

З очевидної рівності

випливає:

Лема. Будь-який вектор a можна єдиним чином подати у вигляді суми трьох векторів, кожний із яких колінеарний одній з осей координат х, у, z.

 Справді, нехай М₁ — початок вектора a, М₂ — його кінець. Сумістимо точку М₁ із початком координат. Опустимо з точки М₂ перпендикуляр на координатну площину ху і позначимо здобуту проекцію М₃. Із точки М₃ опустимо перпендикуляр на вісь х. Відповідну проекцію позначимо М₄. Вектор М₃М₂ колінеарний осі z, вектор М₄М₃ — осі у, а вектор М₁М₄ — осі х.

Звідси, скориставшись одиничними векторами i, j, k, що, як відомо, колінеарні осям х, у, z, дістанемо:

.

Оскільки виконується рівність (рис. 8),

Рис. 8

то вектор a можна записати у вигляді:

(2)

Вектори називаються компонентами вектора a.

Отже, кожний вектор дорівнює сумі його компонентів за трьома осями координат.

Якщо вектори a та b подано за їх компонентами:

то для їх лінійної комбінації маємо

. (3)

Д ано два вектори:

.

Знайдемо за формулою (3) вектор

.

Скалярний добуток векторів

Означення. Скалярним добутком векторів a і b називається число , що дорівнює добутку довжини цих векторів на косинус кута між ними (рис. 9):

(1)

Рис. 9

Нехай — проекція вектора b на вісь, паралельну вектору a. Тоді маємо:

(2)

Останнє співвідношення означає, що скалярний добуток двох векторів дорівнює модулю одного з них, помноженому на проекцію другого вектора на напрям першого.

Якщо кут між векторами a та b гострий, то ; якщо тупий, то ; якщо прямий, то . Коли один із векторів a, b є нульовим, то його можна вважати ортогональним до будь-якого іншого вектора.

Наведемо аналітичні властивості скалярного добутку, що випливають із його означення.

Остання рівність є наслідком формули (2) і властивості проекцій суми векторів:

Отже, у разі скалярного множення суми векторів на вектор можна розкривати дужки. Нехай вектори а та b подано через їх проекції на координатні осі:

Запишемо таблицю скалярного множення для одиничних векторів i, j, k — ортів системи координат:

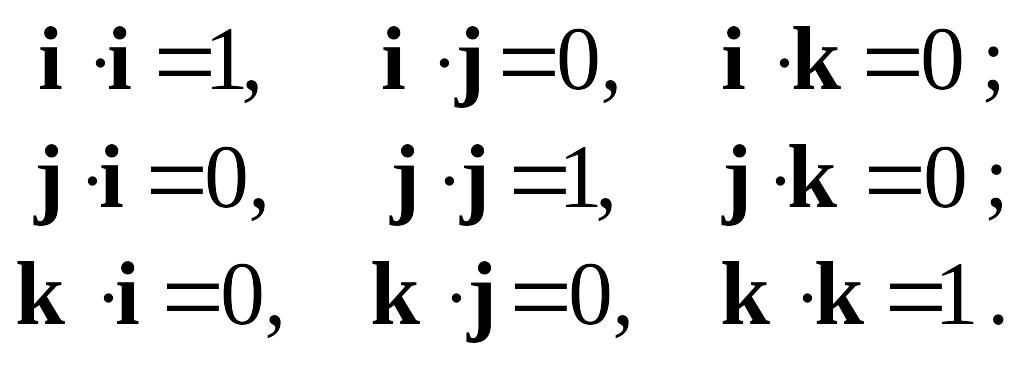
Перемноживши скалярно вектори a та b, знайдемо їх скалярний добуток у проекціях на координатні осі:

(3)

Звідси маємо:

Знаючи проекції векторів а, b, можна знайти кут між цими векторами:

Д ано просторовий трикутник з вершинами А(1, 2, –1), В(2, 4, 1), С(3, 0, 0). Знайдемо кут при вершині А.

 Розглянемо вектори

і з їх скалярного добутку визначимо косинус шуканого кута:

.

Оскільки скалярний добуток векторів a, b дорівнює нулю, то кут при вершині А прямий. 

Властивості додавання векторів та множення числа на вектор (  — деякі числа):

4. Для будь-якого вектора а існує протилежний вектор –а, такий що

Із означення скалярного добутку випливають такі його властивості:

З ауваження. Скалярному добутку можна дати економічну інтерпретацію, розглянувши m різних товарів відповідно кіль­кістю та ціною за одиницю товару. Загальну вартість усіх товарів можна подати скалярним добутком вектора кількості товарів і вектора цін :

Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001

гл.2, §1- 4, стор.32 – 57.

Тема 5

Різні види рівнянь прямої на площині

Мета заняття Вивчити різні види завдань прямої на площині та відповідні їм рівняння.

Розвивати просторове мислення.

Студенти повинні знати: означення напрямного та нормального векторів прямої; різні види рівнянь прямої на площині.

Студенти повинні вміти: знаходити різні види рівнянь прямої на площині відповідно способам завдання.

Основні питання теми

При вивченні цієї теми треба спочатку уважно прочитати матеріал, зробити конспект, в якому повинні бути зображені різні способи завдання проямої і записані відповідні їм рівняння. Це зручно зробити за наступним планом:

1.Поняття нормального та напрямного векторів прямої;

2.Пряма, що проходить через дану точку і має заданий напрямний вектор;

3.Пряма, що проходить через дві дані точки;

4.Пряма, що відрізає на осях координат задані відрізки;

5.Пряма, що проходить через дану точку і має заданий нормальний вектор;

6.Пряма що проходить через дану точку і має даний кутовий коефіциент;

Завдання для самоперевірки

Скласти рівняння прямої, що проходить:

1)через точки А(-4;3) і В(2;-1);

2)через точку М(5;3) паралельно прямій 2х – 4у = 7;

3)через точку Р(3;-4) під кутом° 30 до осі ОХ.

Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,

стор.76 – 80.

Лекція ”Пряма лінія на площині”

Нехай на площині задано пряму у прямокутній системі координат х, у. Кут  між віссю Ох і цією прямою називається кутом нахилу прямої до осі. Тангенс кута нахилу називається кутовим коефіцієнтом розглядуваної прямої. Якщо ця пряма перетинає вісь Оу у точці В з координатами (0, b), то число b називається початковою ординатою. Візьмемо довільну точку М(х, у) на прямій (рис. 1).

Рис. 1

З прямокутного трикутника МАВ знаходимо рівняння прямої

,

яке можна подати у вигляді

, де

(1)

Якщо розглядувана пряма паралельна осі Оу, то  = 0,5 і tg не існує. При цьому пряма має рівняння виду х = а (рис. 2).

Рис. 2

Координати х, у будь-якої точки М(х, у), що належить прямій, задовольняють рівняння (1). Якщо пряма (1) проходить через точку М₁(х₁, у₁), то справджується рівність

у₁ = kx₁ + b,

Віднімаючи почленно цю рівність від рівності (1), дістаємо рівняння прямої, що проходить через задану точку:

(2)

Зі зміною кутового коефіцієнта k в рівнянні (2) утворюються різні прямі, що проходять через точку М₁(х₁, у₁). Рівняння (2) називається рівнянням пучка (в’язки) прямих (рис. 3).

Рис. 3

Нехай дано дві різні точки М₁(х₁, у₁), М₂ (х₂, у₂), де х₂  х₁. З рівняння (2) випливає вираз для кутового коефіцієнта прямої, що проходить через точки М₁, М₂:

(3)

Підставляючи в (3) рівняння (2), знаходимо рівняння прямої, що проходить через дві задані точки М₁(х₁, у₁), М₂ (х₂, у₂):

(4)

З найдемо рівняння прямої, що проходить через дві точки М₁(4, 1), М₂(2, 3).

 Згідно з (4) маємо:

Ця пряма утворює кут 135 з віссю Ох. 

Якщо задано вектор , паралельний деякій прямій, і точку М₀(х₀, у₀) на цій прямій, то рівняння прямої можна записати у вигляді

Вектор s називається напрямним вектором прямої.

Щоб побудувати графік прямої, достатньо знати дві її різні точки і через них провести пряму. Якщо пряма перетинає осі координат у точках М₁(а, 0), М₂(0, b), а  0, b  0, то її можна записати рівнянням

(5)

яке називається рівнянням прямої у відрізках на осях.

З апишемо рівняння прямої

у вигляді (5).

 Значенню у₁ = 0 відповідає х₁ = 3. При х₂ = 0 знаходимо у₂ = 2. Отже, шукане рівняння прямої подається у вигляді

Пряма перетинає вісь х у точці з координатою х = 3, а вісь у — у точці з координатою у = 2. 

Розглянемо на площині прямокутну систему координат х, у і знайдемо рівняння прямої, коли відомий вектор її нормалі і задано точку М₀(х₀, у₀) на цій прямій. Нехай М(х, у) — довільна точка шуканої прямої (рис. 4).

Рис. 4

За умовою вектор перпендикулярний до вектора . Тому їх скалярний добуток . Звідси маємо рівняння

(1)

або

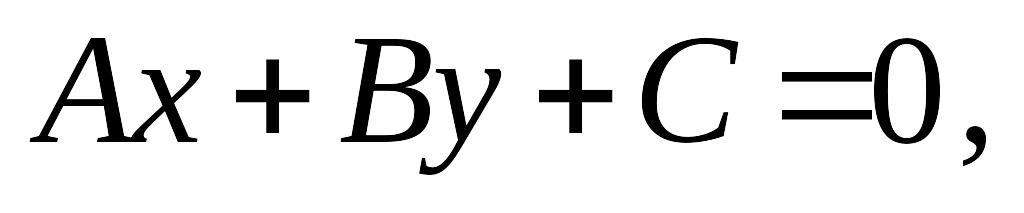
(2)

Це рівняння називається загальним рівнянням прямої.

На відміну від рівняння виду (1) змінні х, у входять до рівняння (2) рівноправно. Рівняння (1) завжди можна подати у вигляді (2).

Рівняння прямої (2) можна записати у вигляді (y = kx + b) лише за умови В  0.

Коефіцієнти А, В при х, у у загальному рівнянні прямої є про- екціями на координатні осі вектора її нормалі n.

Справджується теорема.

Теорема 1. Будь-яка пряма на площині може бути задана лінійним рівнянням виду (2). Кожне лінійне рівняння виду (2), де А² + В² > 0, визначає деяку пряму.

Доведення. Перше твердження теореми було доведено раніше при виведенні рівняння (1). Доведемо друге твердження. Візьмемо довільне лінійне рівняння

Оскільки коефіцієнти при х, у не перетворюються одночасно на нуль, завжди знайдуться значення х = х₀, у = у₀, при яких виконується рівність

Ах₀ + Ву₀ + С = 0.

Віднімаючи ці рівняння почленно, дістаємо рівність

А(х – х₀) + В(у – у₀) = 0. (3)

За допомогою векторів

,

рівність (3) можна записати у вигляді .

Як бачимо з рис. 3.27, вектор тоді і тільки тоді буде перпендикулярним до ненульового вектора , коли точка М(х, у) лежить на прямій, що проходить через точку М₀(х₀, у₀) перпендикулярно до цього вектора. Звідси випливає рівняння (1), що визначає деяку пряму. Отже, теорему доведено. 

Нехай х, у — координати довільної точки на площині. Пряма (2) поділяє всю площину на дві півплощини. В одній півплощині виконується нерівність Ах + Ву + С > 0, а в іншій — нерівність Ах + Ву + С < 0. На самій прямій маємо: Ах + Ву + С = 0.

Розглянемо частинні випадки рівняння (2):

якщо А = 0, то пряма паралельна осі х;

якщо В = 0, то пряма паралельна осі у;

якщо С = 0, то пряма проходить через початок координат;

якщо А = 0, С = 0, то пряма збігається з віссю х;

якщо В = 0, С = 0, то пряма збігається з віссю у.

Нагадаємо, що пряма проходить перпендикулярно до вектора .

Геометричним образом лінійного рівняння є пряма на площині. Змінні х та у, що входять до рівняння, — це координати множини точок, що лежать на цій прямій. Якщо поділити рівняння прямої на один з відмінних від нуля коефіцієнтів А, В, С, то це рівняння буде залежати від двох параметрів, що визначають розміщення лінії відносно прямокутної системи координат.

Наприклад, якщо поділимо на , то одержимо рівнян­ня прямої з кутовим коефіцієнтом: , де ,  — кут нахилу прямої до осі ОХ, b — відрізок, що відтинає пряма на осі OY.

Рівняння , де — координати точки, що лежить на прямій, описує множину прямих, що проходять через задану точку.

Рівняння прямої, що проходить через дві задані точки (х₁, у₁) та (х₂, у₂), можна записати у вигляді:

.

Якщо рівняння прямої подати у вигляді

,

то параметри визначають відрізки, що відтинає пряма на відповідних осях системи координат.

Кут між двома прямими і знаходять за формулою: , з якої можна одержати умову паралельності ( ) і перпендикулярності двох прямих. Відстань від точки до прямої обчислюють за формулою:

.

Приклад 1. Дано рівняння сторін і трикутника АВС. Точка — основа висоти . Записати рівняння медіани АМ, бісектриси AF і висоти AD трикутника, а також знайти кут А.

Знайдемо координати вершини А. Для цього розв’яжемо си- стему рівнянь: , .

Запишемо рівняння висоти , використовуючи рівняння прямої, що проходить через дві точки або . Використовуючи умову перпендикулярності , знайде- мо кутовий коефіцієнт сторони ВС трикутника: . Тоді рівняння сторони ВС можна записати так: або . Знайдемо координати вершин В і С трикутника, розв’язавши відповідно системи рів­нянь:

і

Одержимо: . Основа медіани — це середина відрізка ВС; . Використовуючи рівняння прямої, що проходить через дві точки, одержимо рівняння медіани: . Знайдемо довжини сторін Тоді обчислимо відношення, у якому основа бісектриси поділяє сторону ВС: .

За формулами знайдемо координати основи бісектриси . Рівняння бісектриси запишемо як рівняння прямої, що проходить через задані точки: . Для знаходження кута А визначимо кутові коефіцієнти прямої АС — і прямої АВ — .

Тоді

Приклад 2. Дано трикутник . Знайти відстань від вершини В до медіани, що проходить через точку А.

Знайдемо координати основи медіани: . Запишемо рівняння медіани як прямої, що проходить через дві задані точки: , або . Відстань від точки до медіани знайдемо за формулою: .

Приклад 3. Знайти координати точки, що розташована на віддалі 5 одиниць від прямої і прямої .

Нехай — координати шуканої точки, тоді маємо систему рівнянь:

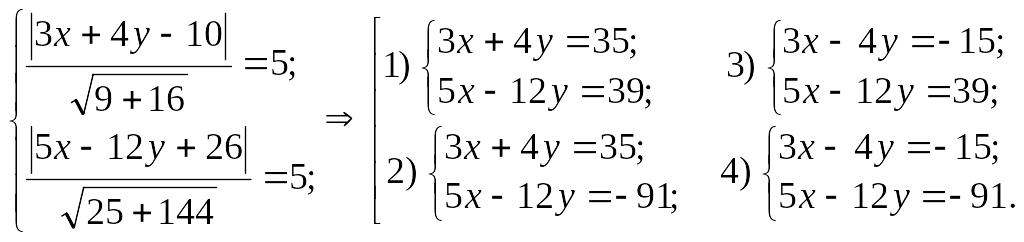
Отже, точок буде чотири:

Приклад 4. Скласти рівняння бісектрис кутів, утворених двома прямими і .

Бісектриса є множиною точок, рівновіддалених від сторін кута. Нехай — одна з точок цієї множини. Тоді, прирівнюючи відстані від цієї точки до прямих, маємо:

.

З останнього рівняння маємо рівняння двох бісектрис у вигляді: і . Слід зазначити, що бісектриси взаємно перпендикулярні: .

Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,

стор.76 – 80.

Тема 6

Кут між двома прямими. Умови паралельності і перпенди-кулярності прямих. Відстань від точки до прямої

Мета заняття: Навчитися знаходити кут між двома прямими, відстань від точки до прямої, застосовувати умови паралельності та перпендикулярності двох прямих при розв'язуванні задач.

Студенти повинні знати: формули обчислення кута між двома прямими, умови перпендикулярності та паралельності двох прямих; формулу відстані між двома векторами.

Студенти повинні вміти: розв'язувати задачи на обчислення косинуса кута між двома векторами і відстані від точки до прямої; застосовувати умови паралельності і перпендикулярності двох прямих при розв'язуванні задач.

Основні питання теми

1.Знаходження кута між двома прямими (різні види завдання прямої);

2.Умови паралельності двох прямих;

3.Умови перпендикулярності двох прямих;

4.Обчислення відстані від точки до прямої

Завдання для самоперевірки

1.Вивести формулу для знаходження відстані точки від прямої.

2.Знайти кут між прямими х = 4 і 2х – у = 0.

3.Точка А(2;0) є вершиною правильного трикутника, а протилежна сторона лежить на прямій х + у – 1 = 0. Скласти рівняння двох інших сторін.

4.Довести, що пряма 3х + 2у – 6 = 0 перетинає відрізок АВ, де А(1;1) і В(2;2).

Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,

стор. 80 – 83.

Лекція ”Кут між прямими”

Розглянемо дві прямі, які задано рівняннями

. (1)

Якщо прямі паралельні, то вони мають однакові кути нахилу:

(2)

Дві прямі збігаються, якщо k1 = k2, b1 = b2.

Якщо прямі взаємно перпендикулярні, то і

.

Рівність є умовою перпендикулярності двох прямих виду (1).

(3)

Якщо прямі не паралельні, то вони перетинаються в точці М(х, у), координати якої є розв’язком системи рівнянь

Нехай  — кут між цими прямими (рис. 1).

Рис. 1

Згідно з рис. 1 маємо: ₂ = ₁ +  (зовнішній кут трикутника дорівнює сумі двох внутрішніх кутів, не суміжних з ним). Отже,

Формулу застосовують для знаходження кута між двома прямими, заданими рівняннями виду (1).

(4)

У трикутнику з вершинами А(1, 1), В(5, 1), С(2, 4) знайти кут  при вершині А, а також рівняння висоти CD і медіани ВМ (рис. 2).

Рис. 2

Скориставшись (3), знайдемо кутові коефіцієнти прямих АВ, АС:

Пряма СD перпендикулярна до прямої АВ. Її кутовий коефіцієнт , а відповідне рівняння

у – 4 = – 4(х – 2).

Точка М поділяє відрізок АС пополам. Отже,

Через точки В(5, 2), М проводимо пряму m і згідно з (4) дістаємо:

або . 

Взаємне розташування двох прямих

Дві прямі задано їх загальними рівняннями:

(1)

Точку перетину М(х, у) цих прямих знаходимо, розв’язуючи систему рівнянь (1), оскільки координати х, у точки М задовольняють одночасно обидва ці рівняння.

Кут  між даними прямими дорівнює куту між їх нормалями (рис. 3).

Рис. 3

Отже, маємо такі залежності:

— умова паралельності прямих.

(2)

Якщо прямі збігаються, то їх коефіцієнти пропорційні:

— умова перпендикулярності прямих.

(3)

Скориставшись формулою скалярного добутку векторів, знай­демо кут :

(4)

Розглянемо спосіб побудови прямих, що проходять через точку перетину двох даних прямих.

Теорема 2. Якщо прямі (1) не паралельні, то рівняння

(5)

визначає пучок прямих, які проходять через точку перетину прямих (1). Вибором  можна дістати будь-яку пряму, що проходить через точку перетину прямих (1), крім другої прямої.

Доведення. При кожному значенні  рівняння (5), що є лінійним, визначає деяку пряму. Припустимо, що коефіцієнти при х, у перетворюються на нуль:

Тоді виконується рівність

а це означає, що прямі (1) паралельні.

Нехай М₀(х₀, у₀) є точкою перетину прямих (1):

Звідси випливає, що

тобто пряма (5) проходить через точку М₀(х₀, у₀).

Візьмемо тепер довільну точку площини М₁(х₁, у₁) і виберемо  так, щоб пряма (5) проходила через точку М₁. Для цього має виконуватися рівність

з якої завжди можна визначити  за умови

.

Іншими словами, точка М₁ не повинна лежати на другій прямій (1). Отже, і справді вибором параметра  можна дістати будь-яку пряму, що проходить через точку перетину прямих (1), за винятком другої прямої (1).

Теорему доведено. 

М аємо рівняння сторін трикутника:

Знайдемо рівняння його висоти, проведеної з вершини С.

● Складемо рівняння пучка променів, які проходять через вершину С:

Далі за умовою (3) перпендикулярності прямих до АВ маємо:

Звідси знаходимо значення  = 4 і рівняння висоти 2х + у – 7 = 0. 

Відстань від точки до прямої

Дано загальне рівняння прямої

Ах + Ву + С = 0 (1)

і точку М₁(х₁, у₁). Знайдемо відстань d від точки М₁ до прямої (1). Візьмемо точку М₀(х₀, у₀) на цій прямій.

Тоді відстань від точки М₁ до прямої дорівнює проекції вектора на вектор нормалі (рис. 4).

Рис. 4

Записуємо аналітичний вираз для шуканої відстані:

Оскільки – Ах₀ – Ву₀ = С, то остаточно маємо:

(2)

Означення. Рівняння виду

(3)

називається нормальним рівнянням прямої (1). Знак перед радикалом має бути протилежний знаку вільного члена С. Якщо С = 0, то вибір знака значення не має.

Узявши в нормальному рівнянні (3)

запишемо його у вигляді

де  — кут між віссю х і вектором нормалі n; р — відстань від прямої до початку координат (рис. 5).

Рис. 5

Перейдемо до полярних координат, скориставшись рівностями х = r cos, у = r sin. Тоді нормальне рівняння прямої набере вигляду

Залежність, записану формулою (2), можна сформулювати як теорему.

Теорема 3. Для того щоб знайти відстань d від точки М₁(х₁, у₁) до прямої, заданої рівнянням (1), достатньо підставити координати точки х = х₁, у = у₁ у нормальне рівняння прямої і знайти модуль здобутої величини.

О бчислити відстань d від точки М₁(5, 3) до прямої 3х + 4у + 3 = 0.

 За формулою (2) знаходимо



Нехай маємо загальні рівняння двох прямих, що перетинаються:

(4)

Якщо точка М(х, у) лежить на бісектрисі кутів, утворених прямими (4), то вона однаково віддалена від цих прямих, тобто виконується рівність:

. (5)

З найти рівняння бісектриси АD трикутника з вершинами А(1, 1), В(6, 3), С(2, 5) (рис. 6).

Рис. 6