Тема 12
Задачі, що приводять до поняття похідної. Означення похідної. Фізичний та геометричний зміст похідної. Таблиця похідних. Похідна складеної та оберненої функцій
Мета заняття Узагальнити та систематизувати знання про похідну, виховувати вміння самостійно відпрацьовувати тему, розвивати логічне мислення.
Студенти повинні знати: означення похідної функції в точці, фізичний та геометричний зміст похідноїї; таблицю похідних основних елементарних функцій; основні формули диференціювання.
Студенти повинні вміти: знаходити похідні за означенням та за таблицею; користуватися правилами диференціювання.
Основні питання теми
1.Задачі, що приводять до поняття похідної (задача про миттєву швидкість руху точки, миттєву силу струму і т.п.); фізичний зміст похідної функції в точці;
2.Означення похідної функції в точці;
3.Геометричний зміст похідної функції в точці;
4.Таблиця похідних;
5.Похідна складеної функції;
6.Похідна оберненої функції
7.Приклади.
Свої набуті знання ви можете перевірити в наступному тесті
1.Якщо існує границя відношення прирісту функції до прирісту аргумента, коли приріст аргумента наближається до нуля, то значення цієї границі називається........
а)границею функції в точці б)неперервністю функції в точці
в)похідною функції в точці г)первісною функції в точці
2.Знаходження похідних від функції f(х) називається......
а)зростанням функції б)спаданням функції
в)інтегруванням функції г)диференціюванням функції
3.Швидкість в даний момент часу - це..........зміст похідної.
а)фізичний б)геометричний
в)алгебраїчний г)механічний
4.Якщо функція описує деякий фізичний процес, то її похідна - є миттєвою швидкістю зміни процесу. В цьому полягає .............. зміст похідної.
а)фізичний б)геометричний
в)алгебраїчний г)механічний
5.Кутовий коефіцієнт дотичної до кривої у=f(х) в даній точці є ...
а)інтегралом функції f(х) б)похідною функції f(х)
в)приростом функції f(х) г)первісною функції f(х)
6.Тангенс кута нахилу дотичної до кривої у=f(х) в даній точці є ..
а)інтегралом функції f(х) б)похідною функції f(х)
в)приростом функції f(х) г)первісною функції f(х)
7.Граничне положення січної КМ, коли точка М по графіку функції у=f(х) наближається до точки K називається....
а)первісною функції в точці К
б)похідною функції в точці К
в)нормаллю до графіка функції в точці К
г)дотичною до графіка функції в точці К
8..Пряма, що проходить перпендикулярно дотичній до графіка функції в точці дотику називається....
а)первісною функції б)похідною функції
в)нормаллю функції г)дотичною функції
9.Похідна сталої функції...
а)не існує б)дорівнює 0
в)дорівнює соs х г)дорівнює sin х
10.Похідна суми двох функції...
а)не існує б)дорівнює 0
в)дорівнює сумі похідних г)дорівнює добутку похідних
Завдання для самоперевірки
1.Як знайти похідну, виходячи з її означення?
2.Довести, користуючись означенням, що
(3х2 – 5х + 2)' = 6х – 5;
3.Дати означення диференційованої функції в точці і на проміжку.
4.Який клас функцій ширший: неперервних в точці х = х0 чи диференційовних в цій точці? Навести приклади.
5.
Нехай витрати виробництва є функцією
кількості випущеної продукції:
.
Знайти
середні і граничні витрати виробництва
за обсягу випущеної продукції, що
дорівнює 10 грошовим одиницям.
6.
Обсяг виготовленої продукції у
(ум. од.) цеху протягом робочого дня
виражається такою функцією
,
де t
— кількість
годин роботи. Знайти обсяг випуску
продукції через 2 години після початку
робочого дня.
7.
У якій точці дотична до параболи
:
1) паралельна осі ОХ;
2) утворює кут 45
з віссю ОХ?
8.
У яких точках кутовий коефіцієнт дотичної
до параболи
дорівнює 3?
9.
Під якими кутами перетинаються парабола
і пряма
?
10.
Під яким кутом перетинаються гіпербола
і парабола
?
11.
Скласти рівняння дотичних до кривої
:
1) в точці ;
2) в точці перетину з віссю OY.
12.
Задано криву
.
Скласти рівняння дотичних:
1)
в точках перетину її з прямою
;
2) паралельної і перпендикулярної до цієї прямої;
3)
що проходять через точку
.
13.
Скласти рівняння спільних дотичних до
кривих
і
.
14.Знайти похідні функцій:
1.
. 2.
.
3.
. 4.
.
5.
. 6.
.
Для кращого засвоєння цієї теми можна порадити виконати завдання на сторінках 203, 218.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор. 191 – 218.
Лекція „Похідна”
Під час вивчення економічних понять, таких, наприклад, як попит, витрати виробництва, національний прибуток, часто доводиться визначати швидкість зміни значень відповідних величин. Розв’язуючи такі задачі, застосовують методи диференціального числення.
Поняття похідної
Нехай у = f(x) є неперервна функція аргументу х, визначена на інтервалі (a, b). Візьмемо деяке значення незалежної змінної х і надамо її деякого приросту х. Тоді функція y = f(x) набуде приросту
у = f(x + x) – f(x) (рис. 1).
Означення.
Відношення
приросту у
функції у
= f(x)
до приросту
незалежної змінної х
називається диференціальним
відношенням:
(1)
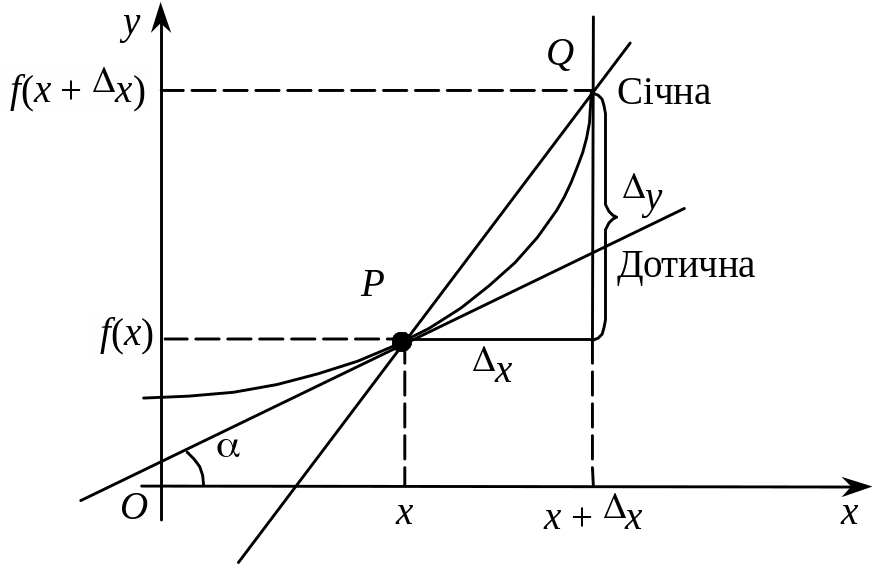
Рис.1
Відношення
є тангенсом кута нахилу січної до осі
Ох.
При
січна прямує до дотичної в точці Р.
Тангенсом кута
нахилу дотичної до осі Ох
при цьому буде границя відношення
.
Означення.
Функція у = f(x) називається диференційовною в точці х = х0, якщо існує границя
|
(2) |
.Значення границі при цьому називається похідною функції у = f(x) у точці х0 і позначається
П
означення.
=
Означення. Функція називається диференційовною на інтервалі І, якщо вона диференційовна в кожній точці х цього інтервалу.
Кожному значенню х із області диференційовності функції f (x) ставиться у відповідність її похідна в точці х. Отже, дістаємо похідну функцію, яку позначаємо f (x). Дія відшукання похідної функції f (x) називається диференціюванням.
Р
озглянемо
функцію
і знайдемо диференціальне відношення
та похідну цієї функції.
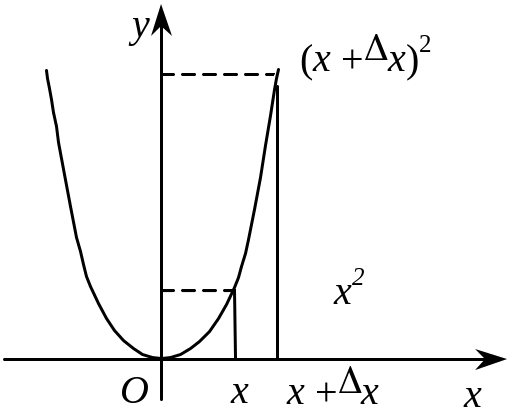
Рис. 2
Диференціальне відношення визначаємо за формулою (1):
.
Похідну
знаходимо за (2):
.
Похідні основних елементарних функцій
1. Похідна степеневої функції
.
Диференціальне відношення (1) має такий вигляд:
.
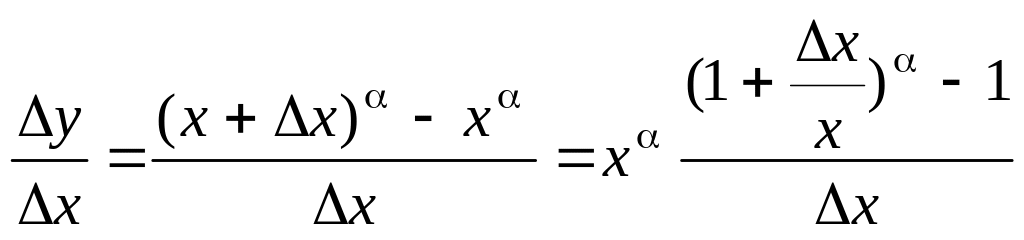Згідно з наслідком 5 маємо:
.
Отже,
=
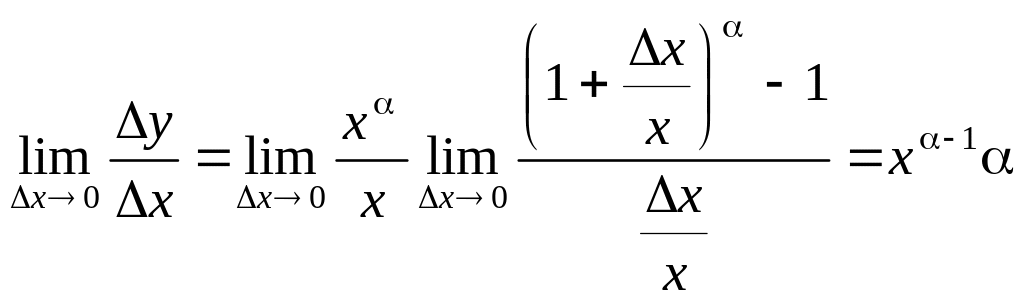
2. Похідна показникової функції
Диференціальне відношення (1) дорівнює
.
Згідно з наслідком 4 маємо:
.
Отже,
.
У частинному випадку при а = е дістаємо:
.
3. Похідна логарифмічної функції
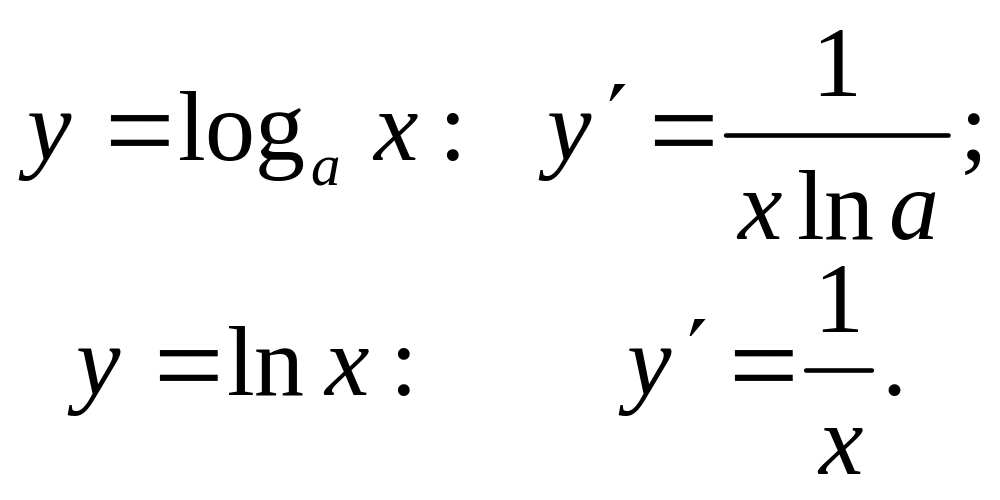
Записуємо диференціальне відношення (1):
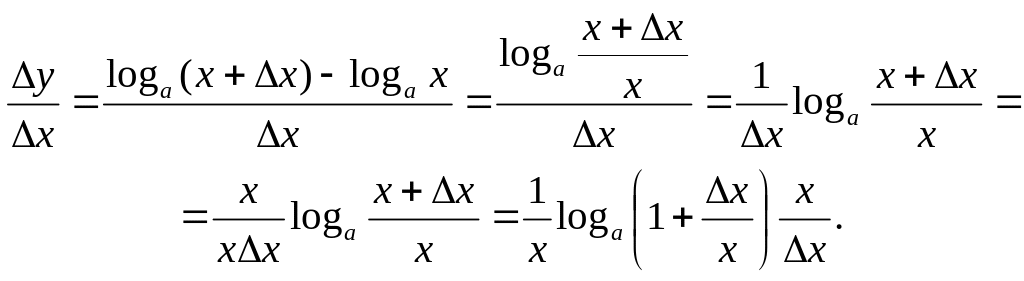
Користуючись другою визначною границею, дістаємо
.
Отже,
при
шукана похідна подається так:
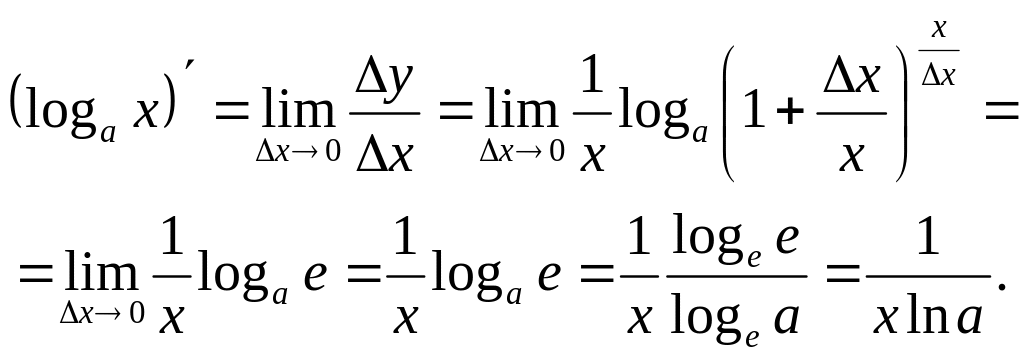
Зокрема, коли а = е, маємо:
.
4. Похідні тригонометричних функцій
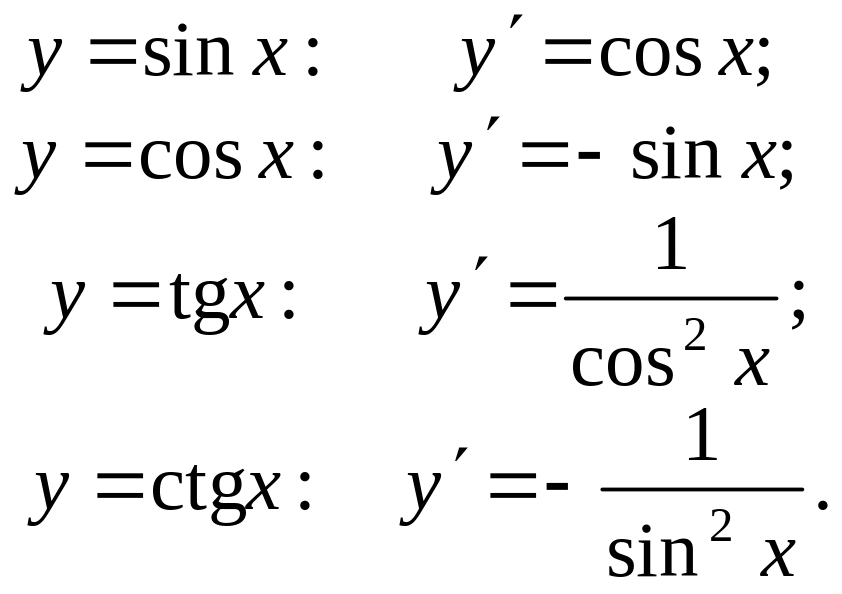
1. Для функції у = sinx диференціальне відношення (1) подається так:
.
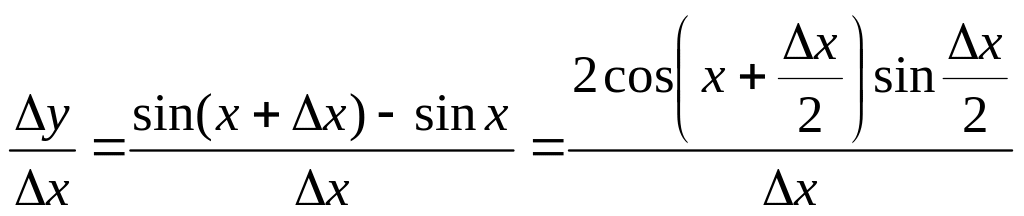Згідно з першою визначною границею маємо:
.
Отже,
.
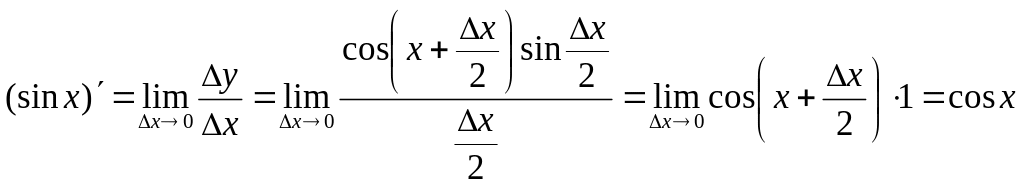2. Аналогічно для функції у = cosx дістаємо:
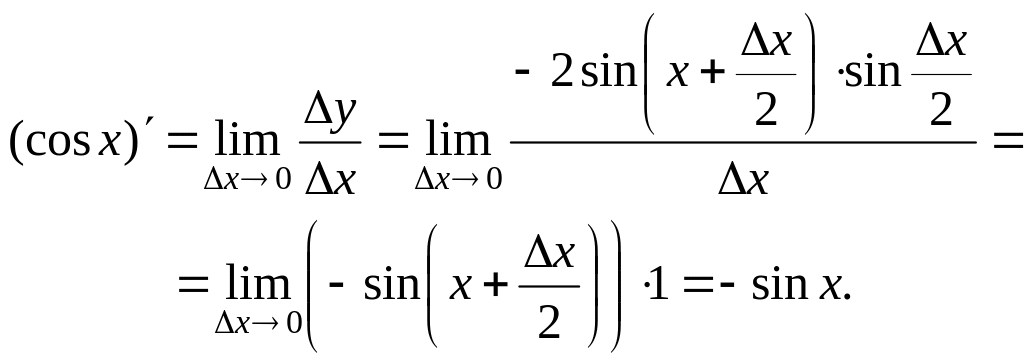
3. Для функції у = tgх диференціальне відношення (1) набуває вигляду:
Згідно
з наслідком 1
.
Отже,
.
4. Аналогічно для функції у = ctgx записуємо:
Правила диференціювання
-
Правило 1. Похідна сталої дорівнює нулеві
(сonst) = 0.
(рис.
3).
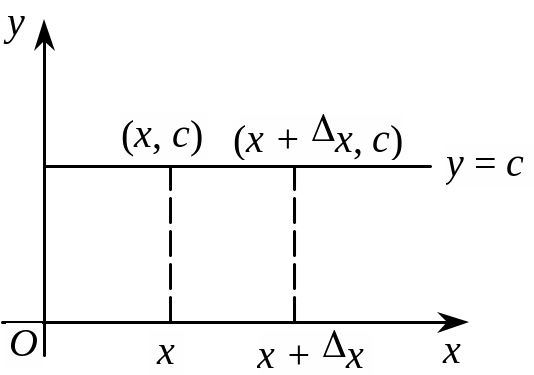
Рис. 3
( 7) = 0; (– 100) = 0.
-
Правило 2. Якщо u — будь-яка диференційовна функція від х і с — довільна стала, то (cu) = cu.
Правило 3. Якщо u та v — диференційовні функції від х, то їх сума u + v є диференційовною функцією:
Аналогічно, похідна суми будь-якого скінченного числа диференційовних функцій дорівнює похідним цієї функції:
|
.
. Нехай у = u + v. Якщо u і v — прирости функцій u та v відносно приросту х аргументу х, то приріст функції у такий:
.
Остаточно маємо:
З
найти
похідну функції
.
.
-
Правило 4. Добуток двох диференційовних функцій u та v є диференційовною функцією
.
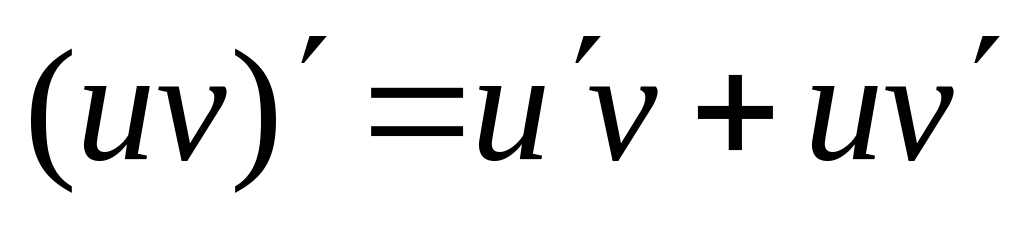Нехай у = uv, де u і v — диференційовні функції від х; ∆х — приріст аргументу х; u і v — прирости u і v. Тоді приріст функції у буде такий:
(рис.
4).
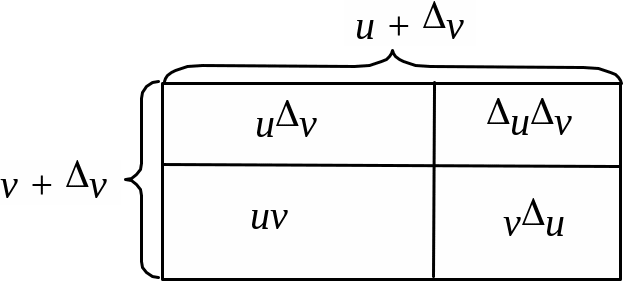
Рис. 4
Отже,
.
Коли х прямує до нуля, маємо:
.
Тоді
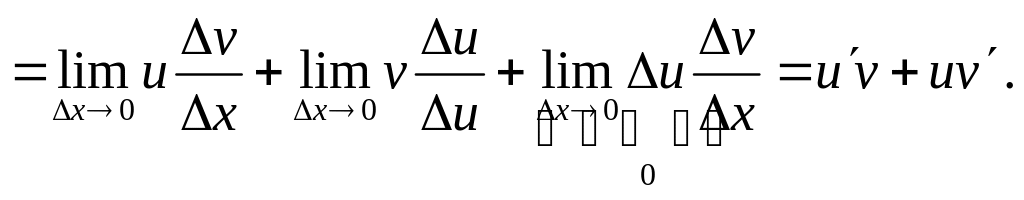
Похідна добутку n функцій:
(3)
З найти у, якщо у = (х2 +1) lnx.
.
Правило
5. У точках,
в яких
|
,
відношення
двох диференційовних функцій є
функція диференційовна, причому
. Розглянемо точки, в яких виконуються умови: ; u i v — диференційовні.
Нехай х набуває приросту х; у, u, v — відповідні прирости функцій у, u і v.
Якщо
в точці х,
,
коли х
близьке до нуля. Тоді виконується
рівність
.
Віднімаючи від неї вираз , дістаємо:
,
або
.
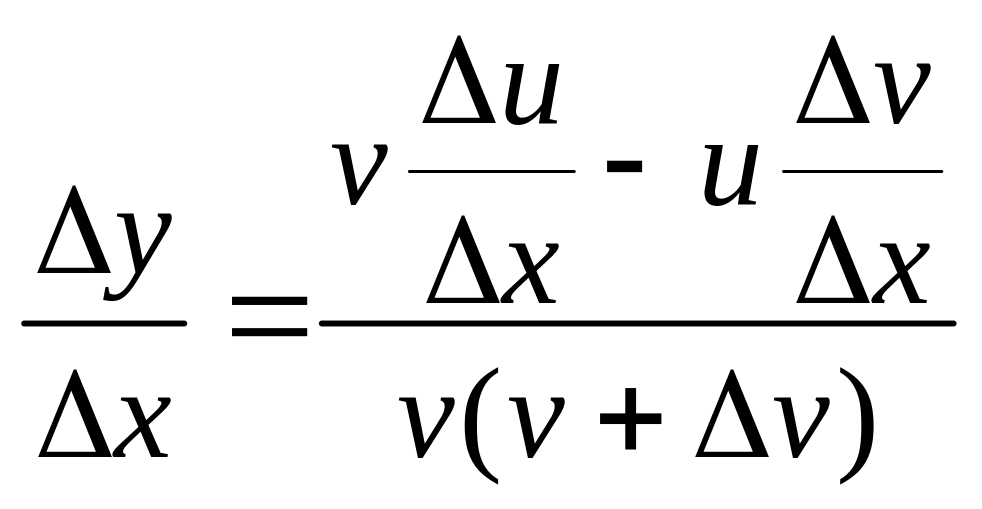Якщо х прямує до 0, маємо:
.
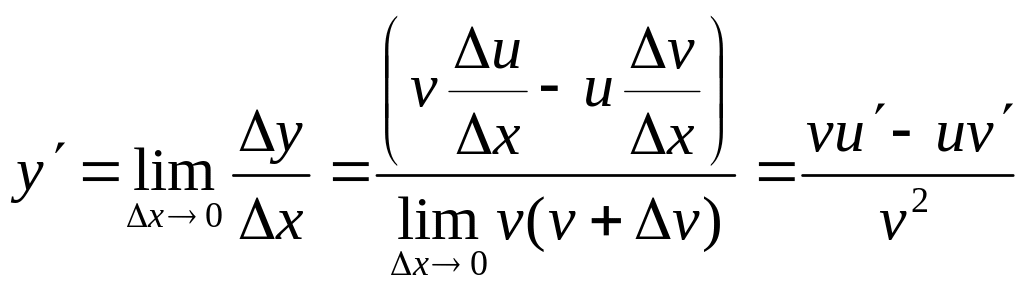З
найти
у,
якщо
.
.
Похідна оберненої функції
Теорема 1. Якщо функція у = f(x) монотонна й має в точці х відмінну від нуля похідну, то функція, обернена до даної, подається у вигляді х = g(y) і має похідну х = g(y), обернену до похідної даної функції:
. (4)
Похідні обернених тригонометричних функцій:
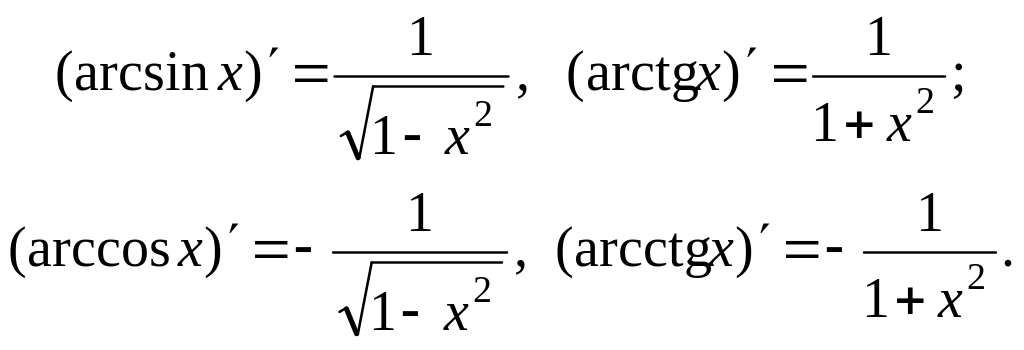
Якщо
,
то для функцій
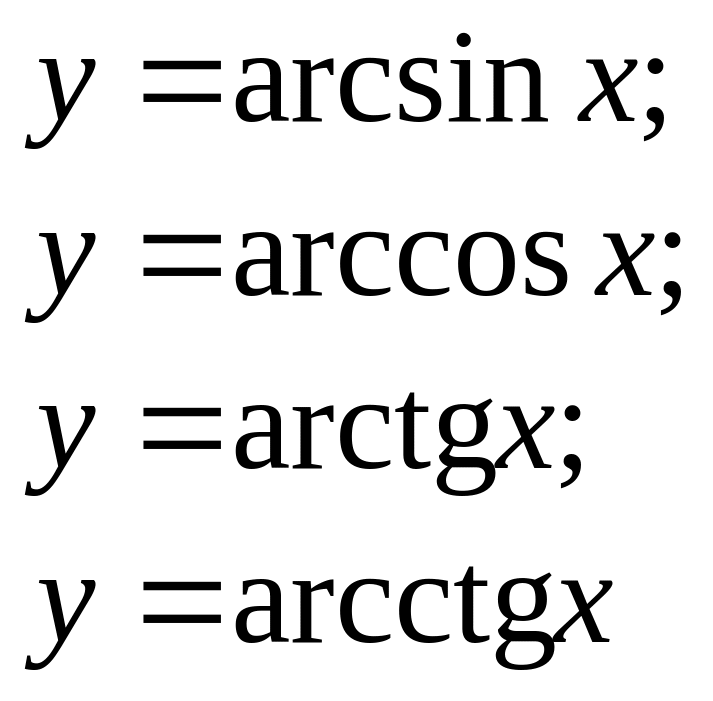оберненими є відповідно такі:
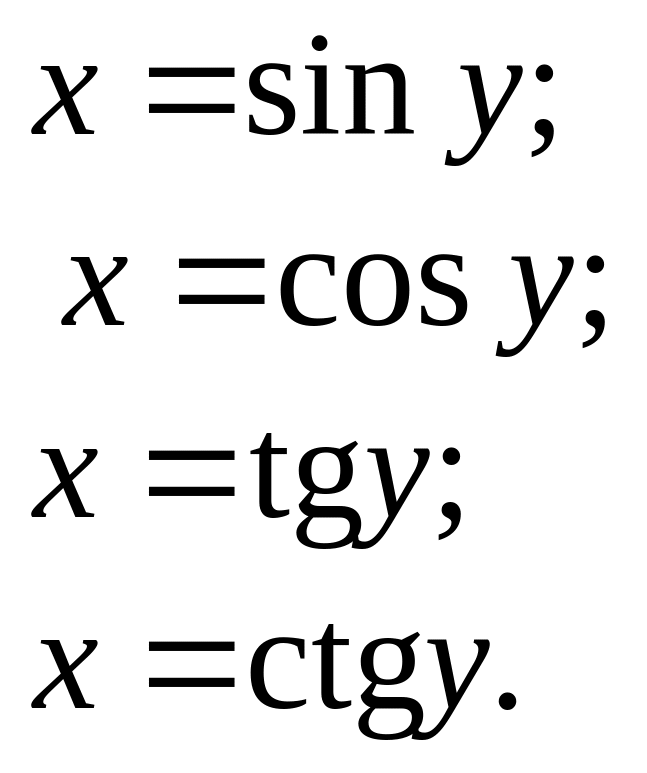
За теоремою 1 маємо:
;
;
;
.
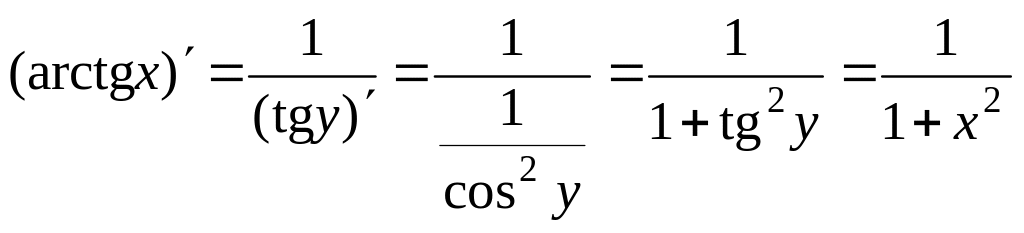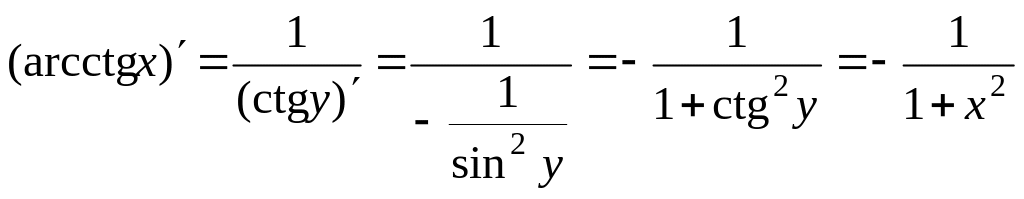Похідна складної функції
Правило 6. |
Теорема 2.
Похідна
складної функції
правило ланцюга. |
:
—
Доведення. Позначимо u = (х). Тоді у = f(u). Знайдемо прирости функцій у = f(u), u = (x):
Далі запишемо диференціальне відношення (1):
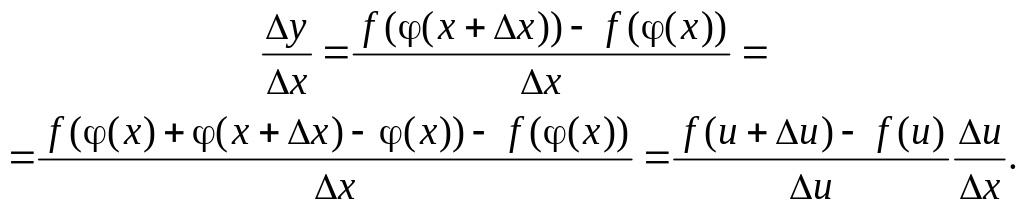
Коли
то
й
.
Тому
.
Задана функція у = f(x). Знайти у.
1)
;
2)
;
3)
.
1) За формулою (5) маємо:
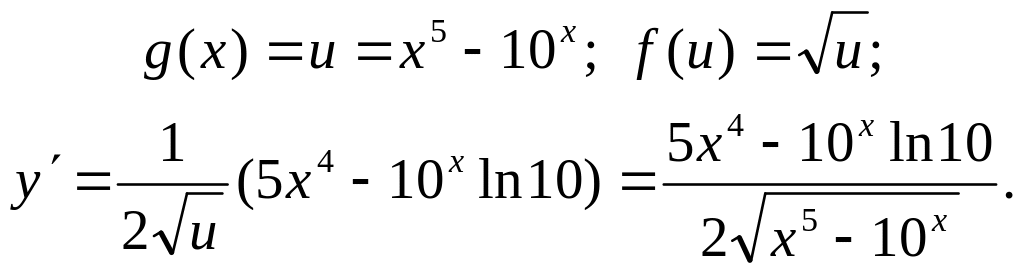
2)
Візьмемо:
.
Тоді за правилом 4
.
Функції
і
—
складні. Згідно з (5) маємо:
.
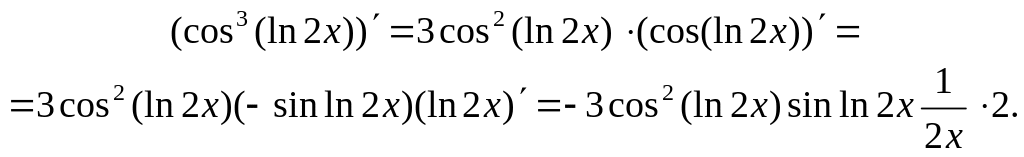
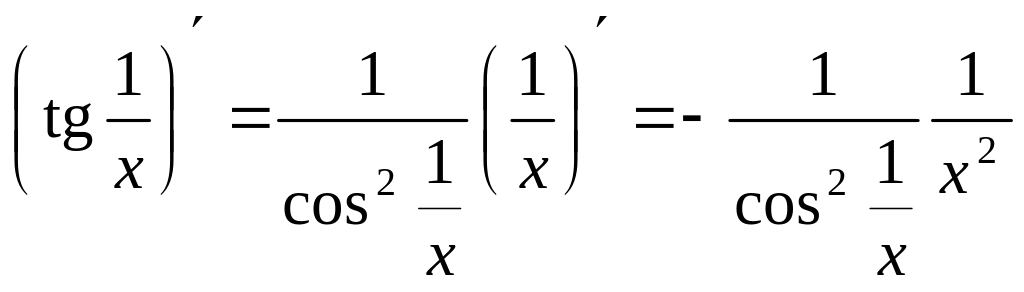3)
Нехай
і
.
Тоді за правилом 5 дістаємо:
.
Похідні
функцій arctgx3
і
обчислюємо за формулою (5):
;
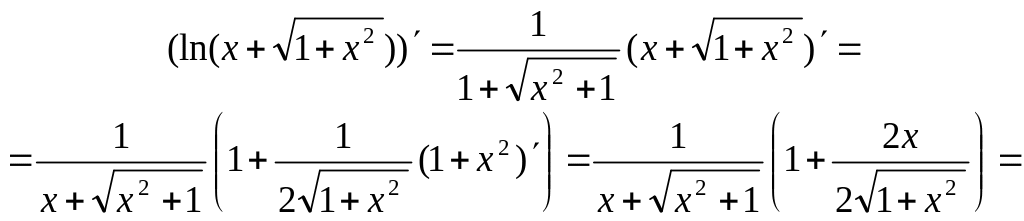
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор. 191 – 218.