
- •Будова математичної теорії Ключові поняття
- •Тема 1:
- •Тема 2 :
- •Тема 3 :
- •Нехай вектор а має початок у точці м1(х1, y1, z1), а кінець — у точці м2(х2, y2, z2). Тоді величини
- •● Згідно з (5) записуємо рівняння двох бісектрис:
- •Умова перпендикулярності площин така:
- •Дві площини збігаються, якщо виконується рівність
- •Тема 9
- •Тема 10
- •Тема 11
- •Основні поняття
- •Тема 12
- •Тема 13
- •Правила обчислення диференціала
- •Формула для знаходження диференціала
- •Тема 14
- •Тема 15
- •Тема 16
- •Тема 17
- •Тема 18
- •Тема 19
- •Тема 20
- •Геометрична інтерпретація
- •Тема 21
- •1 . Обчислення площі фігури у прямокутних координатах
- •2 . Довжина дуги кривої
- •Графічна інтерпретація
- •3. Задача знаходження капіталу за відомими чистими інвестиціями.
- •4 . Деякі задачі, розв’язувані за допомогою теорії інтегралів
- •Тема 22
- •Тема 23
- •Теорема 5. (Теорема Рімана.) Якщо ряд збігається умовно і s — будь-яке наперед задане число, то завжди можна переставити члени ряду так, щоб сума отриманого ряду дорівнювала s.
- •Тема 24
Тема 1:
Визначники 3-го, n-го порядку. Властивості визначників.
Розклад визначника за елементами рядків та стовпців
Мета теми:вивчити поняття визначника третього порядку,-го порядку, їх властивості. Навчитися користуватися теоремою про розкладання визначника.
Студент повинен знати: означення визначника третього та n порядків, властивості; теорему про розкладання визначника.
Студент повинен вміти:обчислювати визначники другого, третього та четвертого порядків; застосовувати теорему про розкладання визначника за елементами рядків та стовпчиків для обчислювання визначників.
Основні питання теми
При вивченні цієї теми треба спочатку уважно прочитати матеріал, зробити конспект, в якому повинні бути означення визначників, їх властивості та схема їх обчислення. Це зручно зробити за наступним планом:
1.Означення визначника 2,3 та n порядку.
2.Загальний вигляд визначника 2, 3 та n порядку.
3.Властивості.
4.Розкладання визначника за елементами рядків та стовпців.
5.Приклади.
Свої набуті знання ви можете перевірте в наступному тесті.
1.Різниця добутків елементів, що стоять у головній та побічній діагоналях називається...
а)матрицею другого порядку б)визначником другого порядку
в)визначником третього порядку г)квадратною матрицею
2.Якщо рядки визначника замінити відповідними стовпцями, а стовпці рядками, то визначник....
а)дорівнює 0 б)не зміниться
в)збільшить порядок г)поміняє знак на протилежний
3.Якщо у визначника поміняти місцями 2 рядка або стовпчика, то він...
а)буде дорівнювати 0 б)не зміниться
в)збільшить порядок г)змінить знак на протилежний
4.Якщо один з рядків визначника (або стовпчиків) складається з нулів, то він...
а)буде дорівнювати 0 б)не зміниться
в)збільшить порядок г)змінить знак на протилежний
5.Якщо визначник має 2 однакових рядка або стопчика, то він...
а)буде дорівнювати 0 б)не зміниться
в)збільшує порядок г)змінить знак на протилежний
6.Якщо елементи двох рядків або стовпчиків визначника пропорційні, то він...
а)буде дорівнювати 0 б)не змінюється
в)збільшує порядок г)змінює знак на протилежний
7.Якщо до елементів одного рядка (стовпчика) визначника додати або відняти елементи іншого рядка (стовпчика), або елементи, пропор-ційні до них, то визначник...
а)буде дорівнювати 0 б)не зміниться
в)збільшить порядок г)змінить знак на протилежний
8.Обчислити визначники
Завдання для самоперевірки
Обчислити визначники різними методами:
3 2 4 1 -2 5 -3 4 0 6
1 -4 5 2 1 -3 2 -1 3 2
2 3 1 -1 3 4 4 0 5 1
1 2 3 -5
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001,
стор. 6 – 12.
Лекція „Визначники третього порядку”
Вираз
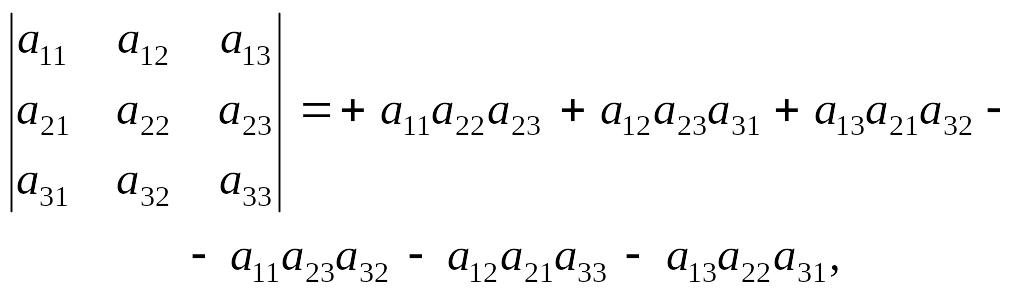
являє собою визначник третього порядку.
Існує простий спосіб розкриття визначника третього порядку — так зване правило Саррюса. Допишемо до визначника (2) перший і другий стовпці, а далі перемножатимемо елементи, що розміщені на одній лінії, як показано на схемі:

Добуток елементів, які розміщені на лініях, що йдуть згори ліворуч униз праворуч, береться зі знаком «+». Добуток елементів, розміщених на лініях, що йдуть згори праворуч униз ліворуч, береться зі знаком «–».
О![]() бчислимо
визначник третього порядку
бчислимо
визначник третього порядку
 .
.
За правилом Саррюса складемо таблицю


і знайдемо значення визначника:
D3 = 1 2 2 + 2 1 3 + 3 2 1 – 3 2 3 – 1 1 1 – 2 2 2 = –11.
Оскільки визначник n-го порядку складається з n! доданків, то формула (1) не застосовується для обчислення визначників при n > 3 (уже при n = 4 визначник містить 4! = 24 доданки).
Для обчислення визначників застосовують властивості, що розглядаються далі.
Властивості визначників
Властивість 1. При транспонуванні визначника його значення не змінюється.
Доведення. Доведемо, що визначники

рівні. Розглянемо доданки, які входять до D:
![]() .
.
Якщо
позначити
![]() ,
то до визначника D1
увійде відповідний доданок
,
то до визначника D1
увійде відповідний доданок
![]() .
.
Оскільки до визначників D та D1 входять однакові доданки з однаковими знаками, то D = D1.
Із властивості 1 випливає, що рядки та стовпці визначника рівноправні. Усі наведені далі властивості, що справджуються для рядків, виконуються й для стовпців.
Д![]() ля
визначника другого порядку маємо:
ля
визначника другого порядку маємо:
![]() .
.
Властивість 2. Якщо всі елементи деякого рядка дорівнюють нулю, то визначник дорівнює нулю.
Доведення. Оскільки кожний із доданків, що входять до визначника, містить нульовий множник, то всі доданки дорівнюють нулю і визначник також дорівнює нулю.

Властивість 3. Якщо всі елементи будь-якого рядка мають спільний множник, то його можна винести за знак визначника.
Доведення. Кожний із доданків, що входять до визначника, містить один із елементів розглядуваного рядка. Тому спільний множник елементів цього рядка можна виносити із суми цих доданків.
О бчислимо визначник:
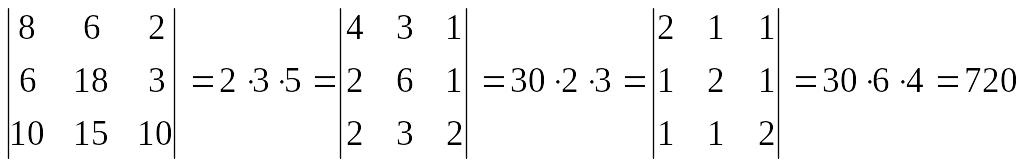 .
.
Властивість 4. Якщо поміняємо місцями два рядки визначника, то він змінить свій знак.
Доведення. У визначнику n-го порядку поміняємо місцями k-й і s-й рядки (s > k). Здобутий визначник позначимо D1. Якщо до визначника D входить доданок
![]() ,
,
то до визначника D1 обов’язково входить аналогічний доданок
![]() .
.
Оскільки переставлення других індексів відрізняються однією транспозицією, то парність переставлень різна. Отже, доданок, що є добутком розглядуваних елементів, завжди входить до в изначників D та D1 з різними знаками. Це й доводить потрібну властивість.
Поміняємо місцями рядки у визначнику:
![]() .
.
Властивість 5. Якщо у визначнику два рядки однакові, то визначник дорівнює нулю.
Доведення. Поміняємо місцями однакові рядки визначника. Він при цьому не зміниться, а згідно з властивістю 4 лише змінить свій знак, тобто D = –D. Звідси випливає, що D = 0.
Д ля визначника третього порядку виконується рівність:
 ,
,
оскільки цей визначник має два однакові рядки.
Властивість 6. Якщо у визначнику елементи одного рядка пропорційні до відповідних елементів іншого рядка, то визначник дорівнює нулю.
Доведення. Винесемо множник пропорційності за знак визначника й дістанемо визначник з двома однаковими рядками, який дорівнює нулю.
Властивість 7. Якщо у визначнику D всі елементи будь-якого рядка є сумою двох доданків, то цей визначник є сумою двох визначників, усі елементи яких (крім фіксованого рядка) збігаються. У першому визначнику фіксований рядок містить перші доданки, у другому визначнику фіксований рядок містить другі доданки.
Доведення. Візьмемо k-й рядок. Оскільки до кожного з доданків, що утворюють визначник, входить один із елементів k-го рядка, то можна в загальному вигляді записати розклад визначника за елементами цього рядка:
![]() .
.
Множники
![]() називаються алгебраїчними
доповненнями елементів
називаються алгебраїчними
доповненнями елементів
![]() .
Якщо
ці елементи є сумами двох
доданків
.
Якщо
ці елементи є сумами двох
доданків
![]() то
то
![]()
![]()
що й доводить сформульовану властивість.
З а властивістю 7 маємо:
 .
.
Властивість 8. Якщо до елементів деякого рядка визначника додати відповідні елементи іншого його рядка, помноживши на одне й те саме число, то значення визначника при цьому не зміниться.
Доведення.
Додамо до елементів k-го
рядка визначника D
елементи s-го
його рядка
![]() ,
помножені на число .
Здобутий визначник набере такого вигляду
D1:
,
помножені на число .
Здобутий визначник набере такого вигляду
D1:
![]()
Останній доданок дорівнює нулю, бо визначник має однакові k-ті та s-ті рядки. Отже, D1 = D.
М аємо рівність визначників:
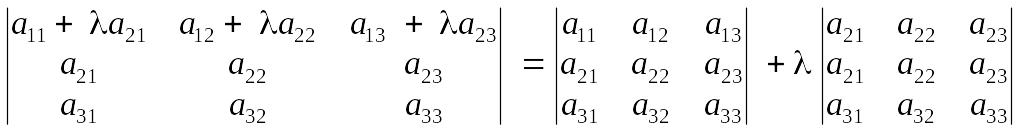 .
.
Із доведення властивостей 7 і 8 випливають розглянуті далі властивості визначників.
Властивість 9. Сума добутків елементів будь-якого рядка або стовпця визначника на відповідні алгебраїчні доповнення дорівнює цьому визначнику, тобто якщо
 ,
,
то справджуються рівності:
![]()
Властивість 10. Сума добутків елементів будь-якого рядка визначника на алгебраїчне доповнення відповідних елементів іншого його рядка дорівнює нулю:
![]() .
.
Аналогічна властивість виконується для стовпців:
![]() .
.
О бчислимо визначник четвертого порядку
 .
.
Додамо перший рядок до другого і четвертого, утворивши визначник
 .
.
Поміняємо місцями перший і третій стовпці:
 .
.
Додамо другий рядок до третього і четвертого рядків і винесемо спільний множник елементів третього і четвертого рядків:
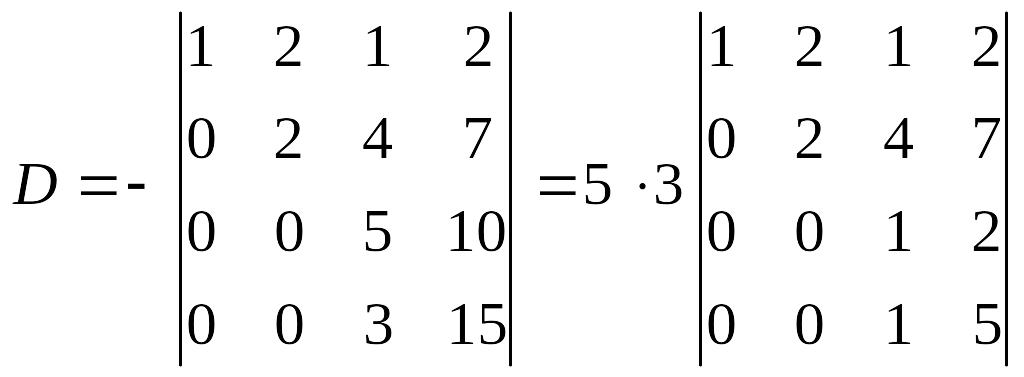 .
.
Віднявши третій рядок від четвертого, обчислимо даний визначник за формулою (1):
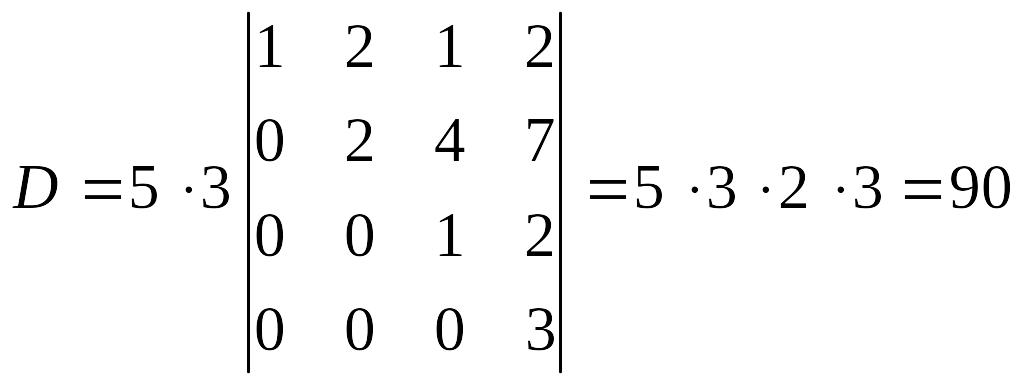 .
.
Література : В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001
