Додаток 2
Практичне заняття
Тема: Алгебри. Типи алгебри.
Мета: сформувати поняття алгебри, групи, півгрупи, кільця, підкільця, дослідити базові півгрупи, групи, сформувати вміння доводити замкненість множини відносно операції та відносно оберненого елемента, використовувати означення групи та кільця.
Хід заняття
Запитання для повторення та актуалізації знань.
Що називають алгеброю? Алгебраїчною системою називають . . .
Що називають типом алгебри?
Назвати найпростіші алгебри. Вказати їх типи. Навести приклади.
Вказати алгебри, відомі з шкільного курсу математики..
Півгрупою називається. . .
Доведіть, що множина натуральних парних чисел утворює півгрупу по додаванню.
Обґрунтуйте той факт, що множина натуральних парних чисел не є півгрупою відносно операції віднімання.
Множина А називається групою якщо . . .
В якому випадку елемент е називається нейтральним? При визначені яких алгебраїчних структур він використовується? Навести приклади.
Елемент
 називається симетричним до а,
якщо . . . Навести приклади.
називається симетричним до а,
якщо . . . Навести приклади.Підгрупа –це. . . Назвати ознаку підгрупи.
Кільцем називають . . .
Підкільцем називають . . .Назвати ознаку підкільця.
Завдання для аудиторної роботи:
Для початку наведемо приклади півгруп, які відомі зі школи:
Адитивні
(по додаванню) – ![]()
Мультиплікативні(
по множенню) - ![]()
Задача
1:
Чи утворює множина ![]() півгрупу відносно операції множення.
півгрупу відносно операції множення.
Правило-орієнтир:
Перевірити чи є задана операція алгебраїчною в даній множині;
В разі позитивної відповіді перевірити чи є дана операція асоціативною.
Розв’язання:
![]()
Отримана
рівність виконується для будь-яких
чисел ![]() і
і ![]() .
Результат належить множині
.
Таким чином задана операція є алгебраїчною.
Говорять, що множина
.
Результат належить множині
.
Таким чином задана операція є алгебраїчною.
Говорять, що множина ![]() замкнена
відносно операції множення.
замкнена
відносно операції множення.
Оскільки, числа з множини
 є дійсними, а операція множення є
традиційною в
є дійсними, а операція множення є
традиційною в  ,
то перевіряти асоціативність не має
потреби, вона має місце.
,
то перевіряти асоціативність не має
потреби, вона має місце.
Отже, утворює мультиплікативну півгрупу.
Вправи на закріплення:
Які з наступних підмножин множини
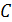 є мультиплікативними півгрупами:
є мультиплікативними півгрупами:
 ;
;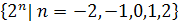 ;
;{-1,0,1}
Довести, що множина
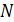 є
півгрупою за вказаною операцією:
є
півгрупою за вказаною операцією:
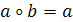 ;
; ;
;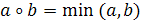 .
.
Вказівка: нейтральний елемент по додаванню називають нульовим, по множенню – одиничним; симетричний елемент по додаванню називають протилежним, по множенню – оберненим.
Задача
2:
Довести, що множина ![]() утворює адитивну групу.
утворює адитивну групу.
Добре відомими, з школи, прикладами алгебраїчних структур є такі числові множини з традиційними операціями додавання та множення:
N – множина натуральних чисел;
![]() множина цілих невід’ємних чисел;
множина цілих невід’ємних чисел;
- множина цілих чисел;
Q – множина раціональних чисел;
R – множина дійсних чисел.
Множини
,
Q, R
утворюють абелеві групи відносно
додавання. Числові множини ![]() ,
,
![]() є абелевими групами відносно множення.
є абелевими групами відносно множення.
Правило – орієнтир:
Перевірити замкненість множини відносно операції;
Вибрати шлях доведення: за означенням, чи за ознакою;
За означенням перевіряємо:
1) чи є операція асоціативною;
2) чи містить дана множина нейтральний елемент;
3) визначаємо симетричний елемент для кожного елемента множини;
4. За ознакою перевіряємо:
1) чи є дана множина підмножиною множини відомої групи;
2) чи замкнена задана множина відносно операції, що визначена в
групі;
3) чи замкнена дана множина відносно симетричного елемента.
Розв’язання задачі 2:
Множина
є підмножиною множини ![]() ,
яка є групою по додаванню. Тому доведення
зручно проводити за ознакою:
,
яка є групою по додаванню. Тому доведення
зручно проводити за ознакою:
Перевіримо замкненість по додаванню в

![]()
Отримане число належить множині , отже, множина замкнена відносно додавання.
Знайдемо симетричний елемент
![]()
![]()
![]()
![]()
Отримане
число ![]() є елементом множини
,
тобто задана множина є замкненою відносно
симетричного елемента.
є елементом множини
,
тобто задана множина є замкненою відносно
симетричного елемента.
Висновок:
![]() - група.
- група.
Запитання для закріплення
Чи є множина
 - абелевою групою?
- абелевою групою?Чи є множина
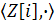 - групою?
- групою?
Вправи на закріплення:
У множині всіх пар
 раціональних чисел операція множення
визначена рівністю
раціональних чисел операція множення
визначена рівністю 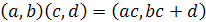 . Довести, що задана алгебра є групою.
(за означенням)
. Довести, що задана алгебра є групою.
(за означенням)Довести, що наступні множини чисел є адитивними групами (за ознакою):
 ;
;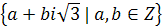 ;
;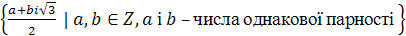 .
.
Запитання для закріплення
На множині
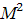 ,
М – деяка множина, визначена операція
,
М – деяка множина, визначена операція
 по правилу:
по правилу: 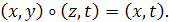 Чи є
півгрупою? Групою?
Чи є
півгрупою? Групою?Наведіть приклад множини з введеною на ній операцією, що не є півгрупою.
Задача 3: Перевірити, чи утворює множина - кільце відносно
традиційних операцій додавання та множення.
Означення
1:
Бінарна операція
є дистрибутивною відносно операції
![]() ,
якщо
,
якщо![]()
![]()
З школи відомо, що в множинах N, , Q, R операція множення є дистрибутивною відносно операції додавання.
Правило – орієнтир:
Перевірити чи задана множина є замкнена відносно традиційних операцій додавання та множення дійсних чисел;
Вибрати шлях доведення: за означенням чи за ознакою;
За означенням перевірити:
Чи є дана множина абелевою групою по додаванню, тобто перевірити:
А) чи є операція додавання асоціативною, комутативною;
Б) чи містить дана множина нульовий елемент;
В) визначити протилежний елемент для кожного елемента множини;
Чи є дана множина півгрупою по множенню, тобто чи є операція множення асоціативною;
Чи виконуються дистрибутивні закони;
За ознакою перевірити:
Чи є дана множина підмножиною множини відомого кільця;
Чи замкнена множина відносно додавання, віднімання та множення будь-яких двох елементів множини.
Розв’язання задачі 3:
Дана множина є підмножиною дійних чисел. Отже, доведення будемо проводити за ознакою.
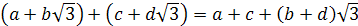 – отримали число з множини
– отримали число з множини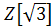 .
. - число належить множині
.
- число належить множині
.Замкненість множення ми перевірили в задачі 1.
Висновок:
![]() - кільце.
- кільце.
Вправи на закріплення:
Перевірити, які з множин з вправи 4 утворюють кільце.
Зауваження: з курсу «Лінійна алгебра» відомо, що множина квадратних матриць утворює кільце відносно введених операцій додавання та множення. Тому в наступному завданні можна перевірку виконувати за ознакою.
Перевірити, які з даних множин утворюють кільце, відносно традиційних операцій додавання та множення.
 ;
; ;
;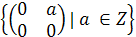 .
.
Запитання для закріплення
Яку умову потрібно додати до означення кільця, щоб множина утворювала комутативне кільце?
Перевірте, чи утворюють комутативні кільця наведені в вправах 5,6.
Означення 2: Кільце К називається кільцем з одиницею, якщо в К існує
нейтральний елемент по множенню.
Задача
4: Довести,
що множина ![]() з наступними операціями є
з наступними операціями є
комутативним кільцем з одиницею:
![]() ,
,
![]() .
.
Розв’язання:
З умови задачі видно, що операції додавання та множення є замкненими на заданій множині.
Додавання елементів даної множини зводиться до додавання цілих чисел,а отже, ця операція є асоціативною та комутативною.
Легко бачити, що
![]() .
Тобто (0,0)- нульовий елемент;
.
Тобто (0,0)- нульовий елемент;
![]() .
Тобто
.
Тобто ![]() - протилежний елемент.
- протилежний елемент.
Отже,
![]() - абелева група.
- абелева група.
Множення елементів даної множини зводиться до множення цілих чисел,а отже, ця операція є асоціативною та комутативною.
Отже,
![]() - комутативна півгрупа.
- комутативна півгрупа.
Таким
чином, ![]() - комутативне кільце.
- комутативне кільце.
Знайдемо одиничний елемент по множенню:
![]()
![]()
![]()
Така
ситуація можлива, якщо ![]() .
.
Висновок: задана множина утворює комутативне кільце з одиницею.
Вправи на закріплення:
Довести, що множина
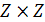 з наступними операціями є
з наступними операціями є
комутативним кільцем з одиницею:
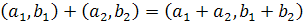 ,
,
![]() ;
;
,
![]() ;
;
,
![]() .
.
Запитання для закріплення
Вказати таке кільце з одиницею, яке не є комутативним.
Завдання для самостійного опрацювання:
Чи є множина комплексних чисел з фіксованим модулем r групою відносно множення.
Чи є множина степенів даного дійсного числа
 з цілими показниками групою відносно
множення.
з цілими показниками групою відносно
множення.Довести, що півінтервал [0,1) з операцією
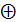 ,
де
,
де  - дробова частина числа
- дробова частина числа 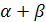 ,
є групою.
,
є групою.Довести, що наступні множини матриць з традиційними операціями додавання та множення є кільцем. Які є комутативними? Які містять одиницю?
 ;
;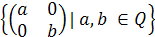 ;
; ;
;
Довести, що наступні з числових множин з звичайними операціями додавання та множення є кільцями:
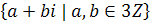 ;
;