Додаток 1

Практичне заняття

Тема: Відношення. Алгебраїчні операції.

Мета: сформувати поняття алгебраїчної операції, відношення, сформувати вміння перевіряти арність відношення, функціональність відношення, алгебраїчність заданої операції.

Хід заняття

Запитання для повторення та актуалізації знань

1. Як пов’язані між собою декартовий добуток, п-арне відношення та п-арна операція?(число п – для п-арне відношення називається «арністю» або рангом відношення.)

2. Яке відношення називається функціональним?

3. Що називається областю визначення п+1-арного відношення?

4. Навести приклади унарних, бінарних та тернарних відношень.

5. Вказати приклад часткової алгебраїчної операції.

6. Як перевірити, чи є операція задана на множині А алгебраїчною?

7. Перевірити, чи є операція 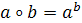алгебраїчною на множині R.

Завдання для аудиторної роботи:

Задача 1: Які з операцій є алгебраїчними на підмножині

множини R; які з алгебраїчних операцій є комутативними,

асоціативними:

1. 

2. 

Правило – орієнтир:

для перевірки, чи є бінарна операція алгебраїчною на даній множині

необхідно:

а) взяти два елементи з цієї множини;

б) виконати операцію за даним правилом над цими елементами;

в) перевірити, чи одержаний результат належить даній множині. Якщо

належить, то операція алгебраїчна, якщо ні - операція не є алгебраїчною.

Вказівка: алгебраїчні операції можуть мати такі властивості:

• асоціативність;

• комутативність.

Добре відомими, з школи, прикладами алгебраїчних структур є такі числові множини з традиційними операціями додавання та множення:

N – множина натуральних чисел;

множина цілих невід’ємних чисел;

- множина цілих чисел;

Q – множина раціональних чисел;

R – множина дійсних чисел.

В наведених вище множинах операції додавання і множення є асоціативними та комутативними. Але операція на множині може бути задана так, що вона не матиме властивостей асоціативності або комутативності (обох разом, або однієї з них).

Означення 1: Бінарна операція називається асоціативною на множині А

якщо:

Означення 2: Бінарна операція називається комутативною на множині А

якщо:

Розв’язання задачі 1:

1)

а)

б)

в) , тобто .

Отже, операція алгебраїчна.

Перевіримо, чи є дана операція асоціативною, комутативною.

А) асоціативність

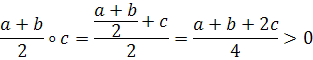
Але можна знайти такі дійсні числа , що

Отже, дана алгебраїчна операція на множині А не є асоціативною.

Б) комутативність

Оскільки, додавання дійсних чисел є комутативною операцією, то . Отже, дана алгебраїчна операція на множині А є комутативною.

2)

а)

б)

в) , тобто

Отже, вказана операція є алгебраїчною.

Перевіримо, чи є дана операція асоціативною, комутативною.

1) асоціативність

Бачимо, що , таким чином, операція на множині А не є асоціативною.

Б) комутативність

Але існують такі числа , що

Отже, задана алгебраїчна операція не є комутативною.

Вправи на закріплення:

1. Які з операцій є алгебраїчними на підмножині множини R; які є комутативними, асоціативними:

2. 

3. 

4. 

Задача 2: Чи є скалярний добуток векторів алгебраїчною операцією в

трьохвимірному евклідовому просторі ? Якщо так, то

перевірити чи є дана операція комутативною, асоціативною.

Розв’язання:

а)

б)

в) при скалярному множенні векторів і з отримуємо число, а не вектор. Отже, скалярний добуток векторів не є алгебраїчною операцією в .

Вправи на закріплення:

2. Вказати, які з наступних операцій є алгебраїчними в . Які з алгебраїчних

операцій комутативні, асоціативні:

А) множення вектора на скаляр;

Б) векторний добуток векторів?

Запитання для закріплення

1. Чи слідує з того, що алгебраїчна операція комутативна її асоціативність?

2. Назвіть приклади алгебраїчних операцій, які є одночасно комутативними,

асоціативними.

3. Перевірити чи операції - додавання, множення, віднімання - є

алгебраїчними в множині .