Относительные измерения силы тяжести

1. Маятниковый метод;

2. Спутниковый метод;

3. Относительное измерение гравиметрами.

1. Маятниковый метод.

О н (метод) основан на наблюдении свободных колебаний одного и того же маятника на разных пунктах.

Пусть на исходном пункте измеряется период измерений

Т₁=π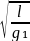

Считается, что известно Т₁ и Т₁²

Т=π

= => g =

При относительных маятниковых определениях: 1)не надо знать точного значения длины маятника; 2)длина маятника должна быть постоянной. Обычно на практике измеряют приращение периода

∆Т=Т – Т₁ ; Т₁=Т - ∆Т ;

g = g₁ ; g = g₁ ; g = g₁(1 - + ) ; g = g₁ + g₁(- + ) ;

g - g₁ = g₁(- + ) ; ∆g = g₁(- + ) ; = - + ( )² .

Можно определить как ∆g, так и относительную величину этого приращения. Достоинством способа является то, что нет необходимости знать ускорение силы тяжести в населённом пункте. Покажем, что не смотря на то, что здесь присутствует g₁ на исходном пункте, с высокой точностью его знать не надо, выполним для этого упрощённый анализ.

= - пренебрегая вторым членом - = ; тогда = c ; ∆g = cg₁ ; m_∆g = cm_g₁ ; = ; m_∆g = m_g₁ .

Зададимся предельной величиной m_∆g=0,01 мгал. Допустим, что приращение силы тяжести может достигать величины порядка 100 мгал (∆g=100 мгал).

g₁ = 9,8 м/сек ; 1 гал = 1 см/сек² ; g₁ = 980 гал = 980 000 мгал

Исходя из m_∆g и g₁, определим с какой точностью необходимо знать m_g₁

m_∆g = ∆g ; 0,01=100 ; m_g₁= 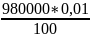= 98 мгал.

В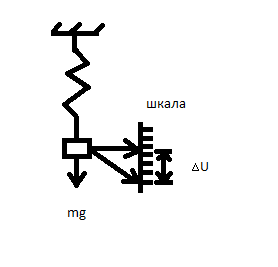 формуле относительного определения силы тяжести присутствуют значения ∆Т и Т, которые необходимо измерять с высокой точностью. В формуле определения силы тяжести абсолютным методом в скобках присутствует член, зависящий от амплитуды колебаний. Очевидно, что в период колебаний необходимо вводить поправки:

- за амплитуду;

- за температуру;

- за плотность окружающей среды;

- за частоту генератора колебаний;

- за влияние кривизны оси колебаний маятника;

- за влияние вибраций штатива и других факторов.

Само измерение периода колебаний осуществляется по их набору или по их большому числу.

Пусть в некоторый момент маятник находится в положении θ₀

С момента Т₀ маятник коснулся целое N раз

τ = t_к – t_н ; N' = N+θ₀+ θ_n , тогда T =

Поскольку поправка за амплитуду самая основная, то необходимо определять ещё и амплитуду колебаний. Амплитуда колебаний определяется из формулы гармонических колебаний.

3. Модель гравиметрического метода определяется приращением силы тяжести. Это можно продиманстрировать на примере пружины. По закону Гука

где – очевидное состояние пружины к которой приложена нулевая сила. Путем дифференцирования найдем зависимость между приращении длины пружины и приращении силы тяжести.

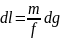
В зависимости от подвески гравиметры могут быть - механические, в зависимости от компенсации mg гравиметры могут быть газовые и электро-магнитные, в которых газ и электромагнитное поле заменяют пружину. На точность гравиметра оказывают влияние следующие факторы: температура, влияющая на упругую среду гравиметра; плотность окружающей среды, наклон гравиметра, микросейсмическое колебание магнитного и электрических полей. Чувствительность гравиметра определяется названными факторами. - это изменение показаний отсчета вызванное изменением силы тяжести. Чувствительность =

Вся конструкция гравиметра должна быть направлена на повышение чувствительности. Повышение чувствительности может осуществляться как учетом названных факторов, так и устройством дополнительных конструктивных элементов. Повышение чувствительности гравиметра с помощью дополнительных устройств, называемых астанированием. Устройства должны быть такими, чтобы они выполняли:

1. Свои конструктивные функции

2. Повышали чувствительность гравиметра

Пусть на некой опоре коромысла с двумя одинаковыми массами g₁ и g₂ с его помощью определяют приращение ∆g.

Это есть принципиальная схема вариометра, измеряющего . Коромысла приводит в равновесие с помощью цилиндрического уровня. Пусть при перемещении этой конструкции в другую точку определяется разность g₂ – g₁=∆g. Уровень наклонился, содержимое уровня переместилось в сторону наклона и усилила эффект разности силы тяжести.