21

Вариант 1.

1. Дана задача линейного программирования:

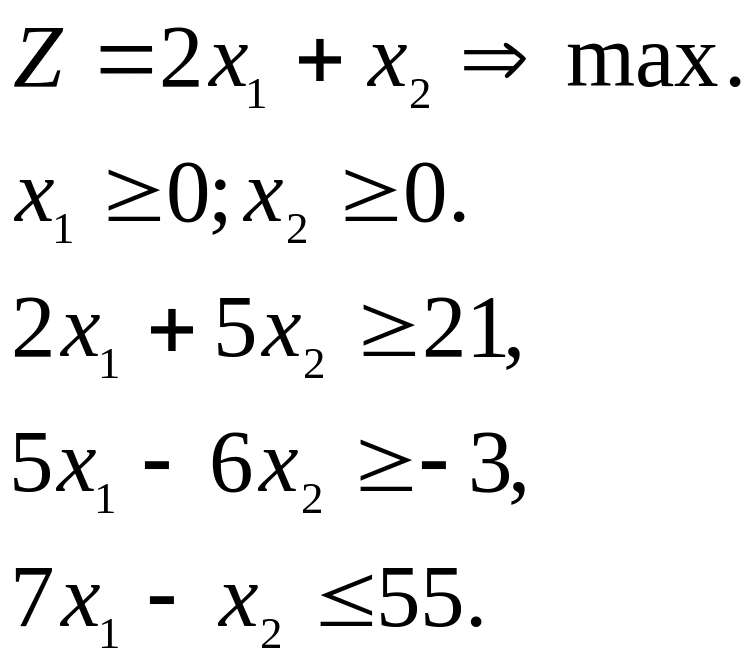
а) Решить её геометрически, найдя также .

б) Решить её симплекс-методом.

в) Сформулировать и решить симплекс-методом двойственную задачу.

2. Решить транспортную задачу методом потенциалов.

i \ j	1	2	3	4	ai
1	5	7	3	10	90
2	4	2	6	5	120
3	8	5	11	6	150
bj	140	110	70	40

Первоначальный план построить способом

минимального элемента.

3. «Игра с природой».

s=1; t=1; u=1; v=1.

s+5	t+6	u+7	v+8
t	v	s	u+20
u	t+15	v+15	s+15
u+15	s	v	t

Сформировать численную матрицу

и найти стратегии игрока, оптимальные

в смысле критериев Лапласа, Вальда,

Гурвица (при ) и математического

ожидания (при ).

4. Антагонистическая игра в случае непрерывной функции платежей.

Найти седловую точку и цену игры:

А)

В)

Значения параметров взять из задачи 3.

5. Матричная игра. Задана платёжная матрица. А= .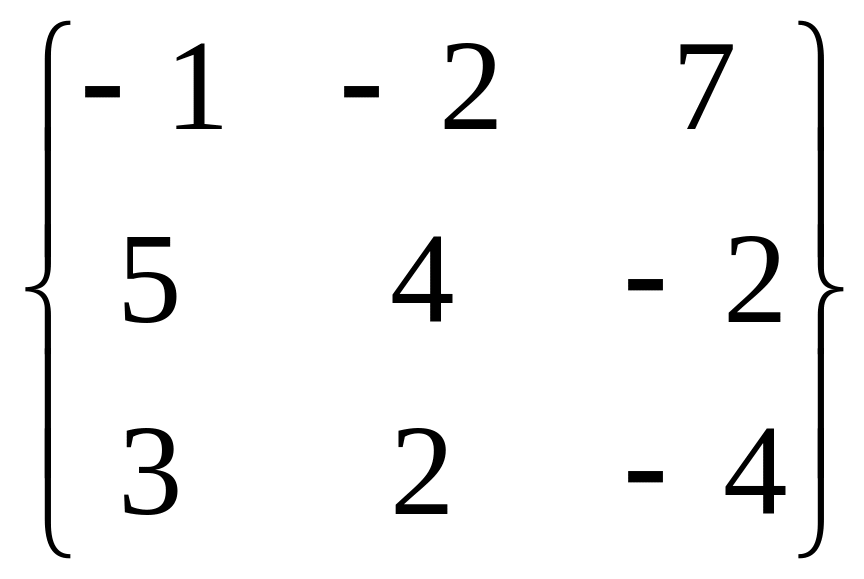

Проверить, существует ли седловая точка в игре. Если нет, найти оптимальные смешанные стратегии игроков.

6. Сетевое планирование.

а1	а2	а3	а4	а5	а6	а7	а8	а9	а10
-	-	а1	а2, а3	а2, а3	а4, а5	а4, а6	а6, а7	а7	а6, а7
5	10	5	15	15	10	20	10	15	5

Задана структурно-временная таблица.

Дать графическое представление структуры работ; построить временной сетевой график; найти критический путь и время выполнения всей работы; указать некритические дуги, некритические работы и резервы времени.

Вариант 2.

1. Дана задача линейного программирования:

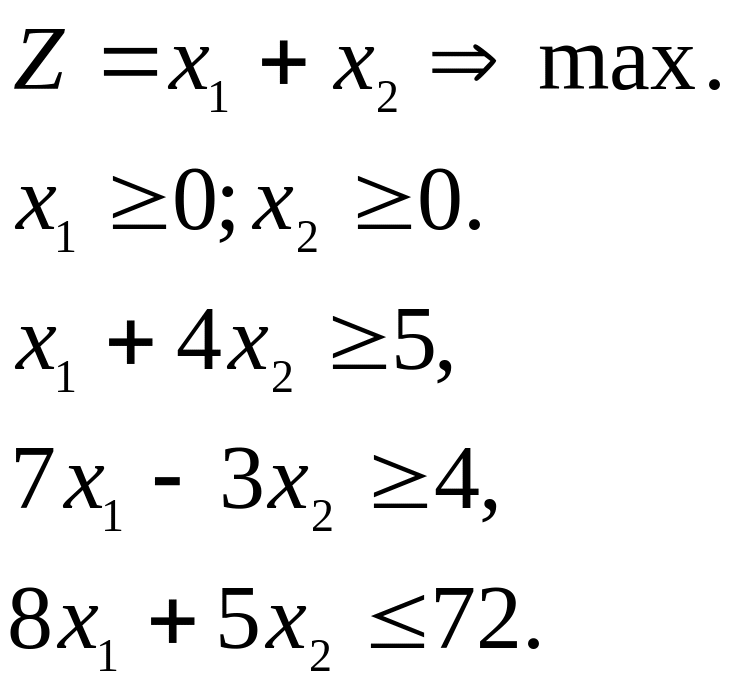
а) Решить её геометрически, найдя также .

б) Решить её симплекс-методом.

в) Сформулировать и решить симплекс-методом двойственную задачу.

2. Решить транспортную задачу методом потенциалов.

i \ j	1	2	3	4	ai
1	5	2	3	4	65
2	4	3	2	1	78
3	1	2	2	5	97
bj	40	60	80	60

Первоначальный план построить способом

северо-западного угла