
7.8 Расчет переходных процессов методом интеграла Дюамеля.
Пусть
входное воздействие задано функцией
![]() при
при
![]()

Полученное многоступенчатое воздействие математически выражается суммой
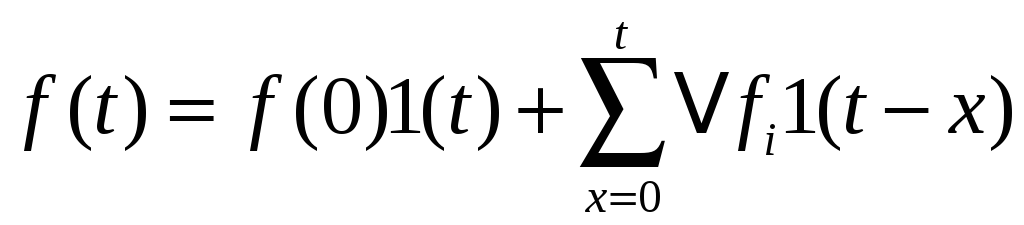
На основании принципа суперпозиции можно утверждать, что общая реакция цепи на ступенчатое воздействие равно сумма выходных сигналов, обусловленных действием каждого ступенчатого сигнала.
При
уменьшении
![]() интервалов до
бесконечно малых интервалов
интервалов до
бесконечно малых интервалов
![]() ступенчатая кривая воздействия перейдет
в заданную кривую
ступенчатая кривая воздействия перейдет
в заданную кривую
![]() ,
сумма заменится на интеграл,
,
сумма заменится на интеграл,
![]() на
на
![]()
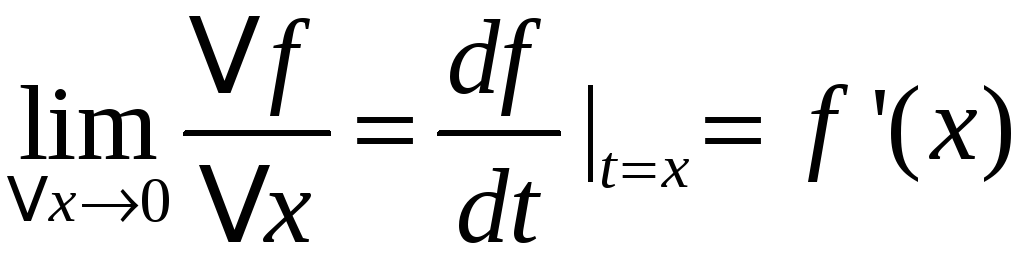
Окончательно
получим точное выражение для отклика
![]() ,
называемое интегралом Дюамеля или
суперпозиционным интегралом.
,
называемое интегралом Дюамеля или
суперпозиционным интегралом.

Где![]()
![]() - реакция цепи на начальный скачок
- реакция цепи на начальный скачок
![]() при
при
![]()
![]() переходная
характеристика
переходная
характеристика
![]() производная от
воздействия по времени в точке
производная от
воздействия по времени в точке
![]()
![]() переходная
характеристика, в которой вместо
переходная
характеристика, в которой вместо
![]() подставляют
подставляют
![]() .
.
ЗАМЕЧАНИЕ.
Если в полученном выражении под интегралом
функция зависит только от
![]()
то
ее можно вынести, т.к. при интегрировании
приращение происходит по
![]()
Общие правила расчета переходных процессов методом интеграла Дюамеля.
-
Для заданного отрезка выбирают наиболее простой вид формулы интеграла Дюамеля.
-
Любым методом определяют переходную функцию
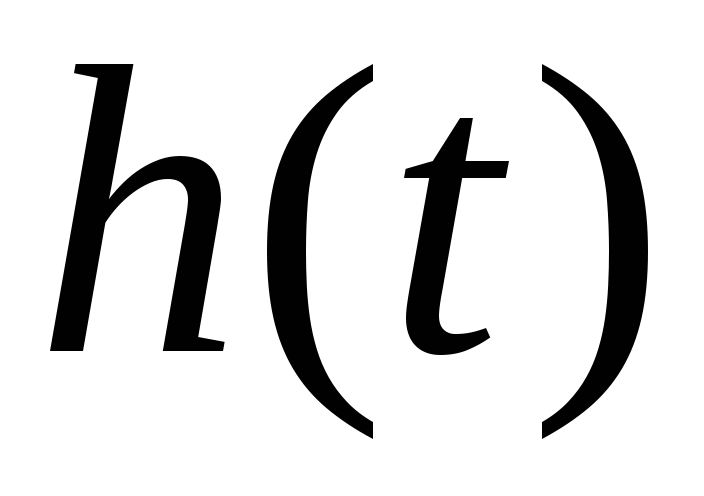 и по ней при необходимости -
и по ней при необходимости -
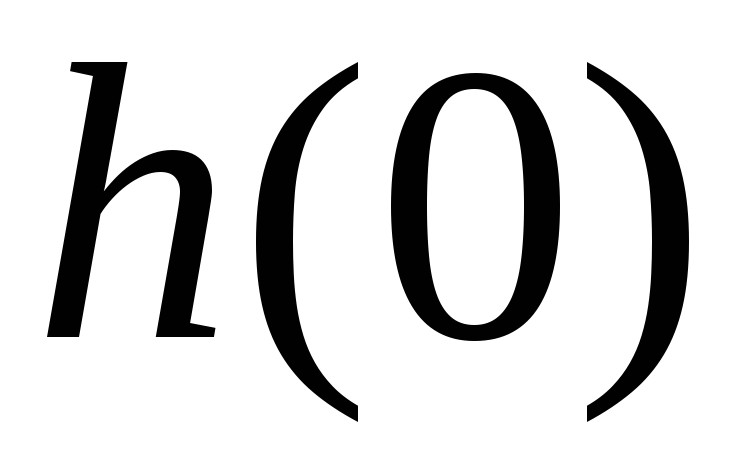 ,
,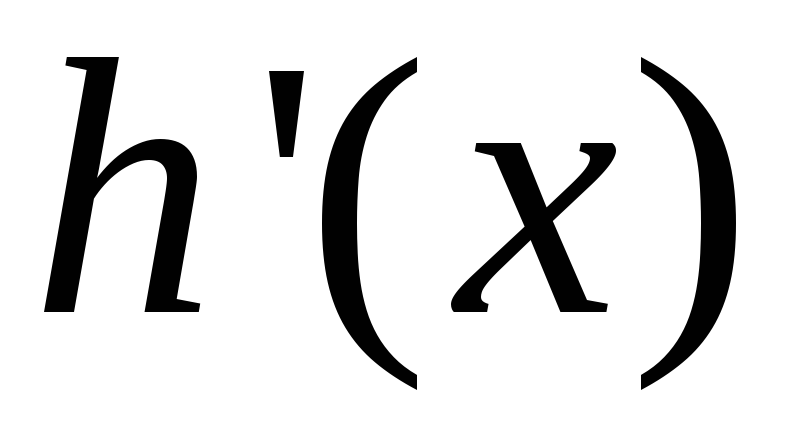 или
или
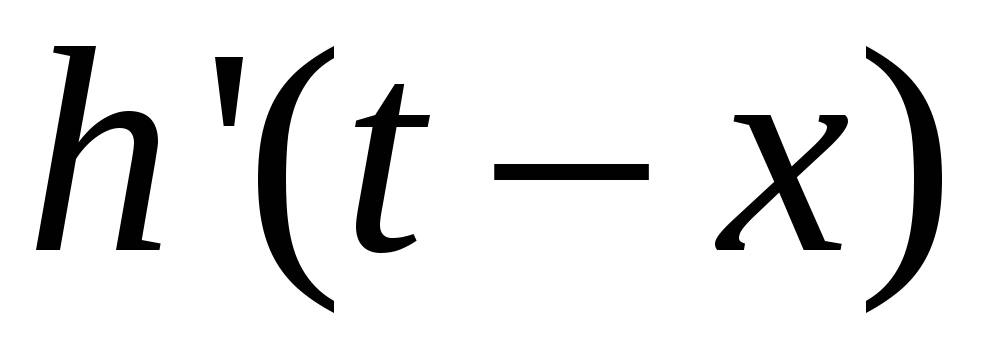
-
Находим при необходимости
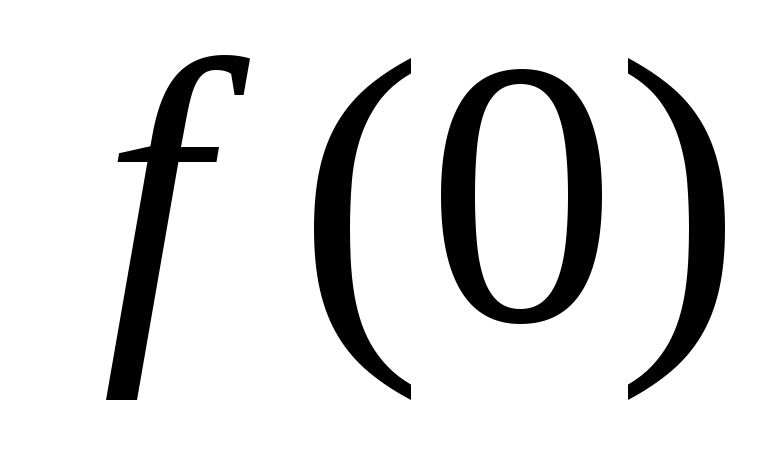 ,
,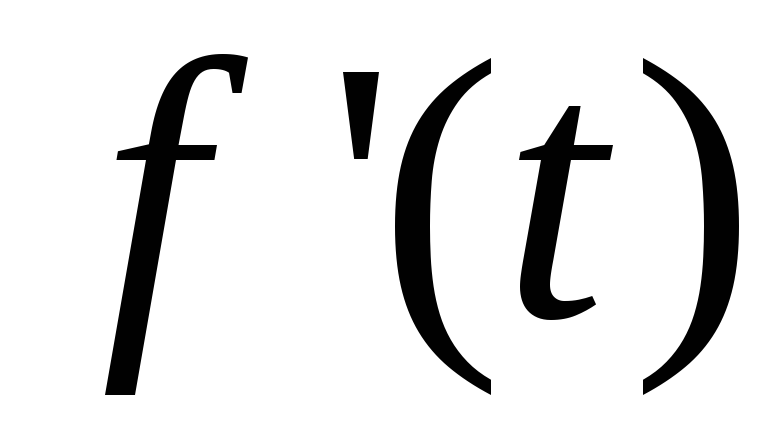 или
или
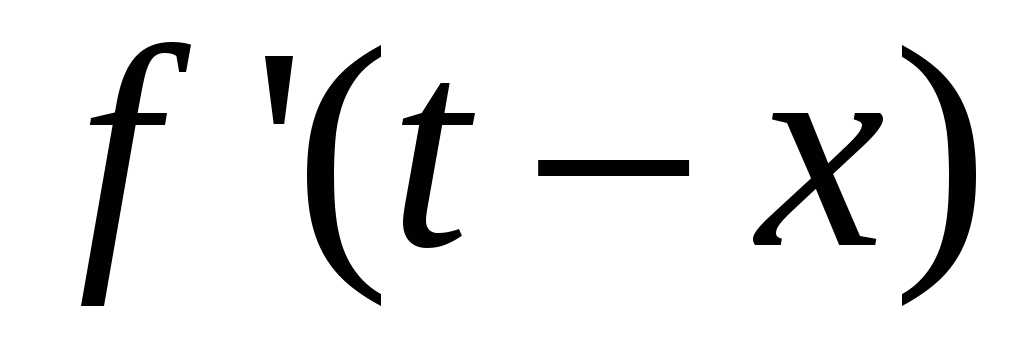
-
Полученные функции представляют в выбранную формулу интеграла Дюамеля.
-
Проводят графическое построение полученного отклика
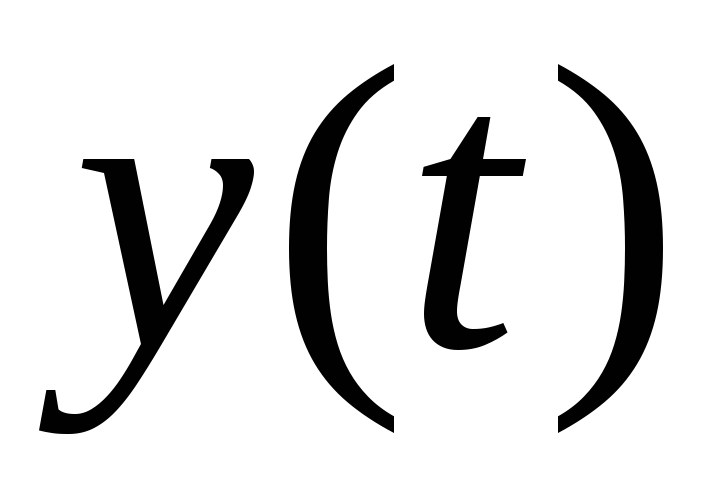
ВОПРОСЫ
-
Какой режим работы называется установившимся.
-
Какой режим работы называется переходным процессов (пример)
-
Законы коммутации (пример)
-
Какие цепи называются цепями “n” - порядка
-
Как связаны между собой
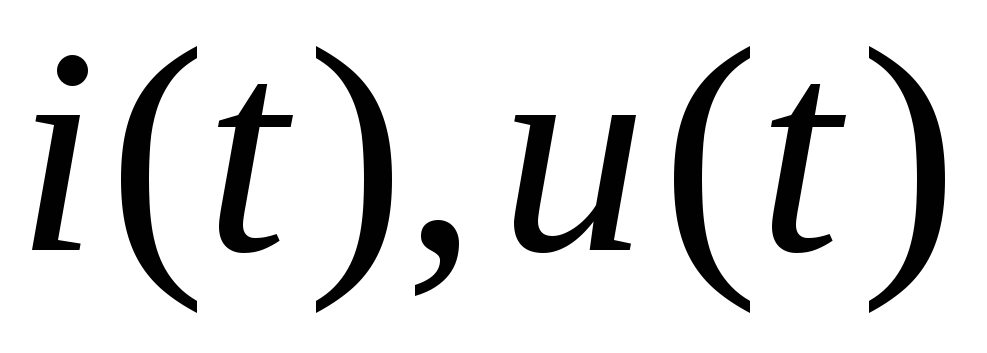 на
на
 и
и
 элементах цепи?
элементах цепи? -
Как рассчитать время установления ? (пример)
-
Какой процесс называется апериодичным, колебательным? (пример)
-
В чем сущность операторного метода расчета переходных процессов в цепи?
-
Единичная функция, каково ее операторное значение?
-
Закон Ома в операторной форме.
-
Законы Кирхгофа в операторной форме.
-
Связь комплексной передаточной функции и операторной.
-
Устойчивые и неустойчивые цепи (пример).
-
Критерий Гурвича (пример).
-
Единичная импульсная функция и ее свойства.
-
Интеграл Дюамеля.
Анализ частотного состава колебаний.
Если
несколько источников напряжения с
разными частотами
![]()
Амплитудами
![]() и начальными фазами
и начальными фазами
![]() присоединить последовательно
к
присоединить последовательно
к
![]() -цепи,
то напряжение и ток в этой цепи окажутся
несинусоидальными
-цепи,
то напряжение и ток в этой цепи окажутся
несинусоидальными
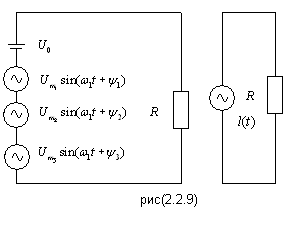
Можно считать, что на цепь воздействует только одна несинусоидальная
периодическая
ЭДС
![]() , которую можно представить в виде ряда
, которую можно представить в виде ряда
![]()
![]() постоянная
составляющая или нулевая гармоника
постоянная
составляющая или нулевая гармоника
![]() первая или основная
гармоника
первая или основная
гармоника
Остальные члены называются высшими гармониками
Где
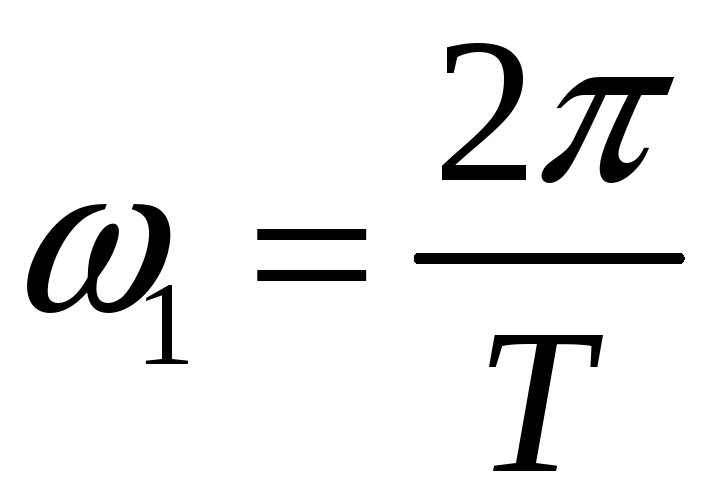 основная частота
основная частота
![]() период несинусоидального
периодического колебания
период несинусоидального
периодического колебания
![]() амплитуды гармоник
амплитуды гармоник
![]() начальные фазы
гармоник.
начальные фазы
гармоник.
Все сигналы, отличные от гармоничных, называются негармоническими.
На практике, чтобы получить напряжение негармонической формы, используют электронное устройство с операционным усилителем, называемое сумматором напряжений.
![]() на выходе сумматора
пропорционально сумме мгновенных
напряжений, подведенных к входам
сумматора.
на выходе сумматора
пропорционально сумме мгновенных
напряжений, подведенных к входам
сумматора.
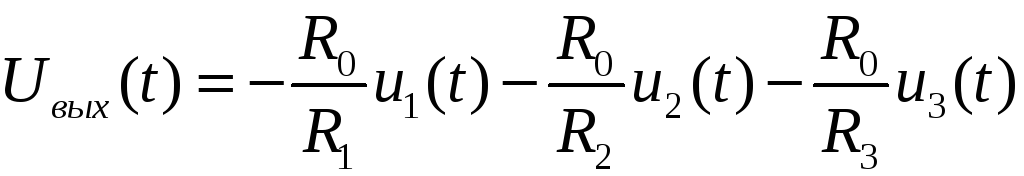
Если
![]() ,
то уравнение упрощается
,
то уравнение упрощается
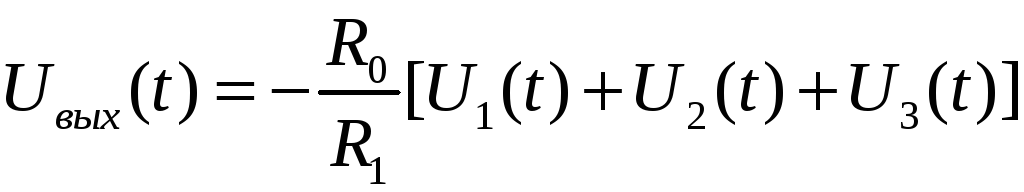
Ряд Фурье.
Всякая периодическая функция, удовлетворяющая условиям Дирихле, т.е. ограниченная, имеющая за полный период конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть разложена в виде тригонометрического ряда Фурье.
По
ортонормированной тригонометрической
системе ряд Фурье определяется для
каждой периодической функции![]() с
периодом
с
периодом
![]() ,
интегрируемой на отрезке
,
интегрируемой на отрезке
![]() Это ряд вида
Это ряд вида
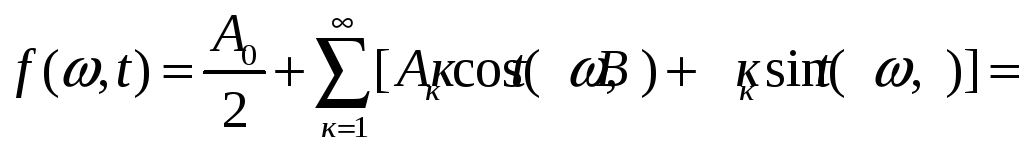
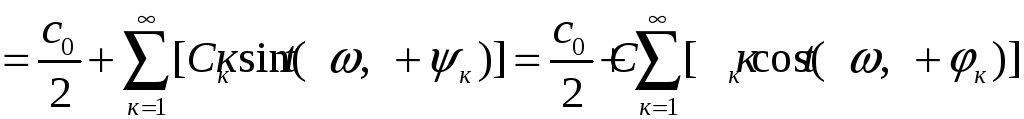
С коэффициентами Фурье, определенными по формуле Эйлере-Фурье.
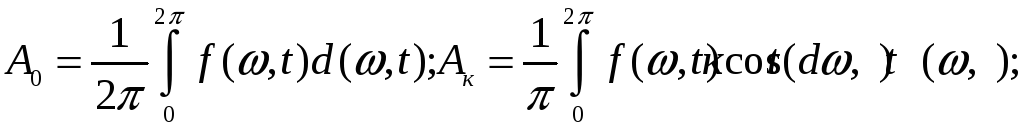
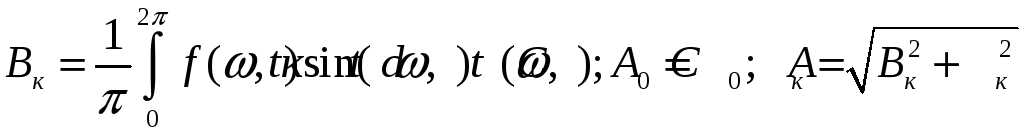

![]()

![]()
При
определении углов
![]() и
и
![]() надо учитывать
надо учитывать
![]() и
и
![]() ,т.е.
в какой четверти этот угол находится,
и обратный переход
,т.е.
в какой четверти этот угол находится,
и обратный переход
![]()
В точках разрыва ряд Фурье сходится

1.
Если функция
![]() четная, то она симметричная относительно
оси ординат.
четная, то она симметричная относительно
оси ординат.
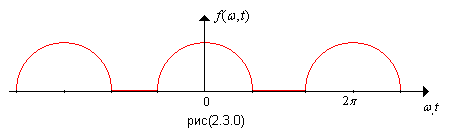
В этом случае отсутствуют синусоидальные составляющие.
![]() и
и

2.
Если функция
![]() нечетная, то она симметрична относительно
начала координат.
нечетная, то она симметрична относительно
начала координат.
В
этом случае отсутсвует постоянная
составляющая и косинусоидальная
составляющие
![]() и
и
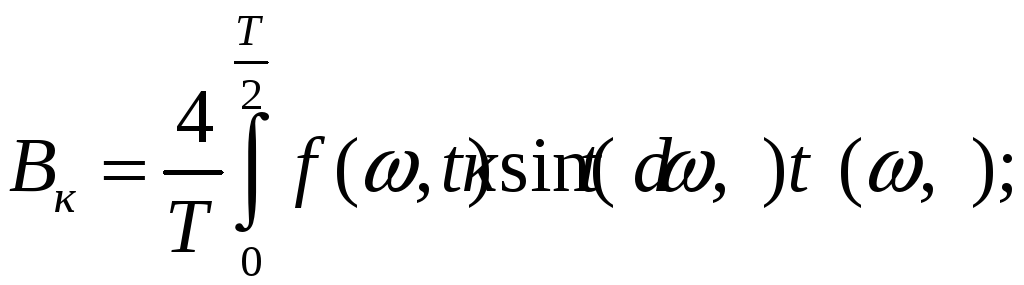
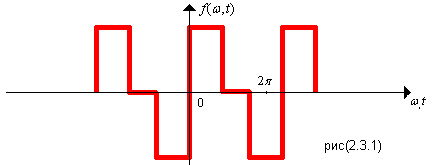
3.
Если функция симметричная относительно
оси абсцисс при совмещении двух
полупериодов
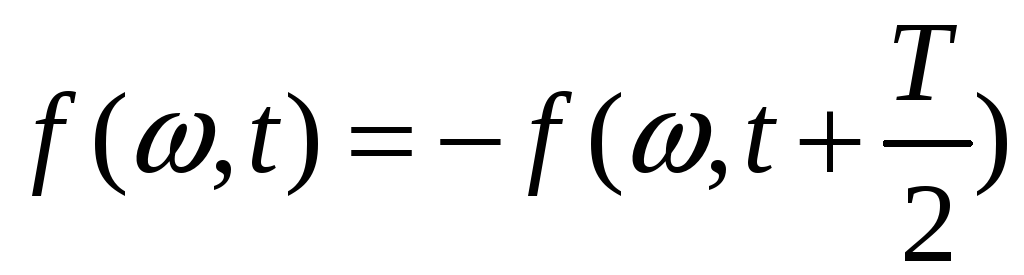 имеет
«зеркальное отражение полуволн
имеет
«зеркальное отражение полуволн
В
этом случае отсутствуют постоянная
составляющая и четные синусоидальные
и косинусоидальные составляющие
![]()
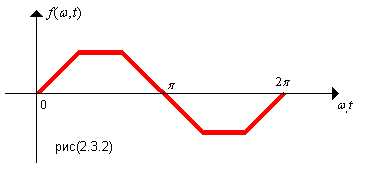
4.
Если функция симметрична относительно
оси ординат и оси абсцисс при совмещении
полупериодов
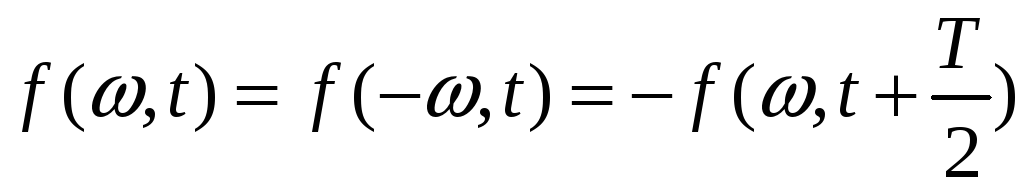
то
отсутствуют постоянная составляющая
и синусоидальные составляющие, а также
четные косинусоидальные составляющие
![]()
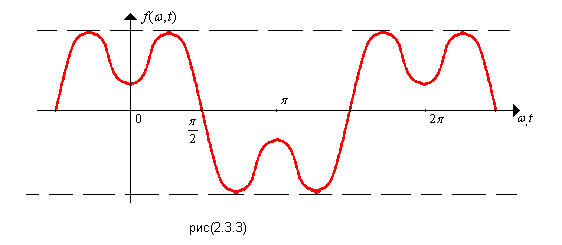 5.
Если функция симметрична относительно
начала координат и оси абсцисс при
совмещении полупериодов, то отсутствует
постоянная составляющая и все
косинусоидальные составляющие, а такде
синусоидальные составляющие
5.
Если функция симметрична относительно
начала координат и оси абсцисс при
совмещении полупериодов, то отсутствует
постоянная составляющая и все
косинусоидальные составляющие, а такде
синусоидальные составляющие
![]()

8.1. Интеграл Фурье
Если
![]() -
непериодическая функция, при которой
-
непериодическая функция, при которой
![]() ,
,
то двухсторонним преобразованием Фурье (спектральной плотностью) называется интеграл вида
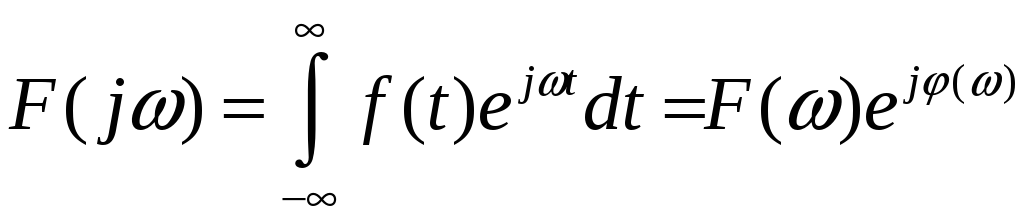
Где
![]() -
спектральная плотность
-
спектральная плотность
![]() амплитудно-частотная
характеристика
амплитудно-частотная
характеристика
![]() фазочастотная
характеристик
фазочастотная
характеристик
![]() время
время
Обратным преобразованием Фурье называется выражение
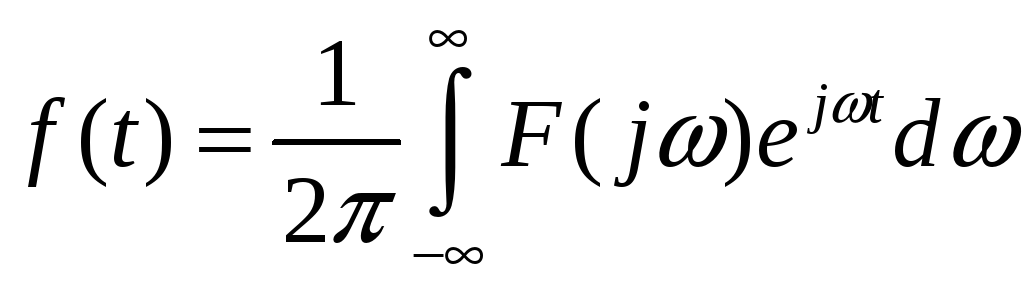
Заметим,
что преобразование Фурье является
частным случаем преобразования Лапласа
и получается из него при
![]() ,
т.е.
,
т.е.
![]()
Рассмотрим свойства преобразования Фурье.
ТЕОРЕМА ЗАПАЗДЫВАНИЯ
Если
функция
![]() соответствует спектральной плотности
соответствует спектральной плотности
![]() ,
то функция
,
то функция
![]() соответствует спектральной плотности
соответствует спектральной плотности
![]()
ТЕОРЕМА МАСШТАБИРОВАНИЯ
Если
функция
![]() соответствует спектральной плотности
соответствует спектральной плотности
![]() ,
то
,
то
Функция
![]() соответствует
спектральной плотности
соответствует
спектральной плотности
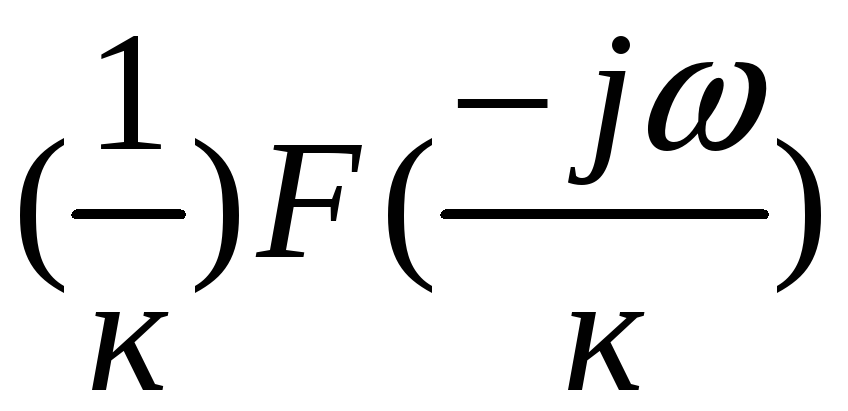
Где
![]() -
произвольная константа.
-
произвольная константа.
Заметим,
что дельта-функция
![]() может быть представлена интегралом
Фурье
может быть представлена интегралом
Фурье
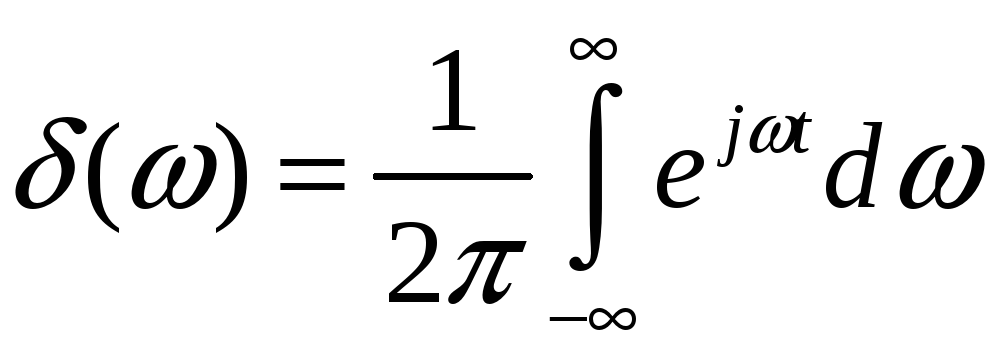
Или
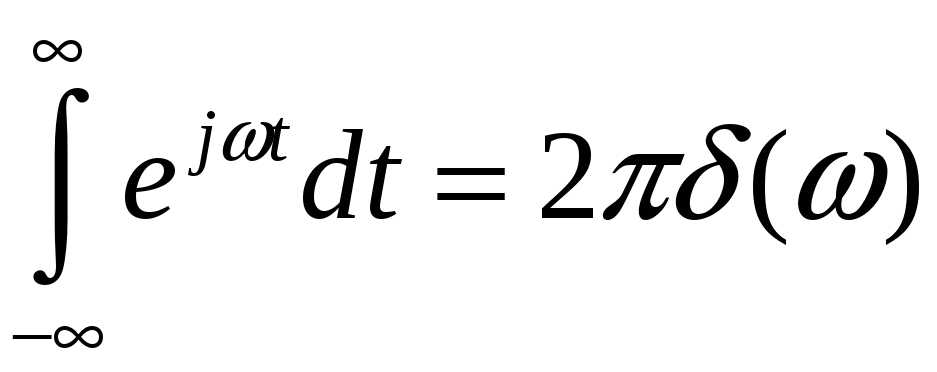
ФИЛЬТРУЮЩЕЕ СВОЙСТВО ДЕЛЬТА-ФУНКЦИИ
Пусть
![]() - любая непрерывная функция
- любая непрерывная функция
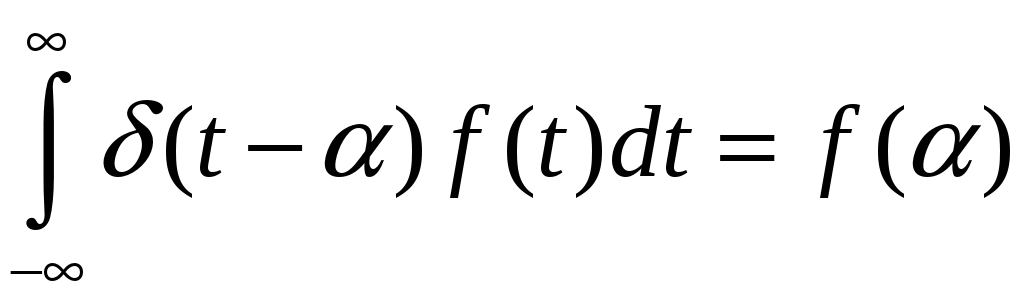
Где
![]() -
постоянная произвольная величина
-
постоянная произвольная величина
