5 Меоди розробки алгоритмів

5.1 Мета роботи – ознайомлення з різними методами розробки алгоритмів (динамічне програмування, жадібні алгоритми, розподіляй та володарюй, перебірні, перебірні з відсіканням) та їх особливостями. [1, c. 276-311; 3, с.383-482], порівняння застосовності методів складання алгоритмів для розв’язання різних завдань та часових характеристик отриманих алогритмів.

5.2 Методичні вказівки з організації самостійної роботи студентів

Найпростіший застосовуваний метод розробки алгоритму – це метод «декомпозиції». Цей метод інтуїтивний: якщо задача складна і її розв’язання не формулюється одразу, треба розбити задачу на підзадачі, використання розв’язання яких приведе до знаходження рішення. Цей метод лежить в основі поняття алгоритму, тому не потребує подальших коментарів та прикладів.

Метод «розподіляй та володарюй» пропонує розбивати задачу на менші підзадачі, кожна з яких розв’язується таким самим чином, як і вся задача в цілому, і тільки підзадача найменшого розміру може бути розв’язана тривіально без розподілення. Це підхід до розв’язання «зверху вниз». Очевидно, такі алгоритми частіше всього реалізуються як рекурсивні. Їх складання та наступне зрозуміння не становить труднощів. Зменшення задачі на кожному кроці досягається або зменшенням числа аргументів, від яких залежить задача, або пониженням їх значення. Такий прийом носить назву «зменшення розмірності задачі». Прикладом задачі, яку зручно розв’язувати таким чином є бінарний пошук елемента на відсортованому масиві. Якщо дано відсортований масив та треба сказати, чи є в ньому елемент a і на якій позиції, то ефективніше всього порівняти шуканий елемент з елементом на середині масиву. Якщо це і є він, то рішення знайдене, якщо ні, то одразу можна прийняти рішення, в лівій чи правій половині масиву треба шукати далі (якщо а менше серединного елемента, то він зліва, якщо більше, то справа). Умовно кажучи, тут задача була розділена на три: ліва половина, центральний елемент, права половина. Друга підзадача – тривіальна, на основі її рішення переходимо до розв’язання чи першої, чи третьої підзадач.

Метод «динамічного програмування». Не завжди використання «розподіляй та володарюй» є ефективним в чистому вигляді. Метод бінарного пошуку розділяв задачу на менші, які не перетиналися. Це щасливий випадок. Саме в таких випадках метод «розподіляй та володарюй» є ефективним. Але частіше всього під час розв’язання велика кількість підзадач, що отримують під час розподілення основної задачі на тому чи іншому кроці її розв’язання перетинаються. Це призводить до необхідності розв’язувати одну й ту саму задачу багато разів, що не є оптимальним. Прикладом може стати рішення задачі про числа Фібоначчі методом «розподіляй та володарюй». Числа Фібоначчі утворюють ряд, де F₀ = F₁= 1, F_i = F_i-1+F_i-2 для i >= 2. Неоптимальне розв’язання «в лоб» дає підхід: для знаходження, наприклад, F₈, треба знайти F₇

та F₆, для F₇ треба знайти F₆ та F₅, для F₆ – F₅ та F₄ , відповідно (рис. 5.1).

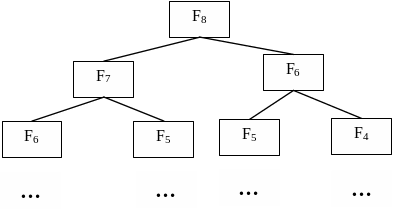
Рисунок 5.1 – Дерево обчислення підзадач Фібоначчі методом «розподіляй та володарюй»

Очевидно, що такий підхід в даному випадку не є оптимальний, краще просто підрахувати всі підзадачі, починаючи з 1-й й до тої, що потрібно, зберігаючи їх результат десь у масиві чи у примітивних змінних (для чисел Фібоначчі їх вистачить лише дві) та користуватися вже обчисленими значеннями підзадач, коли вони стануть потрібні. Так діє метод «динамічного програмування», який розв’язує задачу «знизу вверх». Для чисел Фібоначчі це означає знайти послідовно F₀ F₁ F₂ F₃ F₄ F₅ F₆ F₇ F₈.

У випадку чисел Фібоначчі всі підзадачі нам були потрібні, тому зайвих обчислень не було взагалі. Метод «динамічного програмування» розв’язує всі підзадачі з найпримітивніших до тої, що потребує розв’язання, не аналізуючи, чи знадобиться підзадача, чи ні. Це іноді призводить до зайвих кроків, але їх кількість значно менша, ніж у методі «розподіляй та володарюй».

Метод динамічного програмування часто використовують для розв’язання задач оптимізації, якщо можна довести, що оптимальне рішення на наступному кроці залежить від оптимальності усього попереднього шляху. Наприклад, задача знаходження мінімального за ціною шляху між усіма вершинами у зваженому графі розв’язується всім відомим алгоритмом Флойда [1, c. 187-191], який є типовим прикладом алгоритму «динамічного програмування».

Метод «жадібних» алгоритмів. Розглянемо задачу розміну суми грошей М у банкоматі з заданим набором доступних купюр. Найпростіше розв’язання задачі: видати найбільшою для даної суми купюрою більшу частину суми, потім наступною можливою найбільшою – частину залишку и т.д., доки залишок не зведеться до 0. Такий підхід названий «жадібним», тому що він за один крок намагається розв’язати більшу частину задачі. Типовим прикладом використання жадібного підходу є відомий алгоритм Дейкстри знаходження коротшого шляху між двома парами вершин [1, c.187-191]. Такий підхід дає оптимальне рішення тільки тоді, коли вдається довести, що «те, що добре локально, добре і глобально», але з усіх можливих алгоритмів для розв’язання задачі, він, очевидно, буде працювати за найменше можливе число кроків, тобто найшвидше.

У теорії алгоритмів відомий клас задач, оптимальне розв’язання яких можливе лише повним перебором. Такі задачі отримали назву NP-повних. Нажаль, перебірні алгоритми не застосовні на практиці, коли час отримання розв’язання важливий, тому жадібні алгоритми часто слугують допустимою «заміною» для розв’язання NP-повних задач. Способи наблизитися до оптимального рішення під час складання жадібних алгоритмів, які полягають у використанні всіляких перевірених практикою, але не завжди доказаних закономірностей, названі евристиками.

Дерева рішень[4, розділ 5.-7.]. Для написання інтелектуальних задач прийняття рішень частко застосовуються перебірні алгоритми на деревах рішень. Вузлом дерева рішення є поточна конфігурація рішення. Нащадками вузла є конфігурації, отримані з поточної допустимим застосуванням одного перетворення (одного з допустимих кроків, що покращують чи просто міняють конфігурацію). Наприклад, у шахах, таким кроком може стати один хід фігури. Очевидно, що корінь дерева – це дошка з початковою розстановкою фігур. Другий рівень дерева – це дошка з усіма можливими кроками першого гравця. Третій рівень – усі можливі відповіді супротивника на всі можливі перші кроки і т. ін. Дерева рішень у найпростішому випадку будують до ситуації, коли вже неможливо нічого змінити – це будуть листи дерева (для гри в шахи, це виграшна ситуація чи неможливість ходу). Потім дерево аналізують знизу вверх, присвоюють кожному вузлу дерева оцінку з точки зору корисності вершини для того, хто будував дерево. Якщо вершина – лист, то задача тривіальна, якщо ні, то оцінка залежить від оцінки нащадків: якщо хід того, хто будує, то обираємо максимальну з оцінок нащадків, якщо навпаки, то мінімальну. Це означає, що розглядаються потенційно однаково сильні гравці, кожен з яких з усіх можливих завжди обирає для себе найкращий хід. Такий підхід названий МІНІ-МАКСним. Потім, коли оцінена кожна вершина, у корені роблять висновок, який хід треба зробити, щоб отримати найкращий результат незалежно від наступних оптимальних ходів супротивника.

Приклад обрання ходу комп’ютера у грі «хрестики-нулики» на основі дерева рішень наведено у [1, c.291-296].

Вочевидь, розмір дерев рішень колосально великий та не застосовний на практиці, тому розробляються прийоми його скорочення: перебирати всього декілька рівнів в глибину, аналізувати не всі можливі кроки та ін. І в першому і в другому випадку може постраждати «інтелектуальність» програми.

Скорочення глибини перебору призводить до необхідності присвоювати оцінку неповній ситуації, наприклад, для «хрестиків-ноликів» ніхто не виграв та нема нічиєї. Як це можливо зробити? Треба знайти якісь непрямі ознаки, за якими можливо з великою долею впевненості сказати, чи може ситуація привести до виграшу, програшу або нічиєї. Для хрестиків-ноликів це кількість ходів, що залишилися до виграшу, кількість можливих наступних виграшних альтернатив з даної конфігурації.

Відтинання кроків, аналіз яких не вплине на результат. Це здається неможливим, але існує спосіб аналізувати не всі гілки дерева рішень. На рис. 5.2 приведений фрагмент гіпотетичного дерева в процесі його побудови в глибину та паралельного аналізу вузлів. Будуємо вузли А-В-С. Оцінка листа С, а тому й попередня оцінка В – 3. Оцінюємо D у 12. E у 8. B = min(C,D,E) = 3. Будуємо F та G. Оцінка G = 2, тоді можна зробити висновок, що F<= 2 незалежно від оцінок інших нащадків F. A = max(B,F,H). Тому побудова та аналіз нащадків F вже ніяк не вплине на оцінку A. Нажаль, такого висновку не вдається досягнути під час аналізу третьої гілки: I = 14, попередня оцінка H = I = 14, 14 > 3, тому відкинути не вдається; J = 5, H = min(H,J) = 5, 5> 3; K = 2, H = min(H, K)=2. A = max(B,F,H) = 3.

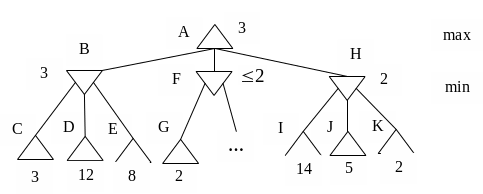
Рисунок 5.2 – Альфа-бета відсікання

З прикладу ясно видно, що ефективність альфа-бета відтинання залежить від порядку аналізу вершин.

5.3 Варіанти індивідуальних завдань

1. Реалізувати гру хрестики-нулики людини з комп'ютером. Комп'ютер ухвалює рішення щодо ходу на підставі аналізу дерева рішень з відсіканням (у якості методу відсікання можна обрати альфа-бета відсікання). [1. c.291 - 301, 4. розділ 5.-7.]

2. Реалізувати пошук шляху в лабіринті між двома кімнатами на підставі алгоритму пошуку з поверненням та пошуку навширшки (волновий алгоритм). Лабіринт задається неорієнтованим графом кімнат, з’єднаних дверима.  [1. с. 208 – 220, 4. с. 109-136, 153-173]

3. Реалізувати програму підбора оптимального маршруту за часом, витраченим на шляху між двома станціями метро (алгоритм Дейкстри або Флойда). Схема метрополітену задана зваженим орієнтованим графом. Для кожного прольоту між станціями відомий час проходу поїзда (вага дуги). [1 c. 183-195]

4. Реалізувати завдання пошуку оптимального маршруту листоноші при розносі пошти (задача комівояжера) жадібним алгоритмом. Схема розташування поштових скриньок задається зваженим неорієнтованим повним графом, де вага ребра відповідає відстані між поштовими скриньками по дорозі. [1 с. 288-291]

5. Реалізувати завдання пошуку оптимального маршруту листоноші при розносі пошти (задача комівояжера) методом локального пошуку. Схема розташування поштових скриньок задається зваженим неорієнтованим повним графом, де вага ребра відповідає відстані між поштовими скриньками по дорозі. [1 с. 303-306]

6. Реалізувати розв’язання задачі тріангуляції методом динамічного програмування [1 c. 283-288].

7. Реалізувати розв’язання задачі визначення оптимального порядку отримання добутку декількох матриць методом динамічного програмування так, щоб загальна кількість операцій була мінімальна [3, 395-404].

8. Реалізувати алгоритм визначення оптимального набору режимів роботи світлофора на перехресті (методи розв’язання задачі пофарбування вершин графа – жадібний) [1, c.15-22].

9. Задане прямокутне поле, поділене на клітини, Задача гравця пройти по такому полю з клітини-джерела до клітини-призначення. Потрапляння у кожну клітину поля надає гравцю бонус або штраф відомої величини. Запропонуйте алгоритм пошуку оптимального (за отриманими за прохід балами) шляху між двома клітинами поля [1, c.280-288, 3, с. 386-440].

5.4 Контрольні запитання та завдання

1. За якими параметрами можливо оцінити алгоритм?

2. Як обчислюється часова складність алгоритму?

3. Що таке клас NP-повних задач? Наведіть приклади таких задач.

4. Назвіть метод складання алгоритмів який дає найоптимальніше за часом але не завжди оптимальне за вимогами задачі розв’язання.

5. Коли варто застосовувати жадібні алгоритми?

6. Коли варто застосовувати алгоритми на основі динамічного програмування?

7. Коли варто застосовувати алгоритми типу «розділяй та володарюй»?

8. Які існують стратегії оптимізації алгоритмів повного перебору?

ПЕРЕЛІК ПОСИЛАНЬ

1. Ахо А., Хопкрофт Д., Ульман Д. Структури даних й алгоритми. М: Видавничий будинок «Вільямс», 2003.-384 с.

2. Карпов Ю.Г. Теория и технология программирования. Основы построения трансляторов. – СПб.:БХВ-Петербург, 2005. – 272 с.

3. Кормен Т., Лейзерсон Ч. , Ривест Р. Алгоритмы: построение и анализ - 2-е изд. - М. : БИНОМ. Лаб. знаний : Изд-во МЦНМО, 2004. - 955с.

4. Стюарт Рассел, Питер Норвиг Искусственный интеллект: современный подход(AIMA) - 2-е узд.: Пер. с англ. - М.:Издательский дом «Вильямс», 2005. – 1424 с.

5. Кнут Д. Мистецтво програмування. Том 1,2,3. – М.: Видавничий будинок «Вільямс», 2001. – 720 с.

Навчальне видання

МЕТОДИЧНІ ВКАЗІВКИ

до лабораторних робіт з дисципліни

"СТРУКТУРИ ДАНИХ ТА АЛГОРИТМИ"

для студентів напрямку 7.080202 – «Прикладна математика»

Упорядники: ГАЛУЗА Олексій Анатолійович

ЛЕЩИНСЬКА Олена Леонідівна

Відповідальний випусковий З.В. Дудар

Редактор

Комп’ютерна верстка

План 2007, поз.

Пiдп. до друку Формат 60x84 _1/16. Спосіб друку – ризографія.

Умов.друк.арк. Облiк. вид.арк. Тираж прим.

Зам. № Цiна договiрна.

ХНУРЕ, 61166 Харкiв, просп. Ленiна, 14.

Віддруковано в навчально-науковому

видавничо-поліграфічному центрі ХНУРЕ