Лінійні алгоритми

Всі алгоритми сортування, які були розглянуті раніше, універсальні й не накладають ніяких обмежень на множину елементів, що належить впорядкувати. Основою роботи таких алгоритмів є порівняння елементів, що впорядковують, між собою. У той час, якщо ми маємо яку-небудь апріорну інформацію про вхідні дані (а на практиці найчастіше саме так і буває), то цю інформацію треба використати. Це дає можливість будувати алгоритми, що працюють істотно швидше, навіть за час O(n), тобто є лінійними.

Перший з таких алгоритмів ‑ сортування підрахунком. Допустимо, нам відомо, що елементи вихідного масиву X(n) ‑

цілі числа у відомому діапазоні: x_i  A, де A={a| a Z, l a u } (l,u  Z заздалегідь відомі). Крім того, припустимо, що k=dim A n.

Алгоритм легко модифікується під дані з будь-якої кінцевої підмножини цілих чисел, причому множина A навіть необов'язково повинна містити всі цілі числа з інтервалу [l,u]. Для простоти припустимо, що A ‑ множина всіх цілих позитивних чисел не перевищуючих деякого відомого k.

Ідея сортування підрахунком полягає в тому, що нам зовсім немає необхідності переставляти елементи, як ми це робили раніше. Досить підрахувати скільки разів кожен елемент множини A зустрічається у вхідному масиві, після чого заповнити цей (або інший) масив заново потрібною кількістю елементів з A. Для цього потрібно створити додатковий масив C(k), у якому c_i ‑ кількість входжень числа i у масив X. Запишемо цей алгоритм метамовою.

Proc CountSort

C = 0

for i = 1 to n do C_xi = C_xi+1

j = 1

for i = 1 to k do

while C_i > 0 do

x_j = i

j = j + 1

C_i = C_i - 1

endwhile

endfor

End CountSort

Незалежно від розміру масив X проглядається тільки двічі: один раз при підрахунку, другий ‑ при заповненні. Складність операції обнуління масиву C(k) (C = 0) дорівнює O(k) і не вплине на порядок складності алгоритму в цілому, а при k<<n взагалі позначиться мало. Складність алгоритму дорівнює O(n+n+k) = O(n), тобто лінійна, причому в кожному разі.

Недоліки цього алгоритму наступні. По-перше, необхідність виділення додаткового масиву. По-друге, цей алгоритм неможливо застосувати, коли в масиві разом із числами записані додаткові дані. Така ситуація характерна, наприклад, при сортуванні записів.

Якщо з першим недоліком нічого не поробиш, то із другим цілком можна впоратися. Для цього скористаємося ідеєю, що лежить в основі сортування перерахуванням (алг. EnumSort).

Для кожного числа x_i підрахуємо скільки у вхідній послідовності елементів, менших цього числа, тобто, фактично, його позицію в результуючому масиві, після чого не просто заповнимо масив R потрібними числами, а перенесемо їх з масиву X. Запишемо модифікований алгоритм сортування підрахунком і розглянемо докладніше його роботу.

Proc ModifiedCountSort

C = 0

for i = 1 to n do C_Xi = C_Xi+1

for i = 2 to k do C_i = C_i + C_i-1

for i= n downto 1 do

r_Cxi = x_i

C_Xi = C_Xi - 1

endfor

End ModifiedCountSort

Пояснення. Після ініціалізації спочатку поміщаємо в C_i кількість елементів масиву X, рівних i. Потім знаходимо часткові суми C_i = C_i + C_i-1 (i=2..k) ‑ кількості елементів, що не перевершують i. Нарешті, кожен з елементів масиву X переміщається на потрібне місце в масиві R. Справді, якщо всі n елементів різні, то у відсортованому масиві число x_i повинне стояти на місці з номером C_Xi, оскільки саме стільки елементів масиву X не перевершують x_j. Якщо в масиві X зустрічаються повторення, то після кожного запису числа x_i у масив R число C_Xi зменшується на одиницю, так що при наступній зустрічі із числом, рівним x_i, воно буде записано на одну позицію лівіше. Оскільки в порівнянні з алгоритмом сортування підрахунком, у його модифікації ModifiedCountSort додався тільки один цикл перегляду масиву C(k), то складність алгоритму залишилася лінійною.

Алгоритм ModifiedCountSort має важливу властивість – стійкість. Вона означає, що якщо у вхідному масиві присутні кілька рівних чисел, то у вихідному масиві вони будуть стояти в тому ж порядку. Це має сенс при роботі із записами з полями, наприклад, x й t, де x ‑ числа, за якими ми сортуємо, а t ‑ довільні об'єкти, і хочемо залишити порядок розташування елементів з однаковими x тим же.

Властивість стійкості відіграє вирішальну роль у методі, який називається цифровим сортуванням. Нехай, наприклад, потрібно відсортувати послідовність дат. Це можна зробити за допомогою будь-якого алгоритму сортування, порівнюючи дати в такий спосіб: зрівняти роки, якщо роки збігаються ‑ зрівняти місяці, якщо збіглися й місяці ‑ зрівняти числа. Замість цього можна просто тричі відсортувати масив дат за допомогою стійкого алгоритму: спочатку по днях, потім по місяцях й, нарешті, по роках. Стійкість дає нам гарантію, що після сортування по роках не порушиться порядок проходження днів і місяців. Зверніть увагу, що спочатку потрібно сортувати по днях, тобто по «молодшій» ознаці.

Цифрове сортування використовується не тільки для сортування даних за декількома ознаками, але й для цілих чисел. У цьому випадку ми припускаємо, що кожен елемент масиву X(n) складається з d цифр, причому цифра номер 1 ‑ молодший розряд, а цифра номер d ‑ старший (така інтерпретація й дала назву методу). Тоді, якщо як ознаки використовувати цифри у відповідних розрядах елементів масиву, то одержимо

Proc RadixSort(X(n),d)

for i = 1 to d do

відсортувати стійким алгоритмом масив X по i-ої цифрі

endfor

End RadixSort

Складність цифрового сортування залежить від складності обраного стійкого алгоритму. Якщо цифри приймають значення від 0 до k-1, де k не занадто велике, то очевидно найкращий алгоритм ‑ модифіковане сортування підрахунком ModifiedCountSort.

Для n d-розрядних чисел кожен прохід займає ((n+k), а оскільки робиться d проходів загальний час роботи ((dn+kd). Якщо d = const й k = O(n), то цифрове сортування працює за лінійний час.

Нехай тепер необхідно відсортувати масив X(n) записів (не можна використати сортування підрахунком) по деякому ключу key (key ‑ елемент запису). Припустимо, що значення ключа лежать у діапазоні 1 … n і не повторюються (наприклад, номера телефонів). Тоді можна організувати сортування X у такий спосіб:

Proc PreBinSort

for i = 1 to n do r_x[i].key = x_i

End PreBinSort

Цей алгоритм обчислює, де в масиві R повинен перебувати елемент x_i і поміщає його туди. Очевидно, цей алгоритм лінійний.

Для тих же обмежень на вихідні дані можна побудувати лінійний алгоритм, що не використовує другого масиву R. По черзі переглянемо всі елементи x_i … x_n... Якщо j = x_i.key ≠i, то міняємо місцями записи в чарунках x_i й x_j. Якщо після перестановки новий запис в x_i має ключ k≠i, то міняємо місцями x_i й x_k і т.д. Кожна перестановка ставить хоча б один запис у потрібному порядку, тому даний алгоритм має час виконання (n). Цей алгоритм наведений нижче.

Proc PreBinSortSimple

for i = 1 to n do

while x_i.key ≠ i do x_i x _x[i].key

endfor

End PreBinSortSimple

Розширенням алгоритму PreBinSort на випадок, коли значення елементів можуть повторюватися, є, так називана «кишенькове сортування». В алгоритмі PreBinSort ми завели додатковий масив R, у який записували елементи масиву X, використовуючи як індекси x_i.key. Очевидно, якщо цей алгоритм використати для елементів з однаковими значеннями поля key, то наступний буде затирати попередній й інформація втратиться. Пропонується для кожного можливого значення key = i використати не одну допоміжну чарунку r_i («кишеню»), як в алгоритмі PreBinSort, а багато (в ідеалі ‑ стільки, скільки потрібно).

Тоді допоміжний масив R(n) повинен містити не значення, а покажчики на початки динамічних списків. У кожний із цих списків ми будемо складати записи з рівним ключем. Після того, як всі записи вихідного масиву розкидані по списках («кишенях»), залишається тільки об'єднати всі ці списки в один. Втім, алгоритм набагато простіше зрозуміти, якщо уважно подивитися на рис. 3.6.

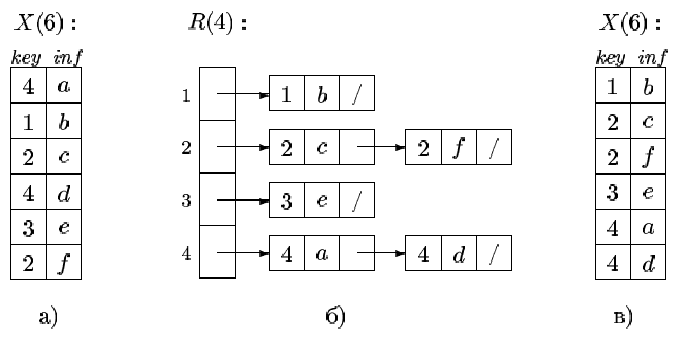
Рисунок 3.6 ‑ Кишенькове сортування: (a)даний масив , (б) масив у «кишенях», (в) упорядкований масив. Тут inf ‑ інформаційне поле запису x_i (у загальному випадку воно може бути не одне).

Алгоритм BinSort реалізує кишенькове сортування. У ньому використовуються операції додавання елементів у список і злиття двох списків. Можна не поєднувати списки в один, а переписати їхній вміст у вихідний масив у потрібному порядку, як показано на рис.3.6. Очевидно, кишенькове сортування лінійне.

Proc BinSort

for i = 1 to n do

Rx_i.key x_i

endfor

for i = 2 to n do

Merge(r₁, r_i)

endfor

End BinSort

Ідея більшості перерахованих лінійних алгоритмів ‑ використання значень елементів як індексів, а не порівняння елементів між собою. Це можливо при виконанні певних обмежень на значення елементів. Такий підхід годиться тільки для випадку сортування цілих чисел. Для чисел з плаваючою крапкою також можливо побудувати лінійний алгоритм, але обмеження будуть жорсткішими.

Розглянемо модифікацію кишенькового сортування для чисел з плаваючою крапкою у діапазоні [0,1), що називають «сортуванням вичерпуванням». Ідея алгоритму в тім, що проміжок [0,1) ділиться на n рівних інтервалів, і числа з i-го інтервалу складаються в i-у «кишеню», причому номер i-ї кишені дорівнює нижній границі i-го інтервалу. Номер інтервалу, якому належить x_i, легко обчислюється, як ціла частина від добутку x_i на n, тобто, дорівнює nx_i. Зверніть увагу, що кишені при цьому нумеруються від 0 до n-1. Потім кожна з «кишень» сортується окремо (будь-яким нелінійним методом), і всі вони зливаються в одну. Таким чином, відмінність від кишенькового сортування полягає в тому, що номери кишень (тобто, додаткового списку) відповідають не значенням сортуємих елементів, а номерам інтервалів, яким вони належать. Цей метод реалізований у вигляді алгоритму BucketSort, а приклад його роботи наведений на рис. 3.7.

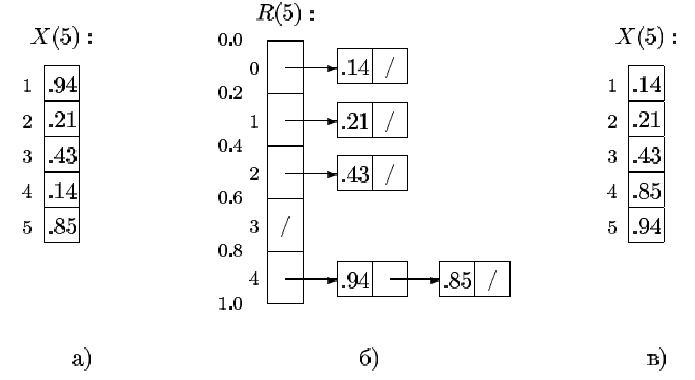
Рисунок 3.7 ‑ Сортування вичерпуванням: (a) вихідний масив, (б) «кишені», (в) упорядкований масив. Нуль перед десятковою крапкою пропущений з естетичних міркувань.

Proc BucketSort

for i = 1 to n do

r  x_i

endfor

for i = 1 to n do

сортування i-ї кишені

endfor

for i = 2 to n do

Merge(r₁, r_i)

endfor

End BucketSort

Вибір кількості карманів n залежить від кількості вихідних даних. Робимо багато кишень –. можливо, більшість із них буде порожніми, тобто ми даремно витрачаємо пам'ять. Робимо мало ‑ в кожній кишені може виявитися список такої довжини, що вартість його упорядкування перекреслює всі переваги кишенькового сортування. Як правило, розумно робити кількість інтервалів рівним розміру вихідного масиву.

Якщо припустити, що в середньому на кожен інтервал потрапить по одному числу, то внутрішнє сортування кишені не буде потрібно. Очевидно, якщо ця умова не виконається, то час роботи буде визначатися тим алгоритмом, що ми виберемо для упорядкування кишень.

Помітимо також, що якщо числа належать інтервалу [a..b), то при розподілі чисел по кишенях їх потрібно привести до інтервалу [0..1). Тобто номер кишені буде обчислюватися як .

3.3 Варіанти завдань

Реалізувати алгоритми сортування відповідно до варіанта з підрахунком кількості необхідних для сортування кроків. Оцінити ефективність (часову складність) алгоритмів на однакових наборах даних. Розглянути такі набори: уже впорядкований, впорядкований у зворотному порядку, довільний.

1. квадратичні: вставками; логарифмічні: пірамідальна; лінійні: підрахунком;

2. квадратичні: пухирцем; логарифмічні: швидка; лінійні: кишенькова;

3. квадратичні: перерахуванням; логарифмічні: злиттям; лінійні: вичерпуванням;

3.4. Контрольні запитання та завдання

1. По яких параметрах можна оцінювати алгоритм?

2. Як обчислюється часова складність алгоритму?

3. Алгоритми сортування з якими часовими складностями Вам відомі?

4. Які алгоритми сортування називаються стійкими?