3 Алгоритми сортування послідовностей

3.1 Мета роботи – ознайомлення з різними алгоритмами сортування послідовностей і порівняння їхніх тимчасових характеристик.

3.2 Методичні вказівки з організації самостійної роботи студентів

Сортування ‑ це завдання розташування довільних об'єктів у порядку (не-) убування або (не-)зростання деякої ознаки. Існує велика кількість методів сортування, які відрізняються друг від друга як тимчасовою складністю, так й універсальністю [5, том 3, c.5-247]. У даній роботі розглядаються типові алгоритми квадратичної, логарифмічної й лінійної складностей.

Квадратичні алгоритми

Нехай потрібно впорядкувати масив за неубуванням, для чого пропонується використати наступний підхід: для , кожен елемент будемо вставляти в потрібне місце серед упорядкованих раніше елементів , розсовуючи їх за рахунок видалення . Запишемо цей алгоритм на метамові.

Proc InsertSort

for i = 2 to n

t = x_i

j = i - 1

while (j > 0) and (x_j > t) do

x_j+1 = x_j

j = j - 1

endwhile

x_j+1 = t

endfor

End InsertSort

Цей метод, що називається «сортування вставками», у явному виді рідко використовується на практиці, однак покладена в його основу ідея добре працює, коли потрібно вставити новий елемент у вже впорядкований масив.

Ще одним елементарним методом сортування є так званий метод пухирця. Ідея методу полягає в упорядкуванні всіх пар сусідніх елементів. Масив проглядається зліва направо й, якщо x_i > x_i+1 (i=1…n-1), то вони міняються місцями. При цьому i-ий елемент (крім перш й останнього) бере участь у двох порівняннях, а це значить, що максимальний елемент масиву буде переміщатися («спливати») до правого кінця масиву й до кінця проходу виявиться останнім. За наступний прохід «спливе» другий за величиною елемент і т.ін., поки всі елементи не займуть свої місця. Очевидно, для цього буде потрібно не більше n-1 проходів. Оформимо тепер ці думки у вигляді алгоритму.

Proc Bubble

for i = 1 to n-1 do

for j = 1 to n-i do

if x_j > x_j+1 then x_j+1 ↔ x_j

End Bubble

Розглянемо ще одні метод, який можна віднести до розряду очевидних. Це метод сортування перерахуванням. Ідея методу проста. Для кожного елемента масиву X(n) підрахувати, скільки елементів менше його, тобто фактично знайти його положення в упорядкованому масиві. Для зберігання цієї інформації можна використати масив лічильників C(n). Тоді значення c_i+1 визначає положення елемента x_i у результуючому відсортованому масиві R(n).

Proc EnumSort

C = 0

for i = n downto 2 do

for j = i-1 downto 1 do

if x_i > x_j then C_i = C_i + 1

else C_j = C_j + 1

endfor

endfor

for i = 1 to n do r_Ci+1 = x_i

End EnumSort

Логарифмічні алгоритми

У раніше розглянутих методах сортування складності O(n²) при виборі найбільшого (найменшого) елемента губилася інформація про інші елементи, хоча перевірка й виконувалася. Існують алгоритми, що дозволяють зберігати проміжні результати процесу сортування й використовувати їх надалі для зменшення числа операцій, тобто часу роботи алгоритму. Розглянемо метод, що використовує пірамідально впорядковане двійкове дерево, представлене на суміжній пам'яті, тобто в одномірному масиві. Тому цей метод називають пірамідальним сортуванням.

Дерево називається пірамідально впорядкованим, якщо значення в кожній вершині не менше, ніж значення в кожній з її дочірніх вершин (якщо вони є).

Купою називається пірамідально впорядковане двійкове дерево, представлене, наприклад, в одномірному масиві A(n). У такому дереві для кожної вершини i повинне виконуватися властивість упорядкованості:

(3.1)

Це означає, що найбільший елемент дерева (або будь-якого піддерева) перебуває в кореневій вершині дерева (цього піддерева).

Двійкове дерево називається частково впорядкованим, якщо властивість (3.1) виконується для кожної його вершини, крім кореня.

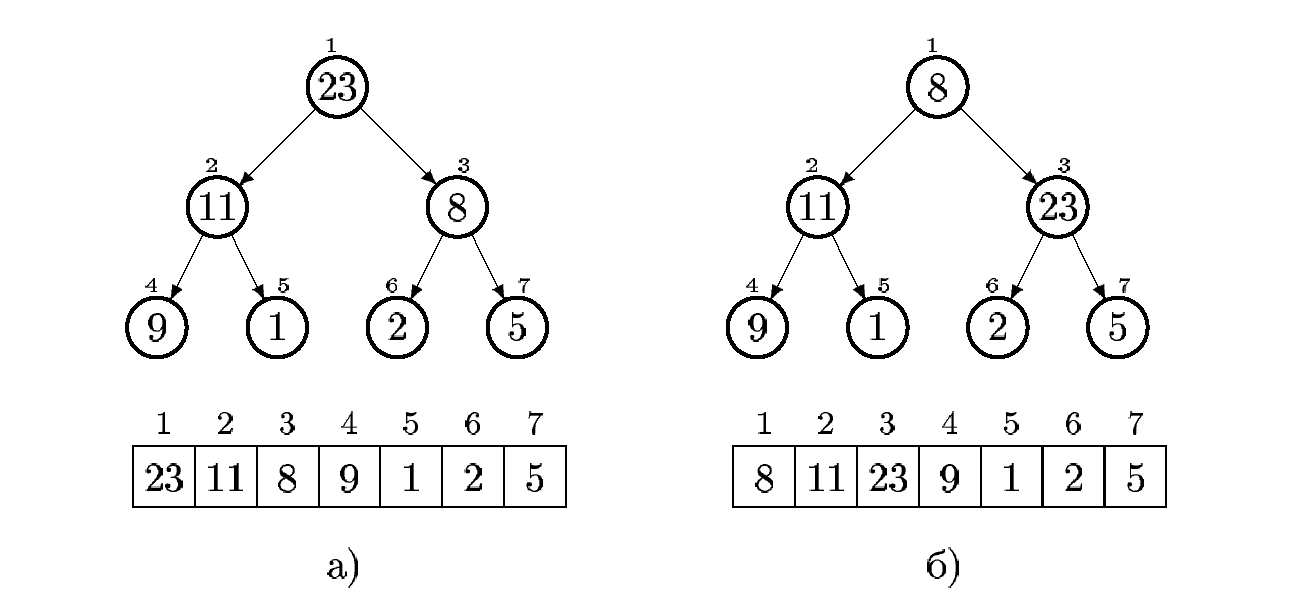
Рисунок 3.1 - Приклад упорядкованого а) і частково впорядкованого б) двійкових дерев й їхнє подання на масиві.

Основна операція при роботі з купою ‑ перетворення частково впорядкованого дерева в повністю впорядковане. Цю дію виконує рекурсивна процедура Heapify, параметрами якої є масив A(n), на перших k елементах якого розміщується частково впорядковане двійкове дерево, і індекс i ─ корінь деякого піддерева, з яким буде працювати процедура. Зокрема, Heapify(A,n,1) буде обробляти дерево, представлене на всьому масиві. Ідея алгоритму Heapify, що реалізує цю процедуру, проста: якщо властивість (4.1) для вершини i не виконується, то елемент a_i варто поміняти з більшим з його дітей, лівим (left) або правим (right), і т.д., поки він не займе своє місце в дереві.

Proc Heapify(A(n),k,i)

left = 2i right = 2i+1

if (left ≤ k) and (a_left >a_i) then largest = left

else largest = i

if (right ≤ k) and (a_right > a_largest) then largest = right

if largest ≠ i then begin

a_i ↔ a_largest

Heapify(A,k,largest)

endif

End Heapify

Оскільки висота дерева з n елементів є h=[log₂(n+1)], а на кожному кроці ми спускаємося по дереву на один рівень, то тимчасова складність процедури Heapify становить O(h)=O(log₂n).

Тепер розглянемо завдання побудови купи із заданого масиву A(n). Для цього будемо послідовно застосовувати процедуру Heapify для впорядкування всіх піддерев, починаючи з мінімальних і поступово їх укрупнюючи. Оскільки вершини з номерами не мають нащадків, те піддерева із цими вершинами як коріння тривіально впорядковані. Тому починати треба з вершини з номером , рухаючись до початку масиву. Коли буде досягнутий корінь дерева (елемент із індексом 1), все дерево буде впорядковано.

Proc BuildHeap(A(n))

for i = [n/2] downto 1 do Heapify(A,n,i)

End BuildHeap

Процедура Heapify викликається =O(n) раз, а кожне її виконання вимагає часу O(log₂n), тому час роботи процедури BuildHeap не перевищує O(nlog₂n). Однак, цю оцінку можна поліпшити. Оскільки час роботи процедури Heapify залежить від висоти вершини, для якої вона викликається (і пропорційна цій висоті), дійсна тимчасова складність процедури BuildHeap становить O(n).

Алгоритм сортування масиву A(n) за допомогою купи складається із двох частин. Спочатку викликається процедура BuildHeap, після виконання якої масив стає купою. Ідея другої частини проста: після впорядкування максимальний елемент масиву перебуває в корені дерева (елемент a₁). Його варто поміняти місцями із самим останнім (правим) вузлом у дереві (елемент a_n), зменшити дерево на одну (останню) вершину й застосувати процедуру Heapify до дерева, що залишилося, щоб перетворити його в упорядковане. Після цього в корені буде максимальний із n-1 елементів, що залишилися. Так треба повторювати доти, поки в купі не залишиться всього один елемент ‑ корінь дерева. Цей алгоритм реалізується процедурою HeapSort.

Proc HeapSort(A(n))

BuildHeap(A)

k = n

for i = n downto 2 do

a₁ ↔ a_k

k = k-1

Heapify(A,k,1)

endfor

End HeapSort

Час роботи HeapSort становить O(nlog₂n). Дійсно, перша частина (побудова купи) вимагає часу O(n), а кожне з (n-1) виконань циклу for забирає час O(log₂n).

Розглянемо також алгоритм швидкого сортування. Він вважається одним з найбільш ефективних з відомих на даний момент і тому використовується набагато частіше за всі інші. Хоча в найгіршому разі він сортує масив n за час O(n²), у середньому (для випадкового набору даних) час роботи становить усього O(nlog₂n), причому для цього алгоритму характерні винятково короткі внутрішні цикли. Алгоритм швидкого сортування відносно нескладно запрограмувати, і він добре працює на різних видах вхідних даних. Недоліком алгоритму є, звичайно, можливий час виконання O(n²).

Ідея швидкого сортування: ділимо масив на дві частини й сортуємо їх незалежно один від одного. На рис. 3.2 показано, як масив ділиться щодо першого (граничного) елемента t так, щоб збирати всі елементи, менші t, на відрізку a_l+1,…,a_i, а більші t – на відрізку a_j,…,a_r... Спершу обидва відрізки «порожні»:

i=(l+1)-1= l,

j=r+1

Головний цикл алгоритму містить два вкладених цикли. Перший зрушує i вправо до знаходження елемента, більшого t, а другий зрушує вліво j, пропускаючи елементи, більші t, і зупиняючись на меншому. Очевидно, два елементи, у які “уперлися” індекси i й j стоять не на своїх місцях. Головний цикл міняє їх місцями, перевіряючи заодно умову закінчення обробки масиву i<j.

По закінченні чергової ітерації, елемент, щодо якого робилося розподылення, стає на границю двох розбитих областей («встановлюється на місце», звідки його вже не знадобіться рухати)

Рисунок 3.3 - Сканування й розбиття підмасива елементом t.

Після розбивки n елементів приблизно половина з них виявиться нижче виділеного елемента, а половина – «вище». За цей же самий час, наприклад, алгоритм вставки встановлює на місце тільки один елемент. Алгоритм QSort реалізує швидке сортування з описаною схемою розбивки Хоара.

Proc QSort(l,r)

if (l ≥ r) return

t = a_l

i = l

j = r+1

while True do

do i=i+1 while ((i r) and (a_i<t))

do j=j-1 while a_j ≥ t

if i>j then break

a_i a_j

endwhile

a_l a_j

QSort (l,j-1)

QSort (j+1,r)

End QSort

Розглянемо ще один клас логарифмічних алгоритмів, основою яких є операція «злиття» (merging), тобто об'єднання двох відсортованих масивів в один.

Отже, розглянемо два відсортованих по неубуванню масиви X(n) і Y(m). Нехай необхідно об'єднати їх в один масив Z(n+m), також упорядкований. Вирішимо це завдання в такий спосіб: з кожної пари мінімальних елементів масивів X й Y (починаючи з x₁ й y₁) вибираємо найменший і записуємо його в Z, а в масиві, з якого був узятий цей елемент, збільшуємо на одиницю індекс до наступного, ще не розглянутого елемента. Так продовжуємо, поки один з масивів не вичерпається. Якщо першим вичерпався масив X, то залишок Y цілком переписуємо в Z, якщо першим вичерпався Y, те в Z переписуємо залишок X (див. рис.3.4).

Рисунок 3.4 – Приклад роботи алгоритму SimpleMerge. Жирним шрифтом зазначені порівнювані на даному кроці елементи; оброблені елементи замінені на косу рису

Proc SimpleMerge(X(n),Y(m))

i = 1

j = 1

for k = 1 to n+m do

if i = n then

z_k = y_j

j = j + 1

continue

endif

if j = m

z_k = x_i

i = i + 1

continue

endif

if x_i < y_j

z_k = x_i

i = i + 1

else

z_k = y_j

j = j + 1

endif

endfor

End SimpleMerge

Головний недолік цього алгоритму – наявність на кожному витку циклу двох перевірок на вичерпання масивів X й Y. У більшості випадків (якщо nm) ці умови не виконуються й перевірка робиться вхолосту. Позбудемося від зайвих перевірок: створимо інший масив Т(n+m), і послідовно перепишемо в нього два наявні масиви X(n) і Y(m) так, щоб елементи х_i йшли в прямому порядку, а y_j – у зворотному (див. рис. 3.5).

Тепер, починаючи із двох кінців масиву T, з пари крайніх елементів вибираємо найменший і записуємо його в Z (аналогічно SimpleMerge). Найбільший елемент обох масивів у цьому випадку буде природним обмежником, на якому зійдуться покажчики на крайні неопрацьовані елементи T.

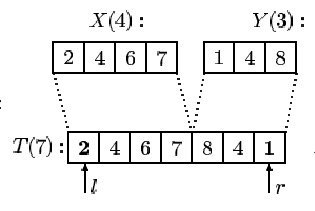
Рисунок 3.5 - Формування буферного масиву для виконання операції злиття

Proc BitonicMerge

for l=n downto 1 do t_l=x_l

for r=n+1 to n+m do t_r=y_n+m+1-r

for k=1 to n+m do

if t_l < t_r then

z_k = t_l

l = l + 1

else

z_k = t_r

r = r - 1

endif

endfor

End BitonicMerge

Описаний алгоритм злиття BitonicMerge є, по суті, базовим для рішення завдань сортування, до яких ми тепер і переходимо.

Отже, сортування злиттям виконується в такий спосіб. Щоб відсортувати заданий масив A(n), ми розділимо його на дві частини a₁,…,a_[n/2] і a_[n/2]+1,…,a_n, виконаємо рекурсивне сортування обох частин, а потім зробимо їхнє злиття. Алгоритм MergeSort реалізує цей метод.

Proc MergeSort(A,l,r)

if r  l return

m = [(r+l)/2]

MergeSort(A,l,m)

MergeSort(A,m+1,r)

Merge(A,l,m,r)

End MergeSort

Proc Merge(A,l,m,r)

for i=m downto l do t_i=a_i

for j=m+1 to r do t_j=a_r+m-j+1

for k=l to r do

if t_i < t_j

a_k = t_i

i = i + 1

else

a_k = t_j

j = j - 1

endif

endfor

End Merge

Рекурсивні алгоритми, як правило, компактні й зрозумілі. У той же час, такий підхід настільки «жадібний» до пам'яті, що його реалізація може стати практично неможливою. Тому пропонується розглянути також нерекурсивну реалізацію сортування масиву злиттям.

Proc MergeSortSimple

m=1

while (m <= r-1) do

i=l

while (i <= r-m) do

Merge(A,i,i+m-1, min(i+m+m-1,r))

i=i+m+m

endwhile

m=m+m

endwhile

End MergeSortSimple

Розглянуті в цьому розділі алгоритми сортування мають складність Nlog₂N, що не залежить від структури вихідних даних. Це принципово відрізняє їх від швидкого сортування й від багатьох інших алгоритмів, час роботи яких може істотно залежати від характеру вхідних даних (упорядкований або назад упорядкований вхідний масив, рівномірний, випадковий і т.д.).