9.3 Прогнозирование на основе укрупнения, скользящих средних и экстраполирующих линейных функций

Способы обработки ряда динамики: укрупнение, сглаживание (механическое, по скользящей средней, аналитическое), смыкание, интерполяция, экстраполяция и др.

Смыкание – прием объединения двух рядов динамики – уровень ряда за период, когда произошли изменения в структуре изучаемого явления или другие радикальные изменения, принимается за базу (100%) относительно которой пересчитываются значения остальных уровней первого и второго ряда; затем строится ряд с пересчитанными к общей базе уровнями.

Укрупнение – прием объединения нескольких уровней интервального ряда. Укрупнение уровней можно проводить путем перехода от ежемесячных данных к квартальным, от квартальных данных к полугодовым и т.д.. При этом следует учесть вид рядов динамики и решить вопрос о том, как получить новые уровни рядов: суммированием или осреднением их уровней.

Механическое сглаживание осуществляется на основе начального уровня и среднего абсолютного прироста:

Метод сглаживания по левой и правой половине производится путем нахождения среднего значения по левой половине, по правой половине и соединяют их между собой.

Сглаживание по скользящей средней в принципе возможно по трем, четырем, пяти и т.д. уровням исходного ряда, то есть по трех-, четырех-, пятичленной скользящей средней.

Выбор интервала сглаживания, с одной стороны, зависит от длины исходного ряда. При сглаживании по пятичленной (и более длинной) средней в исходном ряду динамики может не оказаться достаточного количества уровней. Необходимо, чтобы сглаживание ряда динамики не привело к вырождению исходного ряда в одну точку. Для расчета пятичленной скользящей средней их должно быть не меньше шести. Каждый уровень нового ряда должен соответствовать интервалу сглаживания и находиться в его центре. Таким образом, интервал сглаживания «скользит» по исходному ряду динамики.

С другой стороны, при большом количестве уровней исходного ряда динамики слишком узкий интервал сглаживания может оказаться недостаточным для выявления тенденции в исходном ряду динамики, а довольно широкий интервал сглаживания - привести к ее исчезновению.

Количество рассчитанных по скользящей средней уровней нового ряда будет меньше, чем в исходном ряду динамики. Так, сглаживание по трехчленной скользящей средней «укорачивает» исходный ряд динамики на два уровня, сглаживание по пятичленной скользящей средней – на четыре уровня и т.д.

При сглаживании по трехчленной скользящей средней значения двух исчезнувших крайних точек можно вычислить по эмпирическим формулам. Крайняя левая точка нового ряда определяется как:

У_-1= (5У₁+2У₂-У₃)/6 (9.11)

Крайняя правая точка нового ряда рассчитывается по формуле:

У₊₁= (-У₂+2У₃ +5У₄)/6 , (9.12)

где У_-1 и У₊₁- крайняя левая и крайняя правая точки нового ряда,

У₁, У₂ ,У₃ ,У_n-2, У_n-1, У_n – три первых и три последних уровня исходного ряда динамики.

Сглаживание по среднему абсолютному приросту и среднему коэффициенту роста проводится по формулам:

У_i = У₁ + ( i-1), (9.13)

У_i = У₁ * К_р^i-1 . (9.14)

Аналитическое сглаживание производится на основе метода наименьших квадратов.

Для сглаживания ряда динамики с четным количеством уровней (точек) методом наименьших квадратов целесообразно построить вспомогательную таблицу, введя для каждого исходного периода условные обозначения t усл. так, чтобы их сумма была равна нулю. Ниже приведен пример для четырех точек исходного ряда

Для сглаживания ряда динамики по методу наименьших квадратов целесообразно построить вспомогательную таблицу, введя для каждого исходного периода условные обозначения t усл.

Таблица 3 – Аналитическое сглаживание

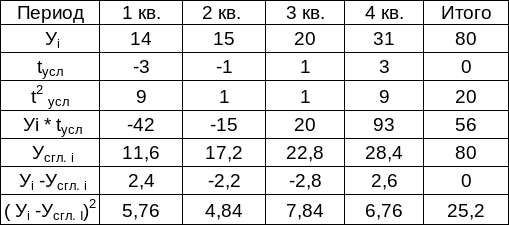
В таблице 3 сглаженные уровни У _сгл.i для каждого i-го периода получены на основе расчетов У _сгл.i = А + В * t _усл. Коэффициенты регрессии А и В определяют из системы уравнений:

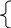n*А + В  t _усл =  У I (9.15)

A  t + B  t ² _усл =  У _i t _усл

Эта система при  t _усл. = 0 сводится к более простой

n*А =  У I (9.16)

B  t² _усл =  У _i t _усл

Для наилучшего сглаживания можно подобрать функцию, для которой

 (У _сгл.i - У i)² = min. (9.17)

Метод экстраполяции применяется для нахождения неизвестных уровней ряда за его пределами. Экстраполяция используется в прогнозировании

Интерполяция – нахождение неизвестного уровня ряда внутри него.. При интерполяции пользуются методом средних величин. Неизвестный уровень ряда рассчитывают как среднюю арифметическую из рядом стоящих с ним уровней ряда. Данный метод прост, но менее точен. Более точным является метод наименьших квадратов.

7.3 Прогнозирование на основе нелинейных экстраполирующих функций

Прогнозирование по среднему коэффициенту роста проводится по формуле:

У^к _i = У_{n *} к _р , (9.18)

где У^пр _i – прогнозируемый i -й уровень ряда;

к _р– средний коэффициент роста ряда динамики.

Прогнозирование ряда динамики методом наименьших квадратов (МНК) или аналитическим методом проводят путем построения теоретической линии регрессии. Теоретическая линия регрессии строится на основе подбора аппроксимирующей функции, для которой достигается:

 (У _{сгл .i} - У _i ) ² = min. (9.19)

Если теоретическая линия регрессии – гипербола вида У _i = А + В / t _i, то коэффициенты регрессии А и В определяют из системы уравнений:

n*А + В  (1/t _i) =  У _I (9.20)

A (1/ t _i )+ B (1/ t _i )² =  (У _i /t _i )_,

где n – число точек исходного ряда динамики.

В качестве аппроксимирующих функций для построения линий тренда зачастую используются:

парабола второго порядка У _i = А + В * t _i+ С * t _i² ,

парабола третьего порядка У _i = А + В * t _i+ С * t _i² + D * t _i^{3 ,}

показательная функция У _i = А * В ^t_.

Лекция 18 Статистическая методология национальных счетов, балансов и системы показателей, характеризующих экономические процессы на макроуровне

18.1 Понятие СНС, её состав

18.2 Основные принципы составления национальных счетов

18.3 Границы производства в СНС

18.4 Институциональные сектора в СНС