8.2 Индексный метод анализа влияния факторов

Одним из методов индексного анализа является анализ влияния изменения индексируемой величины и структуры явления на изменение показателя. Этот метод применяют при изучении качественных показателей таких, как средняя заработная плата, средняя производительность труда и т.д.

Индексы качественных показателей рассчитываются в тех случаях, когда осредняют средние величины, например, на основе данных о средних уровнях производительности труда в каждом цехе необходимо рассчитать средний уровень производительности труда в целом.

При этом могут быть следующие ситуации:

При увеличении производительности труда в каждом цехе в текущем периоде по сравнению с базисным, в целом по заводу может произойти снижении производительности труда, и наоборот при уменьшении показателя в каждом цехе, в целом по предприятию он может увеличиться. В этом состоит статистический парадокс. Он объясняется влиянием структурных сдвигов. Для раскрытия явления статистического парадокса рассчитывают следующие индексы:

• индекс переменного состава,

• индекс постоянного состава,

• индекс структурных сдвигов.

1) Индексы переменного состава бывают двух видов:

А) индексы средних уровней

(8.7)

где Т1 – численность сотрудников в отчетном периоде.

Б) агрегатные индексы:

. (8.8)

2) Индекс постоянного состава

(8.9)

или

(8.10)

3) Индекс структурных сдвигов

(8.11)

Между индексами переменного, постоянного состава и структурных сдвигов существует взаимосвязь:

= х (8.12)

= (8.13)

или . (8.14)

Лекция 9Анализ рядов динамики

9.1Понятие и виды рядов динамики

9.2Показатели рядов динамики

9.3 Прогнозирование на основе укрупнения, скользящих средних и экстраполирующих линейных функций

9.1 Понятие и виды рядов динамики

Ряд значений статистического показателя, расположенных в хронологическом порядке и характеризующих развитие явления во времени, называется рядом динамики. Динамический ряд состоит из двух элементов: момента или временного периода (t), по отношению к которому приводятся статистические данные, и статистического показателя, характеризующего размер рассматриваемого явления в соответствующий период времени, называемый уровнем динамического ряда (у).

В зависимости от того, в каких единицах выражены уровни ряда, ряды динамики бывают рядами абсолютных величин, относительных и средних величин.

По виду временного показателя динамические ряды бывают моментные и интервальные. Если уровни приводятся по состоянию на определенную дату, то такой ряд называют моментным рядом динамики. Моментные ряды динамики бывают с равноотстоящими уровнями и неравноотстоящими уровнями. В интервальных рядах динамики каждый уровень относится к определенному промежутку (интервалу) времени. Интервальные ряды динамики бывают с равными и неравными интервалами.

Вид ряда динамики влияет на выбор формул расчета его показателей.

Средний уровень ряда. Если дан моментный ряд с равными промежутками между датами, то для определения среднего уровня применяется формула средней хронологической взвешенной:

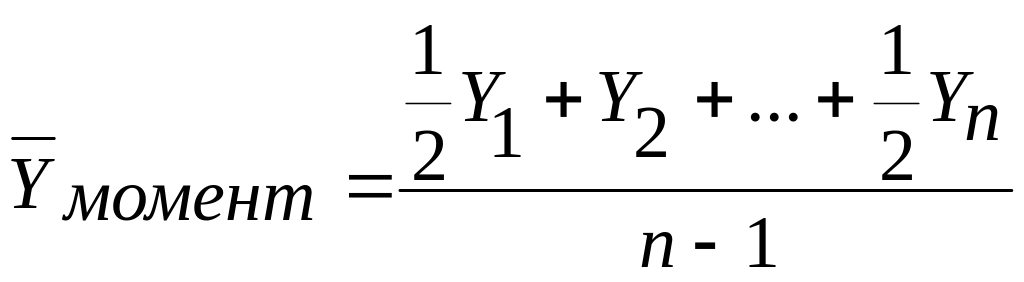(9.1)

Если в качестве уровней моментного динамического ряда взяты даты изменения показателя, то расчет среднего уровня следует проводить по формуле средней арифметической взвешенной, в качестве весов в которой используются временные промежутки между соседними датами.

Средний уровень интервального ряда при равных и неравных интервалах определяется соответственно по формулам:

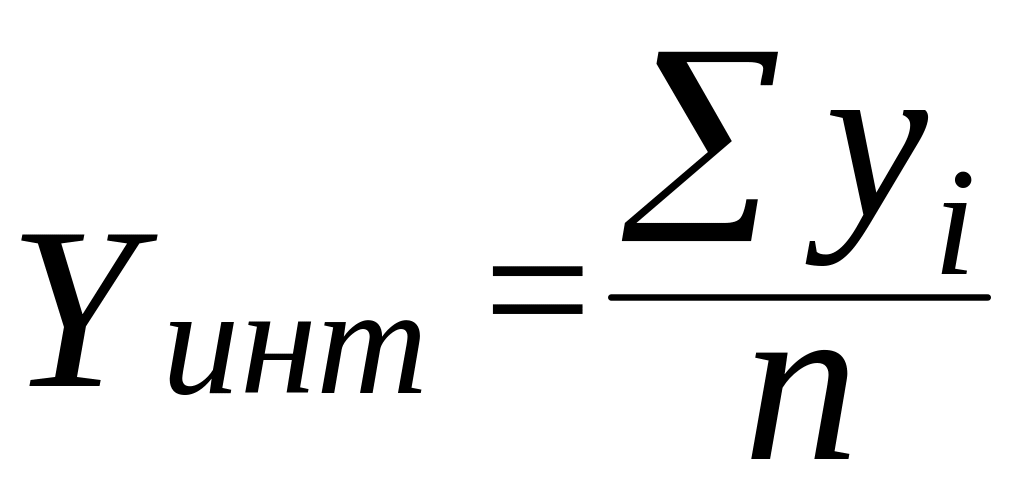, (9.2)

где y_i = y _j , i, j = 1, 2,…, n ,

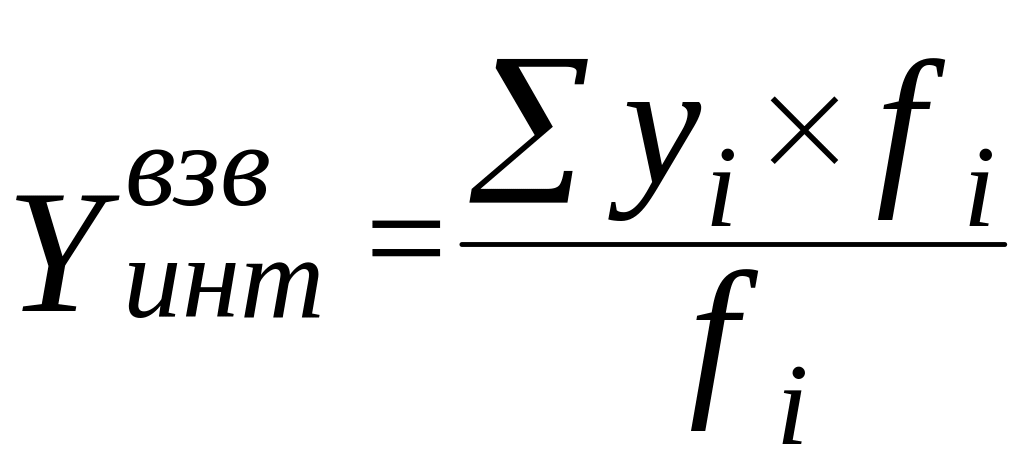, (9.3)

где f _i - длина интервала для уровня y_i и y_i ≠ y _j .

Абсолютный прирост – это разность между двумя уровнями ряда. Если сравнение происходит с одним и тем же уровнем ряда, то это базисные абсолютные приросты, если с предыдущим – цепные.

Средний абсолютный прирост рассчитывается по формуле:

 = ( У _n - У₁ ) / ( n -1) (9.4)

Средний коэффициент и темп роста равны:

К _р = (У _{n /} У₁ ) ^{1 / ( i - 1),} (9.5)

Т _р = К _{р *} 100% (9.6)

Средний коэффициент и темп прироста определяют соответственно:

К _{п р} = К _{р_} ⁻ 1, (9.7)

Т пр = Т р - 100%. (9.8)

Для двух рядов динамики рассчитывают коэффициент опережения:

К_оп = у_i1 / у_{i п}, (9.9)

где уi₁ и уi _п - уровни первого и второго сравниваемых рядов динамики за один и тот же период (момент) времени.

Один процент абсолютного прироста ‌ 1 % ‌ рассчитывается по формуле:

‌ 1% ‌ = ∆ i ⁄ Т _{п р i} = у _i-1 /100 . (9.10)