7.3 Относительные показатели вариации

Для сравнения вариации одного и того же показателя, но применительно к разным совокупностям, используют относительные показатели вариации. К ним относятся: коэффициент осцилляции, относительное линейное отклонение и коэффициент вариации.

Наибольшее практическое применение получил коэффициент вариации. Он рассчитывается как отношение среднего квадратического отклонения к средней арифметической величине того же признака.

Если коэффициент вариации, выраженный в процентах, меньше 33% (по мнению некоторых авторов меньше 35- 40%), то статистическая совокупность считается однородной.

Лекция 8 Корреляционный и индексный методы анализа

8.1 Корреляционный метод анализа влияния факторов

8.2 Индексный метод анализа влияния факторов

8.1 Корреляционный метод анализа влияния факторов

Стохастические (корреляционные) связи. Стохастические связи проявляются в виде корреляции между значениями. Для их изучения применяются графический метод, метод сравнения параллельных рядов, метод аналитических группировок и регрессионно-корреляционный анализ.

Регрессионный анализ позволяет выявить вид связи, а корреляционный - установить тесноту (силу) связи.

Для линейных зависимостей теснота связи определяется с помощью коэффициента корреляции, а для нелинейных - с помощью индекса корреляции (корреляционного отношения).

Для расчета коэффициента корреляции используются различные формулы, но все они выводятся из одной и той же формулы.

, (8.1)

где  _х и  _у - среднеквадратические отклонения Х и У, рассчитанные по сгруппированным данным:

 ( Х _k – X _общ)² _* f _k

 _х = _; (8.2)

 f _k

 ( У _k – У _общ)² _* f _k

 _у = _. (8.3)

 f _k

Теоретическое корреляционное отношение рассчитывают по формуле:

 =  ( У_{Х k} – У _общ)² _* f _{k ,} (8.4)

 ( У _k – У _общ)² _* f _k

где У_{Х k} - выравненные значения результативного признака, то есть рассчитанные по уравнению регрессии при Х = X _к.

Значение r, n находится в пределах от -1 до +1 -1

Чем ближе значение r к единице, тем теснее связь W факторами х и у. Если эти коэффициенты < 0, это говорит об обратной связи между факторами х и у. Если х и у = 0, то связь между ними отсутствует.

Чтобы определить тесноту связи пользуются таблицей Чэддока.

При r = 1 - связь функциональная.

Корреляционное отношение являются более универсальным показателем, его можно рассчитывать и для линейных связей.

Для оценки тесноты связи между качественными показателями (например, работа по специальности, наличие жилья и т.п.) применяют непараметрические методы оценки корреляционной связи факторов. К непараметрическим методам относятся оценка связи на основе расчета коэффициентов ассоциации и контингенции. Для этого предварительно составляют таблицу, на пересечении строк и столбцов которой находятся числа, равные количеству единиц статистической совокупности с соответствующими значениями первого и второго признака.

Таблица 1 – Таблица значений качественных признаков

Первый признак	Второй признак
	Первое значение	Второе значение	Итого
Первое значение	а	b	а+b
Второе значение	с	d	c+d
Итого	а+с	b+d

По итоговым данным таблицы 1 рассчитывают коэффициент ассоциации либо коэффициент контингенции:

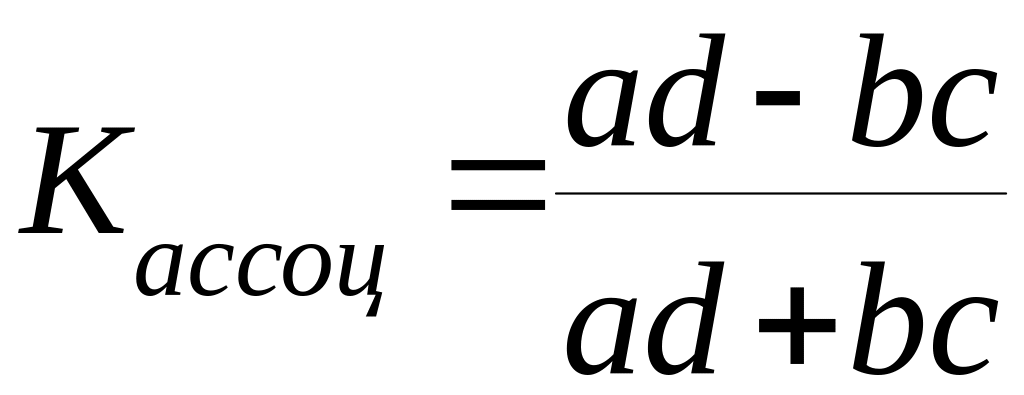, (8.5)

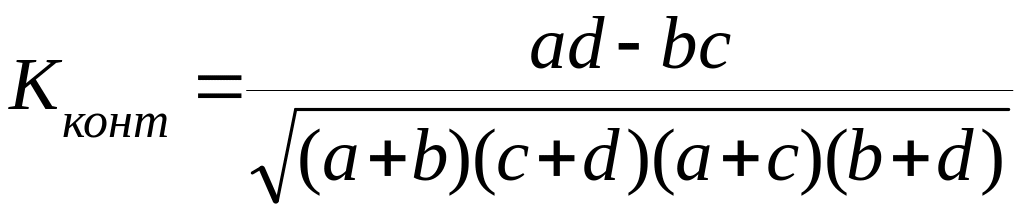. (8.6)

Если эти коэффициенты < 0.3, то связи между признаками нет.

Преимущество первого показателя состоит в том, что он единственный из всех показателей тесноты связи вполне определенно позволяет ответить на вопрос о характере связи между двумя признаками (прямопропорциональна она или обратнопропорциональна).

Зависимость между признаками может быть парной и многофакторной. В последнем случае на один и тот же признак у, оказывает влияние несколько факторных признаков, т.е. .