6.3 Средние показатели структуры

Мода (Мо) — это наиболее часто встречающееся значение признака в статистической совокупности или значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по разному.

В дискретных вариационных рядах мода – это признак, которому соответствует наибольшая частота.

В зависимости от того, равны интервалы между собой или нет, применяют тот или иной подход к определению моды. Для определения моды в интервальных вариационных рядах с равными интервалами сначала по наибольшей частоте находят модальный интервал, затем рассчитывают моду по формуле:

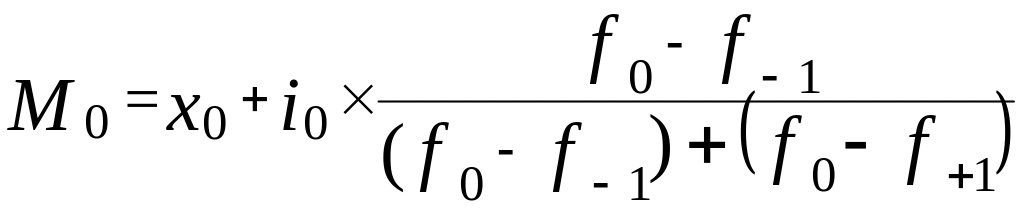, (6.13)

где – начало модального интервала,

– длина модального интервала,

– частоты интервалов, стоящих перед модальным, модального и после модального.

Для получения более полной характеристики вариационного ряда помимо средней величины и моды рассчитываются так называемые структурные показатели. К ним относятся медиана, квартили, децили и перцентили.

Медианой (Me) является значение варианты, находящейся в центре упорядоченной по возрастанию значений признака совокупности. Медиана делит вариационный ряд на две равные части. При этом 50% единиц совокупности имеют значение меньше медианного, а 50% - больше медианного.

В дискретном ряду распределения медиана находится по номеру. Номер медианы находится по формуле:

, (6.14)

где n – число единиц в совокупности.

При четном количестве единиц в совокупности медиана получается путем расчета средней арифметической из двух рядом стоящих значений признаков.

В интервальном ряду распределения медиана рассчитывается по формуле:

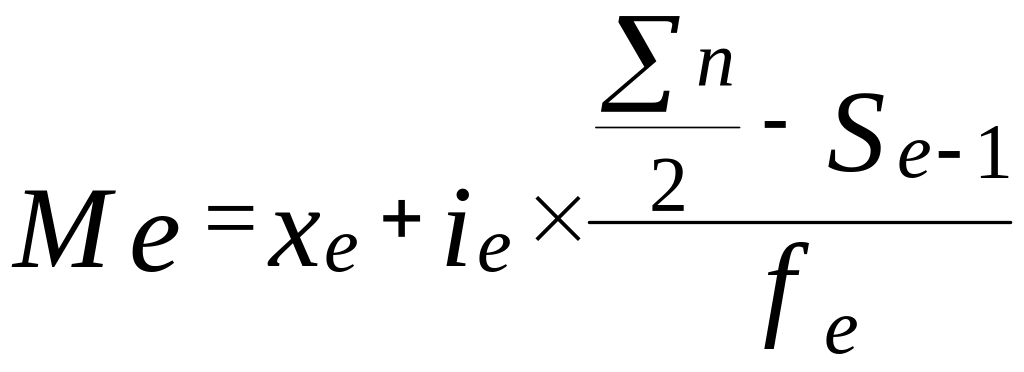, (6.15

где - начало медианного интервала,

– длина медианного интервала,

– сумма накопленных частот до интервала, в котором находится медиана,

– частота медианного интервала.

Медиана имеет свойство, благодаря которому используется в экономических и коммерческих расчетах:

(6.16)

В нормальных рядах распределения мода и медиана совпадают со средним арифметическим значением.

Квартили, квинтили, децили и перцентили относятся к группе квантилей.

Квантили — это показатели, которые делят вариационные ряды на равные по численности единиц части. Квартили делят упорядоченный вариационный ряд на четыре равные части: первый квартиль является значением, которого не превышают 25% единиц совокупности, второй квартиль - 50% (он совпадает с медианой), третий— 75%.

Квинтили делят упорядоченный вариационный ряд на пять равных частей, децили - на десять равных частей. Пятый дециль совпадает с медианой и вторым квартилем.

Перцентили делят упорядоченный вариационный ряд на сто равных частей.

Лекция 7 Вариационный анализ

7.1 Понятие о вариации в статистике и видах показателей вариации

7.2 Абсолютные показатели вариации

7.3 Относительные показатели вариации