2) Индекс постоянного состава

(5.25)

или

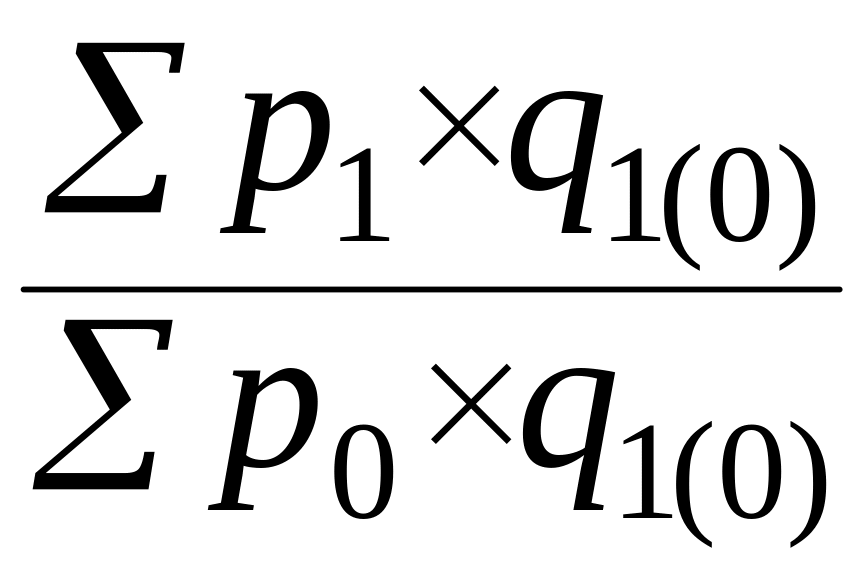(5.26)

3) Индекс структурных сдвигов

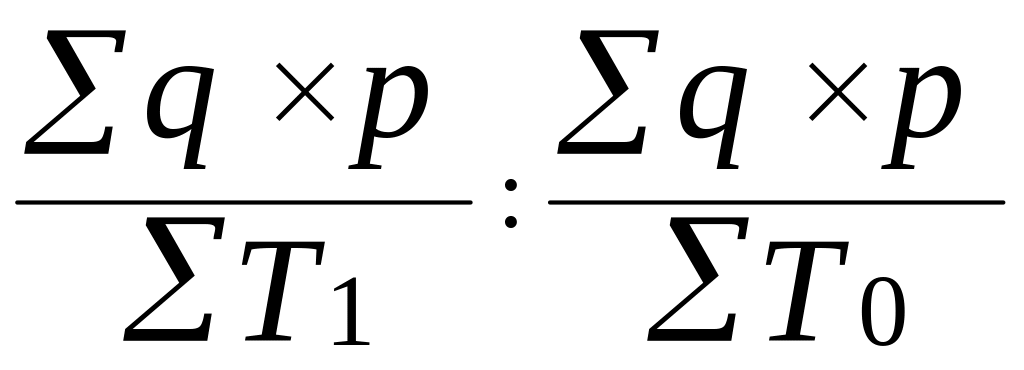(5.27)

Между индексами переменного, постоянного состава и структурных сдвигов существует взаимосвязь:

= х (3.59)

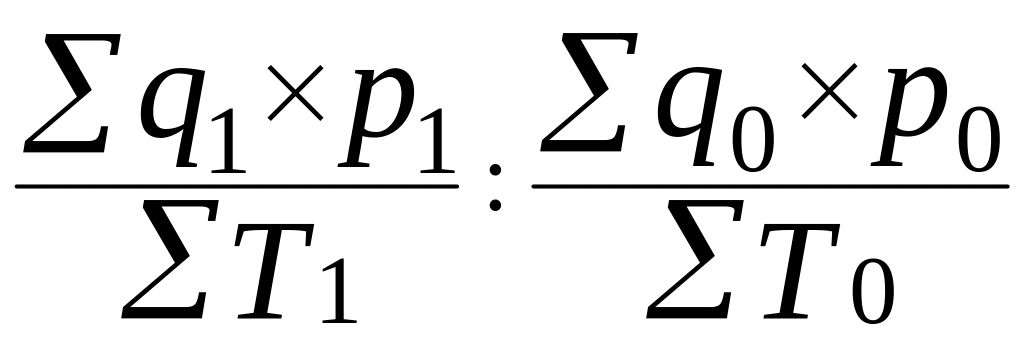= (3.60)

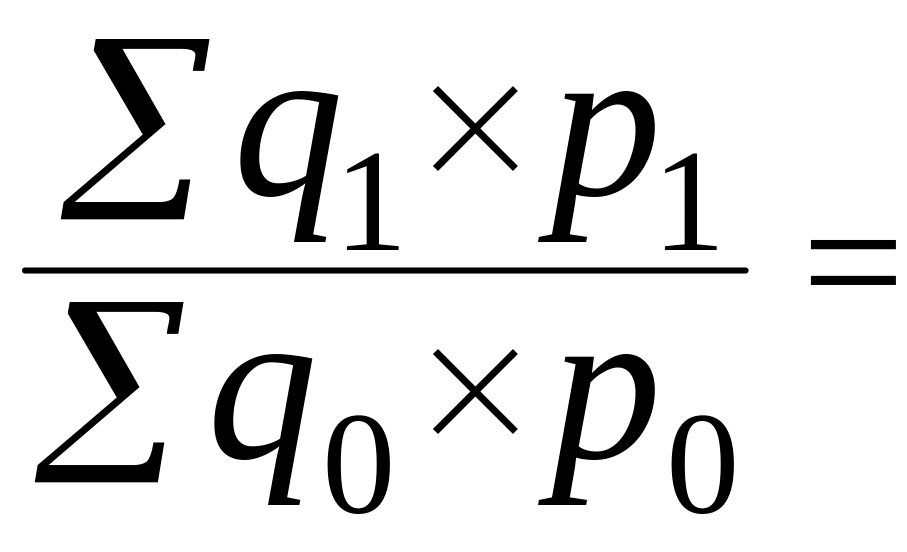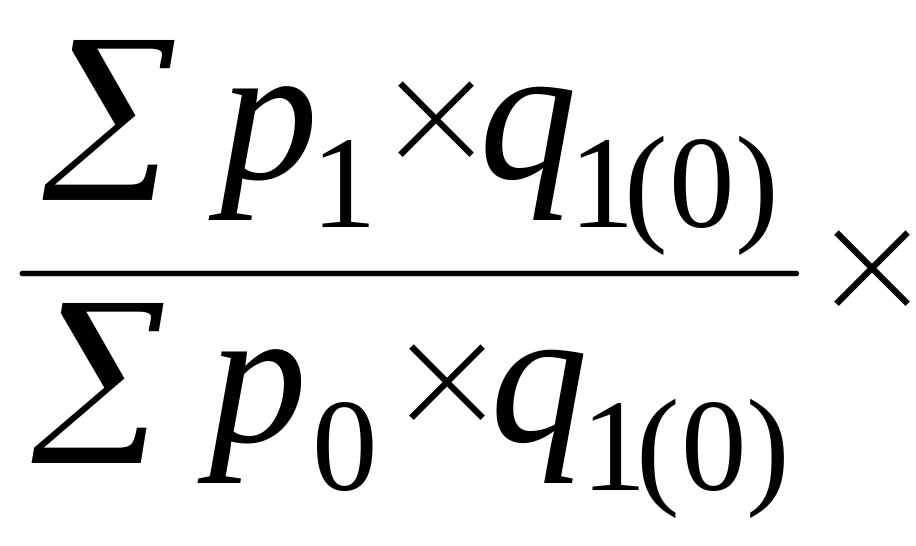
или . (3.61)

Лекция 6 Метод средних величин

6.1 Сущность статистических средних величин

6.2 Степенные средние величины

6.3Средние показатели структуры

6.1 Сущность статистических средних величин

Средняя статистическая величина – это типичная (обобщенная) характеристика, отражающая суть социально-экономического явления.

Существуют следующие виды статистических средних величин:

Степенные средние величины

- гармонические

- геометрические

- арифметические простые и взвешенные

- квадратические

- кубические

- биквадратические

и т.п.

Структурные средние

- мода

- медиана

- квартиль

- квинтиль

- дециль

- перцентиль (персентиль)

- и др.

Показатели вариации

- среднее линейное отклонение

- среднее квадратическое отклонение

- дисперсия

- коэффициент вариации

Средние индексы

- среднеарифметический индекс

- среднегармонический индекс

- среднегеометрический индекс

- индекс переменного состава

- индекс постоянного состава

- индекс структурных сдвигов

Средние показатели ряда динамики

- средний уровень

- средний абсолютный прирост

- средний коэффициент роста

- средний коэффициент прироста

- средний темп роста

- средний темп прироста

Другие виды средних показателей

- хронологическая средняя - антигармоническая средняя

- средняя ошибка выборки

• и др.

6.2 Степенные средние величины

Степенные средние величины получили свое название по виду функции, используемой для их расчета.

Если значения признаков в статистической совокупности не повторяются, степенную среднюю величину вычисляют в простой форме - это простая степенная средняя, при повторяющихся значениях – во взвешенной форме. Количество повторяющихся значений одного и того же признака ( Х _i ) называется его весом (f ).

Простая степенная средняя величина рассчитывается по формуле

Х^пр степ. = ( ) , (6.1)

где k – показатель степени средней величины.

При k = - 1 по данной формуле рассчитывают гармоническую среднюю величину (Х гарм.).

Е сли k 0 , на основе теории пределов по данной формуле определяют геометрическую среднюю величину ( Х геом. ).

Далее при k = 1 находят арифметическую среднюю, при k = 2 - квадратическую , при k = 3 - кубическую, при k = 4 - биквадратическую и т.д.

Если одно и то же значение признака встречается несколько раз, рассчитывают взвешенную среднюю величину:

Х^взв степ. = (∑ x f / ∑f ) , (6.2)

где f - это вес (частота значений признака x ).

Гармоническая средняя применяется если:

1 ) осредняемый признак является мерой времени и выражен в секундах и минутах.

2 ) осредняемая величина задана в виде функции неявного вида.

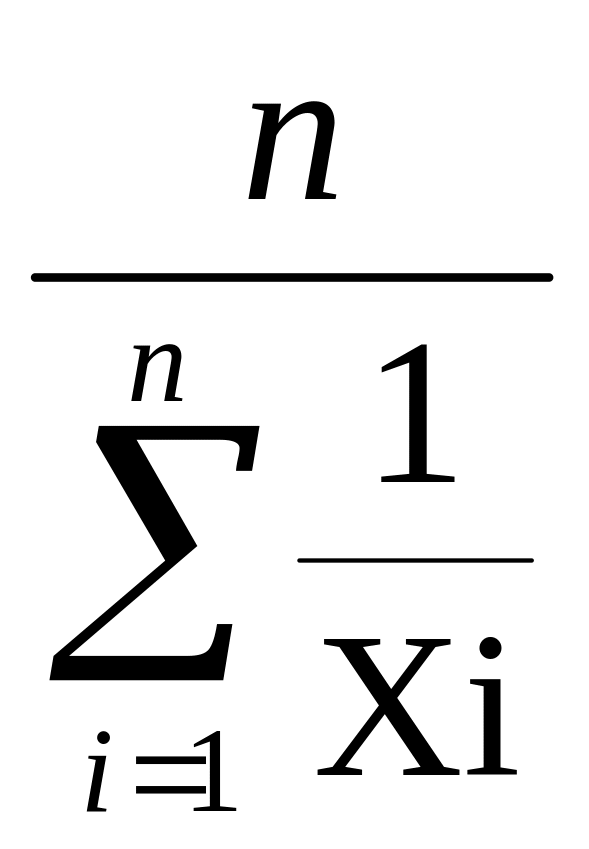= , (6.3)

где n – количество единиц в совокупности.

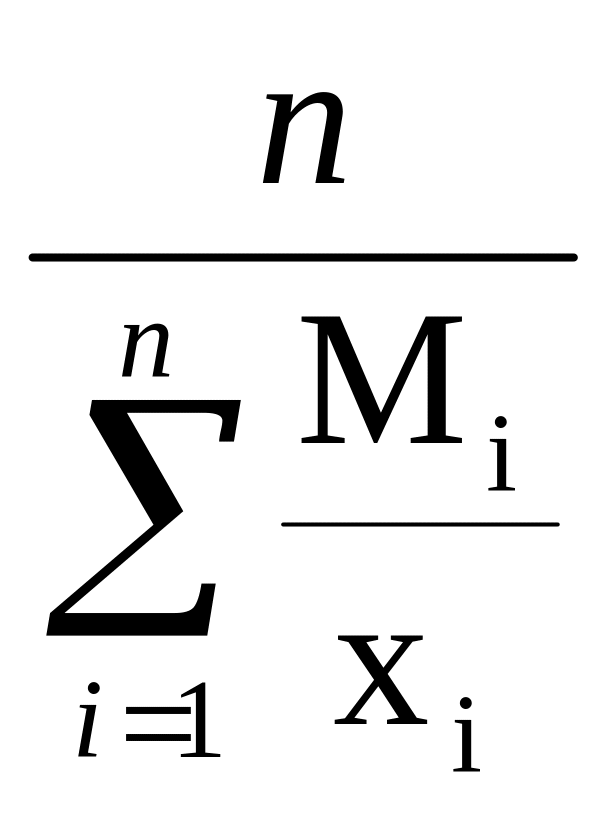= , (6.4)

где М = x f ,

Геометрическая средняя применяется при нахождении средних темпов или коэффициентов роста, т. к. она показывает во сколько раз в среднем одна величина в упорядоченной совокупности больше (или меньше) другой.

= , (6.5)

где n – число сомножителей (осредняемых значений признака).

= (6.6)

Арифметическая средняя определяется по формулам:

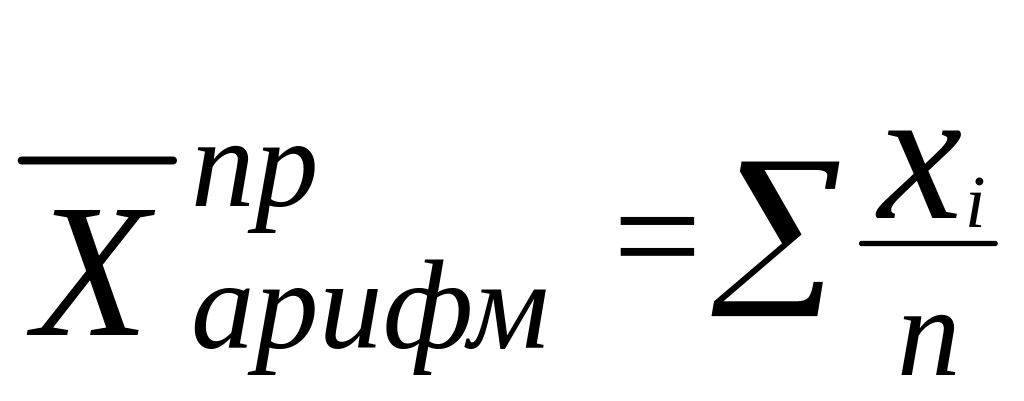(6.7)

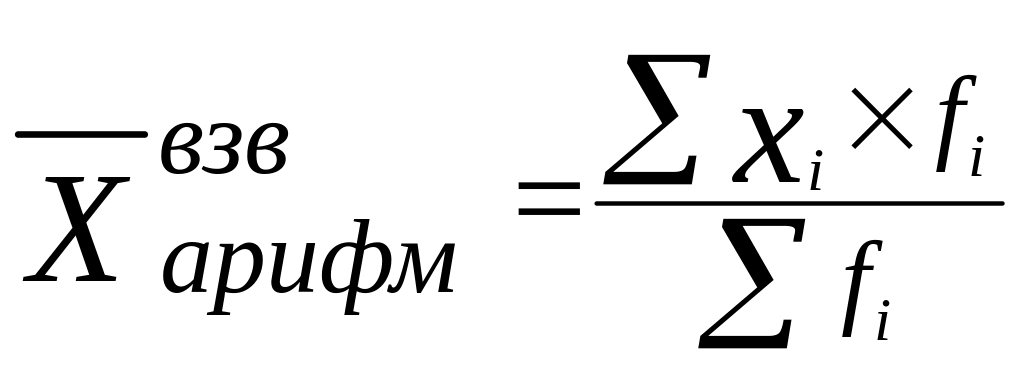(6.8)

Квадратическая средняя используется в тех случаях, когда осредняемая величина x задана в виде квадратической функции.

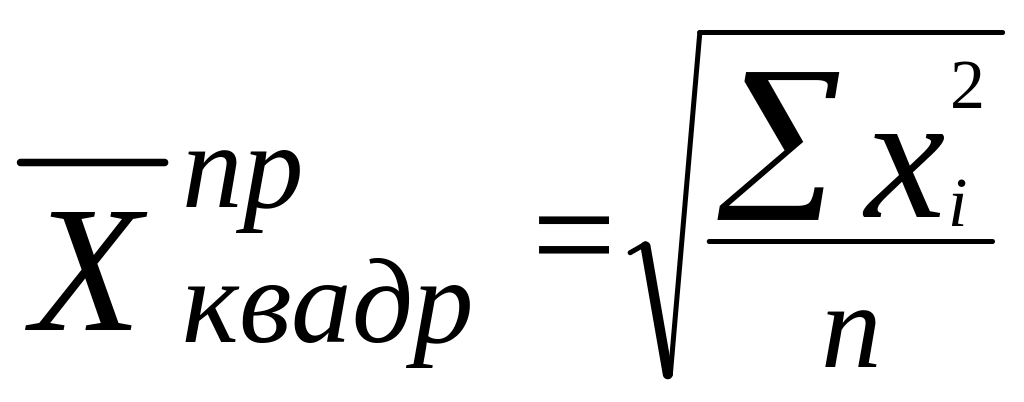(6.9)

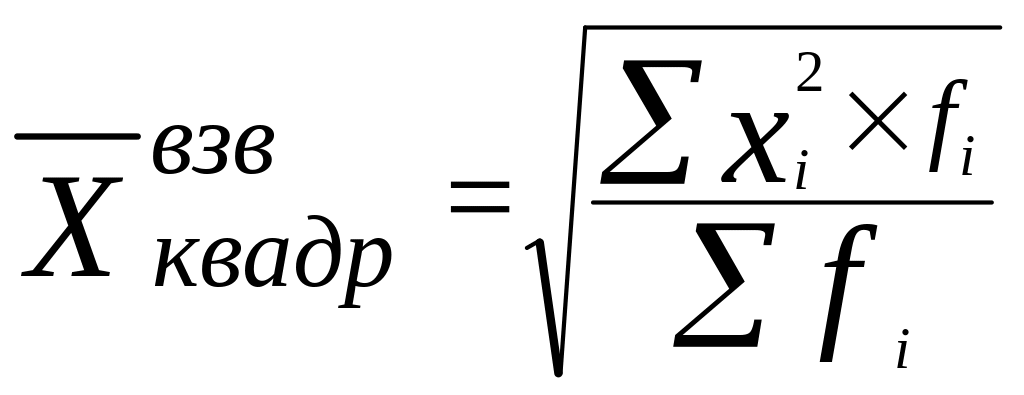(6.10)

Кубическая средняя применяется, если осредняемая величина задана в виде квадратической функции.

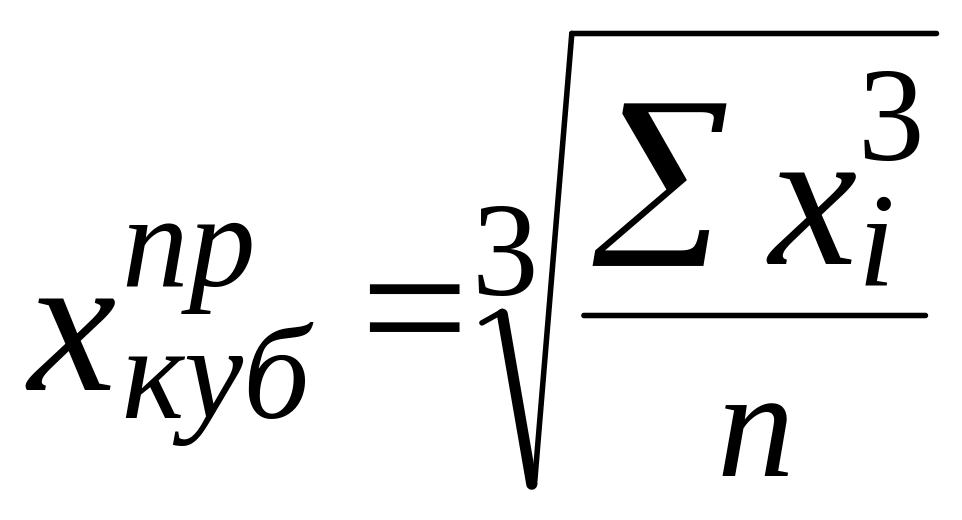(6.11)

(6.12)

Биквадратическая средняя рассчитывается как степенная средняя четвертого порядка и применяется при осреднении признака, являющегося функцией четвертого порядка.