2. Поле двух параллельных плоскостей, заряженных разноименно с поверхностными плотностями зарядов и .

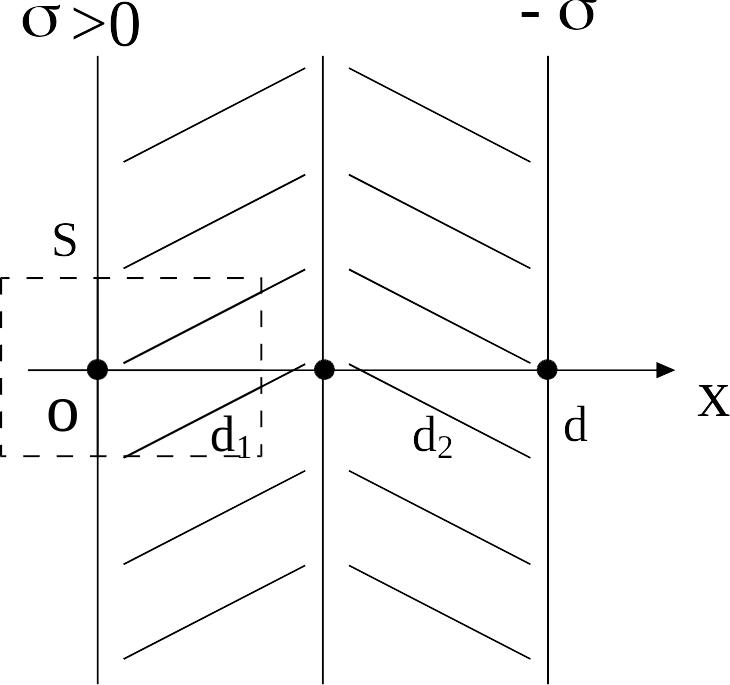- Пространство между пластинами заполнено двумя слоями диэлектриков,

- относительные диэлектрические проницаемости которых и ,

- а толщины и соответственно (рис.3).

Расстояние между пластинами равно , поэтому .

Из симметрии в распределении свободных зарядов на плоскостях и в расположении слоев диэлектрических сред ясно, что всюду векторы и должны быть параллельны оси , то есть , .

В каждом из слоев диэлектрика поле однородно. Поляризованы эти слои тоже однородно.

Поэтому в них имеются только поверхностные поляризованные заряды.

Плотности этих зарядов на плоских поверхностях каждого диэлектрика отличаются только знаком.

Напряженность поля связанных зарядов

• отлична от нуля только внутри самого слоя диэлектрика.

• Вне конденсатора (при и ) поля нет, , .

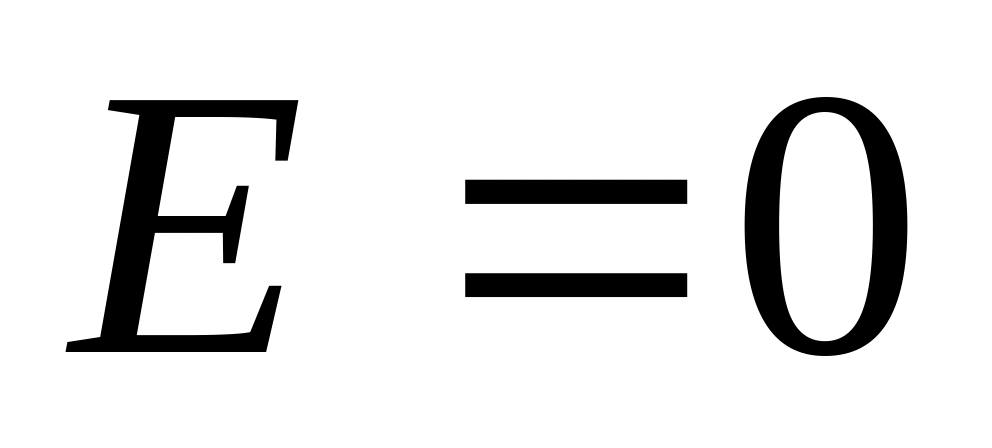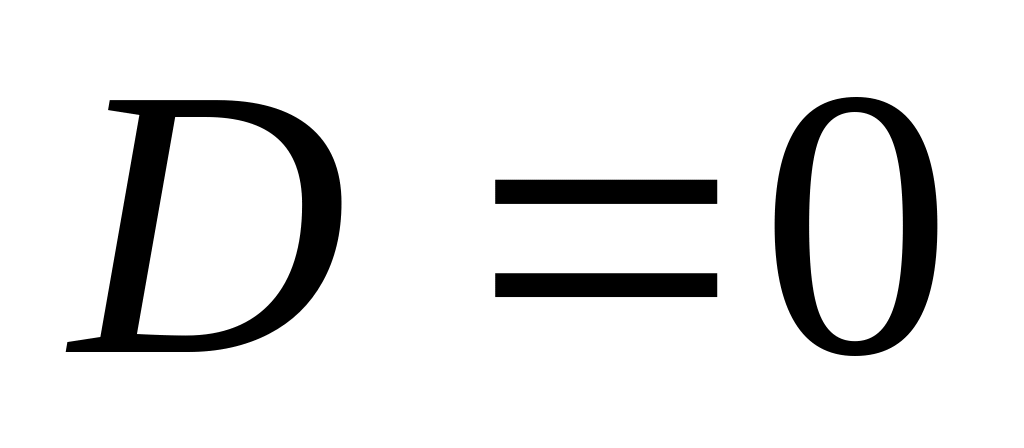• Найдем напряженность поля в пространстве между пластинами .

Выберем цилиндрическую гауссову поверхность, показанную на рис. 3 -штриховой линией. Образующие цилиндра параллельны оси , а основания параллельны заряженным плоскостям. Площадь каждого основания .

Левое основание находится в области , где , а правое проходит через точку поля с координатой , в которой вычисляется поле.

Поток смещения через поверхность цилиндра равен потоку только через правое основание:

.

Внутри гауссовой поверхности находится свободный заряд, размещенный на площадке левой плоскости и равный .

Тогда по теореме Гаусса ,

Отсюда .

В первом слое напряженность поля равна при .

Во втором слое при ,

г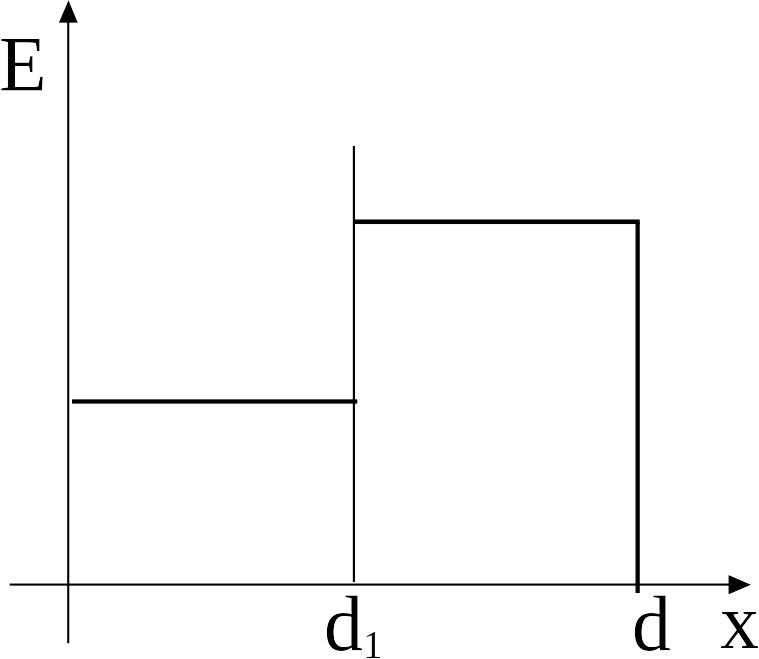 рафик зависимости при представлен на рис. 4.

3 . Поле равномерно заряженной сферы радиуса , окруженной концентрическими слоями двух разных диэлектрических сред.

Наружный радиус

- первой среды с относительной диэлектрической проницаемостью равен ,

- а второй среды равен (рис. 1).

За пределами второй среды - вакуум. Поверхностная плотность свободных зарядов на сфере радиуса равна .

Центр заряженной сферы и концентрических слоев диэлектриков является центром симметрии поля.

Поэтому в любой точке поля векторы и направлены радиально

• от центра , если ,

• или к центру , если , то есть ; .

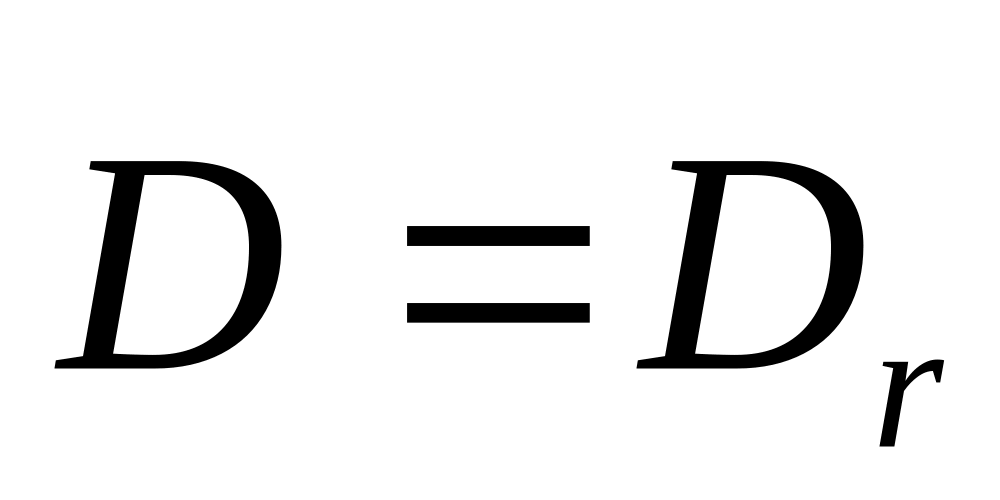Выберем в качестве гауссовой поверхности сферу с центром в точке и радиуса .

Во всех точках этой поверхности , где - проекция центра , в рассматриваемую точку поля на поверхности .

Из симметрии поля следует, что во всех точках поверхности значения одинаковы.

Поэтому поток смещения через поверхность равен:

С другой стороны, по теореме Гаусса, этот поток равен , причем

• , если

Таким образом, при ; и ,

• То есть при

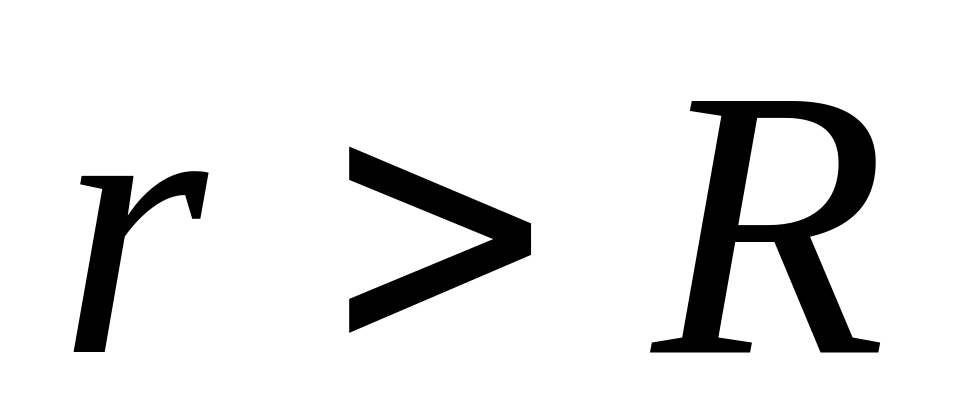
Для вектора имеем: .

Внутри сферы при ;

в первой среде при

во второй среде при ;

за пределами второй среды при .

Таким образом, терпит разрыв дважды:

1. на границе «первая и вторая среда»

2. и «вторая среда - вакуум».

Зависимость представлена на рис. 2.

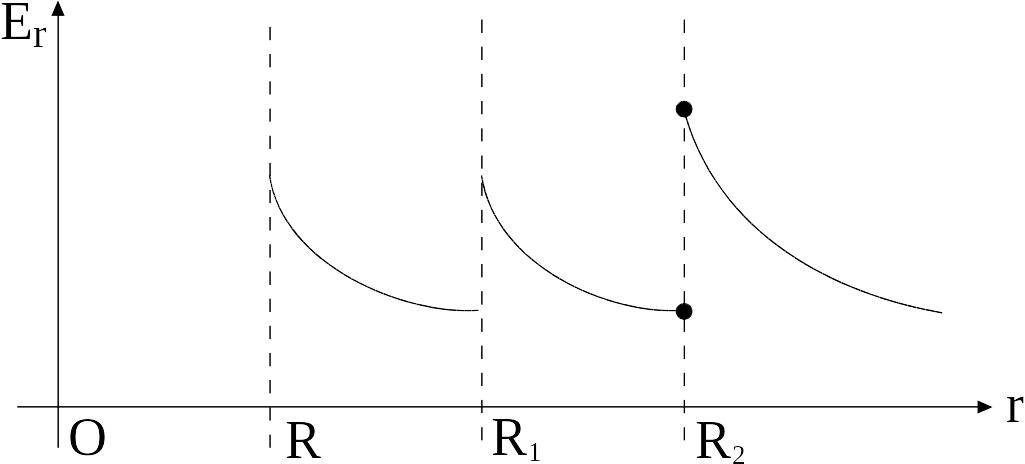
Р

4.

Поле внутри шарового слоя.

Окружим заряженную сферу концентрическим шаровым слоем из однородного диэлектрика.

• На внутренней поверхности слоя появится связанный заряд ; распределенный с плотностью ,

• на наружной поверхности заряд 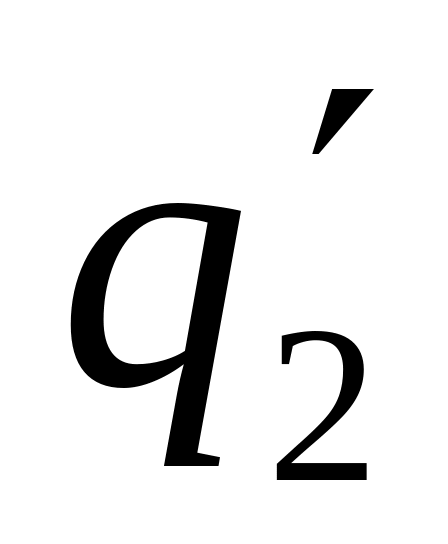, распределенный с плотностью 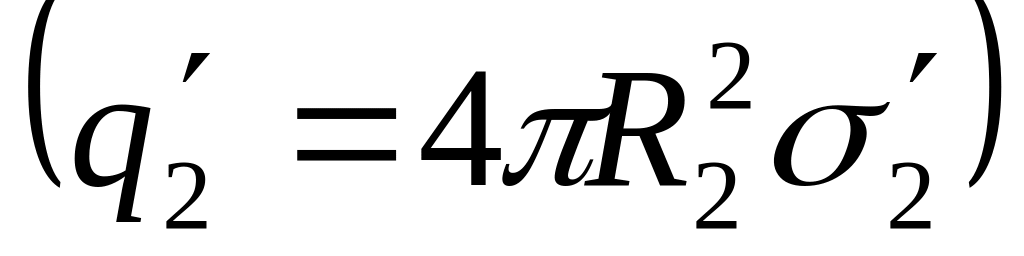. Знак заряда совпадает со знаком заряда сферы, знак ему противоположен

Напряженность поля внутри диэлектрика

и противоположна по направлению напряженности .

Результирующее поле -

поле убывает по закону .

Поэтому ,

где - напряженность поля в диэлектрике в непосредственной близости к внутренней поверхности слоя, именно эта напряженность определяет величину :

(в каждой точке поверхности ).

Тогда ,и ,

тогда .

Так как поле внутри диэлектрика изменяется по закону , то ,

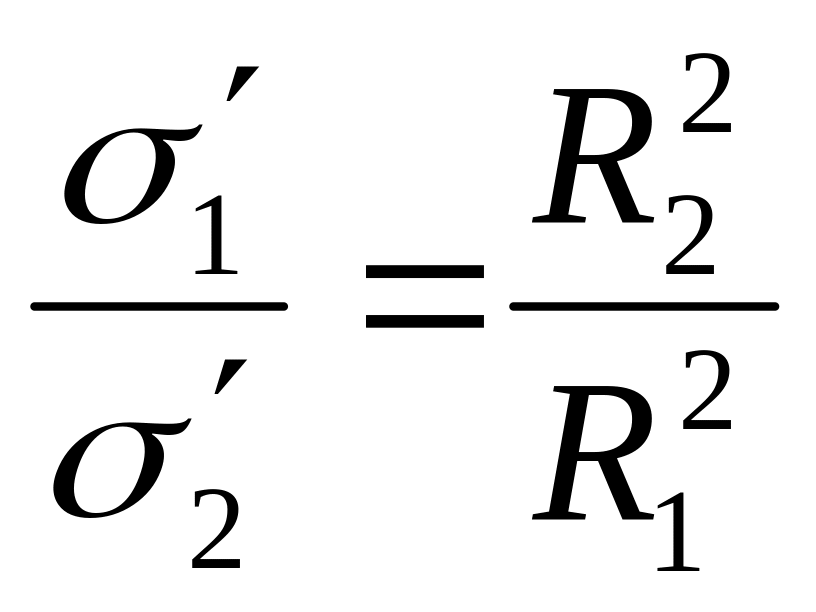тогда , или .

Следовательно, поля, создаваемые этими зарядами на расстояниях , взаимно уничтожают друг друга так что вне шарового слоя , .

Таким образом, однородный диэлектрик

полностью заполняет объем, ограниченный эквипотенциальными поверхностями, то вектор электрического смещения совпадает с вектором напряженности поля свободных зарядов, умноженным на , и напряженность поля внутри диэлектрика в раз меньше, чем напряженность поля свободных зарядов.