1.2.8.Условия на границе двух диэлектриков

М ожно показать, что линии смещения при переходе через границу диэлектриков не претерпевают разрыва.

Рис.2.7.

Поместим в однородное поле две сложенные вместе плоскопараллельные пластины из разных диэлектриков

- Сторонних зарядов на границе раздела нет.

- Возникшие на поверхностях пластин связанные заряды создают внутри каждой пластины перпендикулярное к ее поверхностям поле .

- В первой пластине напряженность этого поля равна ,

- во второй .

В сумме с нормальной составляющей напряженности поля свободных зарядов вектор дает нормальную составляющую результирующего поля в пластинах.

Векторы и коллинеарны, поэтому нормальные составляющие вектора напряженности в диэлектриках соответственно равны:

(2.15)

В направлении касательной к поверхности раздела никакого дополнительного поля не создается, поэтому тангенциальная составляющая вектора при переходе через границу не меняется:

. (2.16)

Поверхностная плотность связанных зарядов, как следует из выражения (2.6), определяется нормальной составляющей результирующего поля в данной пластине:

.

Подставив и в формулу (2.15), имеем (2.17)

Из выражений (2.16) и (2.17) следует, что при переходе через границу раздела двух диэлектриков

• нормальная составляющая напряженности поля изменяется скачком ( терпит разрыв),

• а тангенциальная составляющая остается без изменений.

Умножим выражения (2.16) и (2.17) на и соответственно, получаем

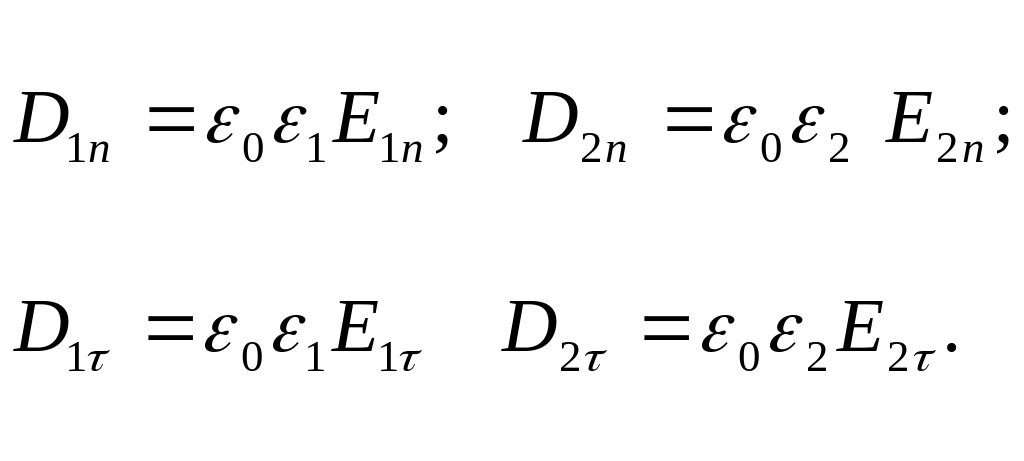(2.18)

Из формул (2.18) видно, что при переходе через границу раздела диэлектриков :

• тангенциальная составляющая вектора меняется скачком,

• а нормальная составляющая остается без изменений: (2.19)

Это равенство указывает на непрерывность линий смещения.

Действительно, количество линий электрического смещения, пронизывающих площадку , равно , следовательно, к площадке, расположенной на границе раздела диэлектриков, приходит из первого диэлектрика количество линий .

От этой же площадки уходит во второй диэлектрик количество линий .

Так как , то и .

Таким образом, линии электрического смещения не заканчиваются и не начинаются на границе раздела, т.е. проходят через нее, не претерпевая разрыва при условии, что на границе раздела нет сторонних зарядов.

Условие (2.19) справедливо и для границы диэлектрик-вакуум.

Рис. 2.8. На границе раздела диэлектриков линии вектора терпят излом (преломляются,

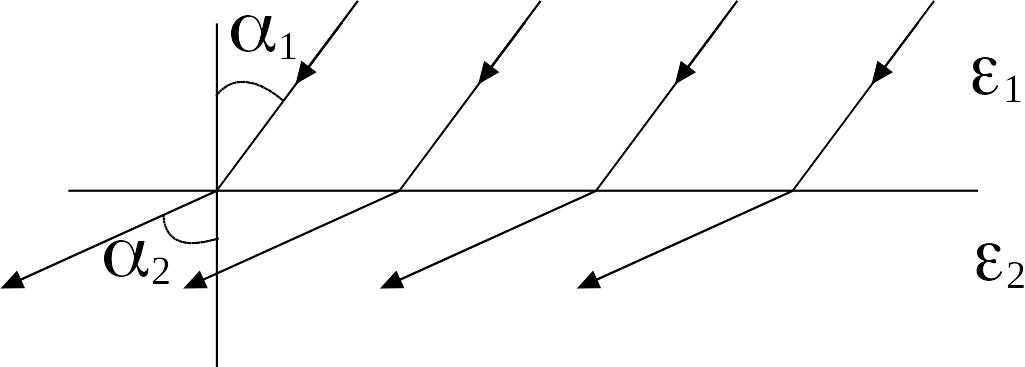, и угол между нормалью к поверхности раздела и линией изменяется:

получаем закон преломления линий электрического смещения:

.

При переходе в диэлектрик с меньшей ε угол уменьшается.

1.2.7. Примеры расчета электрических полей в диэлектриках

1. Поле внутри плоской пластины.

Пусть поле создано в вакууме двумя бесконечными разноименно заряженными плоскостями. Напряженность этого поля ; электрическое смещение .

Внесем в это поле пластину из однородного диэлектрика и расположим ее так, как показано на рис. 5.

Под действием поля диэлектрик поляризуется, и на его поверхностях появятся связанные заряды плотности .

Эти заряды создадут внутри пластины однородное поле, напряженность которого

.

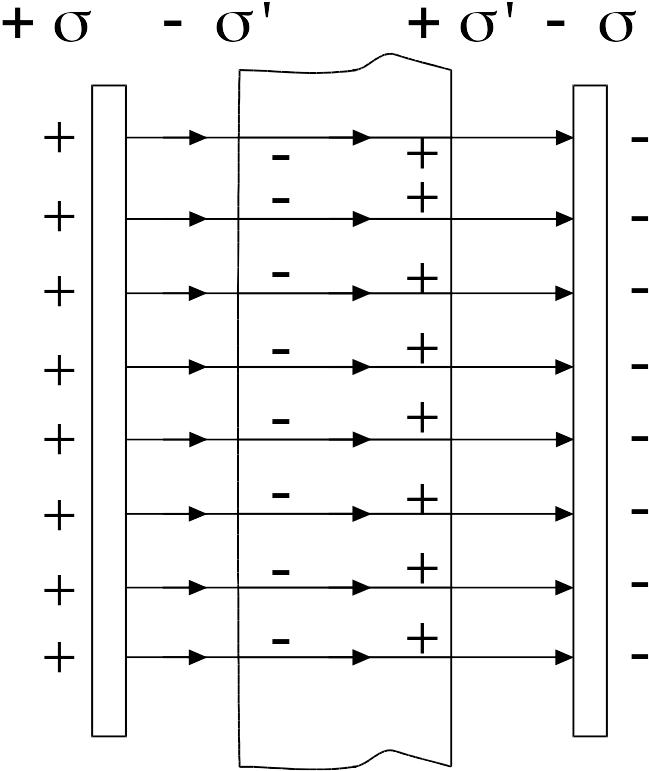Вне диэлектрика .

Напряженность поля .

Оба поля направлены навстречу друг другу, следовательно, внутри диэлектрика:

,

вне диэлектрика .

Поляризация диэлектрика обусловлена полем .

Оно перпендикулярно к поверхности пластины и ,

тогда , и , или

- то есть показывает, во сколько раз ослабляется поле за счет диэлектрика.

Умножим на , имеем

• - внутри пластины электрическое смещение равно напряженности поля свободных зарядов, умноженной на 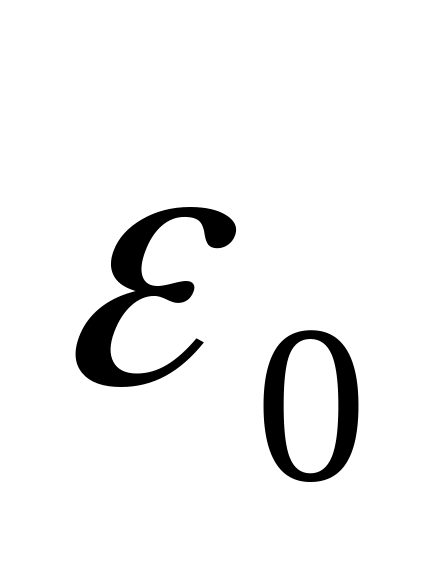, то есть совпадает с электрическим смещением внешнего поля .

• Вне пластины и .

Найдем :

и

, тогда .