1.2.5. Вектор электрического смещения
Источниками электрического поля служат не только сторонние, но и связанные заряды, т.е.
,
или
.
Раскрыв
скобки и сгруппировав, получаем:
(2.12)
Вектор
называют электрическим
смещением или электростатической
индукцией.
Подставим значения из выражения (2.4),
получаем
(2.13)
Безразмерная
величина
называется относительной
диэлектрической
проницаемостью
среды и характеризует электрические
свойства диэлектрика.
Для
всех диэлектриков
,
поэтому
.
Для
вакуума
и
,
поэтому
Таким образом, относительная диэлектрическая проницаемость среды показывает, во сколько раз поле в этой среде меньше, чем в вакууме.
Объединив
выражения (2.12) и (2.13), получаем теорему
Гаусса для вектора смещения
:
(2.14)
Дивергенция вектора электрического смещения равна объемной плотности сторонних зарядов.
Выражение
(2.14) проинтегрируем по
произвольному объему
V
Применив
теорему Остроградского, получаем
В правой части этого выражения стоит алгебраическая сумма зарядов, заключенных в объеме V,
а в левой - поток вектора через поверхность S, ограничивающую объем V.
Тогда
-
это интегральная
форма теоремы Гаусса для вектора
поток вектора электрического смещения через замкнутую поверхность равен алгебраической сумме сторонних зарядов, заключенных внутри этой поверхности.
Для графического представления электрического поля в диэлектрике неудобно пользоваться силовыми линиями (линиями напряженности), так как дивергенция вектора при наличии диэлектриков может быть отличной от нуля не только в точках расположения сторонних, но и в точках расположения связанных зарядов, плотность которых в свою очередь зависит от напряженности поля, неоднородностей среды, и т.д.
Поэтому для графического изображения поля в диэлектрике пользуются линиями электрического смещения, т.е. линиями вектора .
Вектор в каждой точке пространства ( за исключением анизотропных сред) параллелен вектору , поэтому каждая линия смещения является вместе с тем и силовой линией.
Линии смещения, так же как и силовые линии электростатического поля, не могут быть замкнутыми. Они начинаются или заканчиваются только на зарядах, или уходят в бесконечность.
Если строить линии поля так, чтобы густота линий , пересекающих площадку , была пропорциональна потоку вектора поля через эту площадку, то густота линий смещения и силовых линий будут меняться различным образом от одного участка пространства к другому.
Некоторые силовые линии будут обрываться на связанных отрицательных зарядах диэлектрика и начинаться на положительных , тогда как соответствующие линии смещения будут проходить через и за эти заряды до встречи со сторонними зарядами.
Из выражения (2.14) видно, что линии смещения могут начинаться и заканчиваться только на сторонних (свободных) зарядах, либо уходить в бесконечность.
В вакууме
,
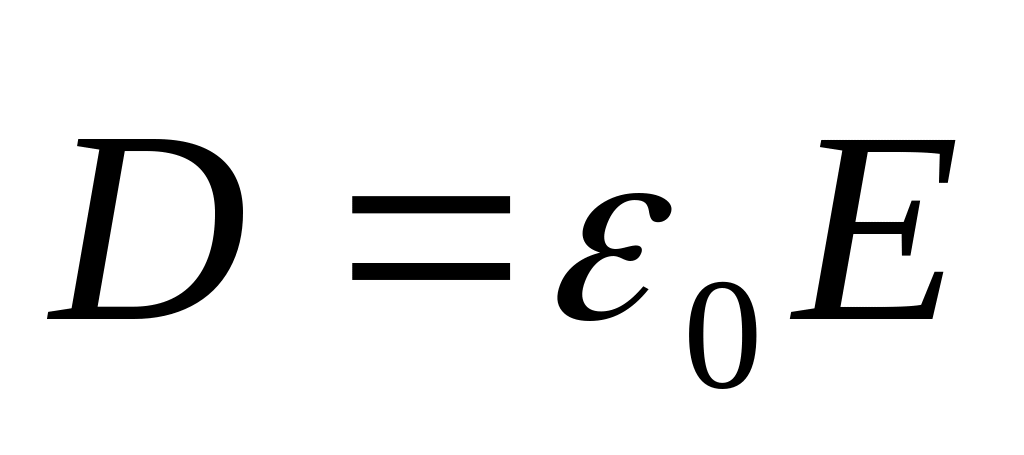и линии смещения совпадают с силовыми
линиями.