4.4. Потенциальная энергия во внешнем поле сил.

Из выражения (4.9) следует, что работа равна приращению потенциальной функции, и эта работа идет на приращение кинетической энергии частицы, как показывает (4.5).

Таким образом,

. (4.11)

Перейдем от функции к функции , связанной с соотношением

. (4.12)

Тогда из (4.11) получаем: , или .

Полученный результат означает, что величина для частицы, находящейся в поле консервативных сил, остается постоянной, т.е. является интегралом движения.

Функция называется потенциальной энергией частицы во внешнем поле сил.

Таким образом, потенциальная энергия

• характеризует взаимодействие частицы с полем сил

• зависит от положения частицы в этом поле, т.е. от координат.

Величину , равную сумме кинетической и потенциальной энергии, называют полной механической энергией частицы.

Из выражения (4.9) с учетом (4.12) получаем:

- работа, совершаемая над частицей силами консервативного поля, равна убыли потенциальной энергии частицы, т.е. работа совершается за счет запаса потенциальной энергии.

Выражение (4.7) с учетом (4.12) принимает вид:

– сила, действующая на частицу в стационарном поле сил, равна градиенту потенциальной энергии частицы в этом поле, взятому с обратным знаком.

Пусть на частицу, кроме сил стационарного потенциального поля, действует также неконсервативная сила .

Т огда при переходе частицы из точки 1 в точку 2 над ней будет совершаться работа ,где - работа неконсервативной силы.

Работа консервативных сил равна убыли потенциальной энергии. Тогда:

.

Суммарная работа всех приложенных к частице сил идет на приращение ее кинетической энергии:

, или

- работа неконсервативных сил затрачивается на приращение полной механической энергии частицы.

Потенциальная энергия, как и потенциальная функция, определяется с точностью до произвольной аддитивной постоянной. Однако, это не имеет значения, так как во все функции входит либо разность значений потенциальной энергии, либо ее производные. В каждой конкретной задаче выбирается начало отсчета потенциальной энергии, от которого ведут расчет энергии в других положениях. Поэтому может иметь как положительные, так и отрицательные значения.

Конкретный вид функции зависит от характера силового поля.

В поле тяжести , где отсчитывается от произвольного уровня.

Рассмотрим систему, состоящую из невзаимодействующих между собой частиц, находящихся в поле консервативных сил.

Каждая из частиц обладает кинетической и потенциальной энергией номер частицы, тогда для каждой частицы можно записать:

Просуммировав эти выражения для всех частиц, получаем:

- полная механическая энергия системы невзаимодействующих частиц, на которые действуют только консервативные силы, остается постоянной.

4.5. Потенциальная энергия взаимодействия.

Рассмотрим замкнутую систему, состоящую из двух взаимодействующих частиц (рис.4.7).

В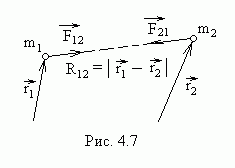 ведем вектор , где и - радиус-векторы частиц. Расстояние между частицами равно модулю этого вектора.

Будем считать, что силы взаимодействия частиц и зависят только от расстояния между ними, и направлены вдоль прямой, соединяющей частицы:

, (4.13)

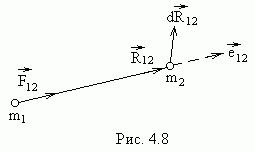г де - некоторая функция , - орт вектора (рис.4.8).

По третьему закону Ньютона =  .

Уравнения движения частиц .

Умножим первое уравнение на , второе – на и сложим:

. (4.14)

Левая часть этого выражения представляет собой приращение кинетической энергии системы за время , а правая часть – работу внутренних сил за то же время:

.

Подставив в это выражение формулу (4.13), получаем .

Из рис.4.7 видно, что скалярное произведение равно приращению расстояния между частицами.

Тогда .

Выражение есть приращение некоторой функции от :

.

Следовательно, и выражение (4.14) можно представить в виде:

.

или таким образом, величина для замкнутой системы сохраняется.

Функция представляет собой потенциальную энергию взаимодействия. Она

• зависит от расстояния между частицами.

• р абота внутренних сил

Т.е. не зависит от путей, по которым перемещались частицы, а определяется только начальными и конечными расстояниями между частицами.

Таким образом, силы взаимодействия вида (4.13) являются консервативными.