МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Государственное образовательное учреждение высшего профессионального образования

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПРИКЛАДНОЙ БИОТЕХНОЛОГИИ (МГУПБ)

Кафедра технологического оборудования и процессов отрасли

ОСНОВЫ МЕХАТРОНИКИ

А.Я. Красинский, Д.Р. Каюмова, А.А. Халиков

ОДНОРОДНЫЕ ПРЕОБРАЗОВАНИЯ

Методические указания к самостоятельной работе

для студентов специальностей

220401 – Мехатроника

260601 – Машины и аппараты пищевых производств

260602 – Пищевая инженерия малых предприятий

и направления подготовки уровня бакалавриата 150400 – Технологические машины и оборудование

Москва 2010

Составители: А.Я. Красинский, д.ф.-м.н., проф.

А.А. Халиков, асп.

Д.Р. Каюмова, асп.

Методические указания составлены в соответствии с рабочей программой по курсу «Основы мехатроники». Цель методических указаний – ознакомление студентов с однородными преобразованиями и приобретение навыков составления матриц однородных преобразований.

Предназначены для студентов специальностей 220401 – Мехатроника, 260601 – Машины и аппараты пищевых производств, 260602 – Пищевая инженерия малых предприятий и направления подготовки уровня бакалавриата 150400 – Технологические машины и оборудование.

Утверждены УМС МГУПБ.

© МГУПБ, 2011

Введение

Одним из важных классов роботов является класс манипуляционных роботов. Манипуляционные роботы в ходе работы постоянно выполняют операции позиционирования (перемещение) и ориентирования (вращение) кисти робота (схвата). Кинематика таких движений может быть описана перемещением и вращением систем координат, связанных с частями конструкции манипуляционного робота.

С точки зрения кинематики манипуляционный робот представляет собой незамкнутую цепь звеньев, соединенных последовательно поступательными или вращательными сочленениями. Один конец манипулятора робота обычно закреплен, а второй соединен с рабочим орудием. Цель управления таким роботом – поместить схват в определенную точку с определенной ориентацией в заданное время.

Положение и ориентация схвата манипуляционного робота могут быть описаны через положение и ориентацию системы координат, связанной со схватом, по отношению к инерциальной базовой системе координат.

Совокупность положения и ориентации схвата в пространстве (кинематическое положение) математически может быть описана при помощи однородных преобразований размерности 4х4. Эти однородные преобразования могут использоваться при решении прямой и обратной кинематических задач. Кинематическое положение схвата обычно выражается матрицей размера 4х4, в которую входит вектор р положения начала системы координат схвата, а также матрица вращения R размером 3х3.

Система координат А представляется однородным преобразованием размера 4х4, которое описывает положение ее начала координат и поворот по отношению к базовой инерциальной системе координат. Однородное преобразование определяется как матрица H размера 4х4, которая в общем случае описывает перенос, вращение, растяжение (масштабирование) и перспективную проекцию векторов, точек, тел и других видов объектов. В общем случае она состоит из матрицы вращения R 3х3, матрицы переноса p 3х1, вектора перспективной проекции b 1х3 и матрицы масштабирования (растяжения) w 1х1:

. (1)

Манипулятор состоит из набора звеньев, соединенных при помощи сочленений. Однородные преобразования по отношению к локальным системам координат сочленений называются А-матрицами (т.е. преобразования Денавита-Хартенберга). Пусть А₁ описывает положение и ориентацию первого звена, А₂ – второго и т.д. в системе координат основания. Тогда положение и ориентация n-го звена в системе координат основания будут:

(2)

Данная формула справедлива и в том случае, если A_i – матрица, описывающая ориентацию и положение i-го звена в системе координат (i – 1)-го звена, а не в системе координат основания.

1. Ход работы

Ниже будет рассмотрен пример нахождения матрицы сложного однородного преобразования, описывающего последовательность вращений и переносов.

Для нахождения матрицы сложного однородного преобразования необходимо найти матрицы простых однородных преобразований и последовательно перемножить их.

Нахождение матрицы простых однородных преобразований размера 4х4 сводится к вычислению косинусов углов между осями (матрица вращения размера 3х3) и заполнению матрицы переноса (размера 3х1), входящую в состав матрицы преобразования.

2. Пример

Найдем выражение для матрицы сложного однородного преобразования, которое получим последовательным выполнением следующих преобразований:

1. вращение на угол (ψ+90°) относительно оси x;

2. перенос на a единиц вдоль оси у;

3. перенос на b единиц вдоль оси z;

4. вращение на угол –θ относительно оси y;

5. вращение на угол –φ относительно оси z.

1. На рис. 1 показано вращение относительно оси x.

Рис. 1

С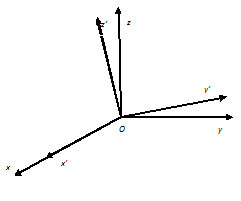 оставим выражение для матрицы A₁ вращения на угол (ψ+90°) относительно оси x:

Первые три строки и столбца матрицы A₁ представляют собой матрицу вращения – косинусы углов между осями глобальной (инерционной) и локальной (преобразованной) системы координат. Столбцы матрицы вращения соответствуют осям локальной системы координат x’, y’ и z’ соответственно, строки матрицы вращения – осям глобальной системы координат x, y и z соответственно. Поскольку масштабирование, перенос и перспективная проекция не производятся, элемент, стоящий на пересечении 4-й строки и 4-го столбца равен единице, а оставшиеся элементы 4-й строки и 4-го столбца равны нулю.

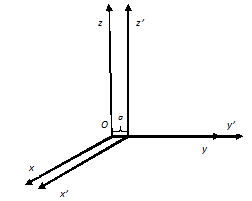
2. На рис. 2 показан перенос на a единиц вдоль оси у.

Составим выражение для матрицы A₂ данного преобразования:

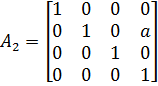Матрица вращения является единичной, поскольку вращение не происходит. Второй элемент четвертого столбца равен a, поскольку перенос происходит вдоль оси y.

Рис. 2

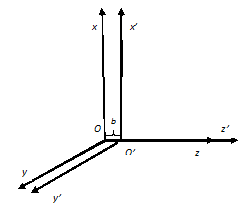
3. Н а рис. 3 показан перенос на b единиц вдоль оси z.

Составим выражение для матрицы A₃ данного преобразования:

Матрица вращения является единичной, поскольку вращение осей локальной системы координат относительно осей глобальной системы не происходит. Третий элемент четвертого столбца равен b, поскольку перенос Рис. 3 происходит вдоль оси z.

4. На рис. 4 показано вращение относительно оси y.

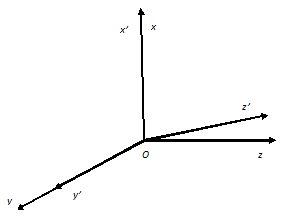
Составим выражение для матрицы A₄ вращения на угол –θ относительно оси y:

Рис. 4

5. Н 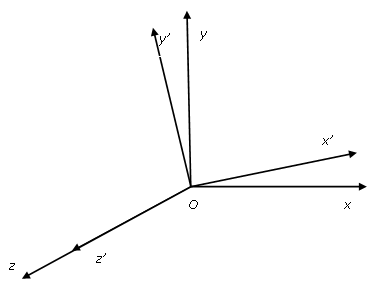а рис. 5 показано вращение относительно оси z.

Составим выражение для матрицы A₅ вращения на угол –φ относительно оси z:

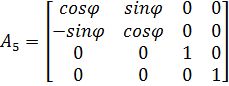
Рис. 5

6. Получим выражение для матрицы сложного однородного преобразования, используя (2):

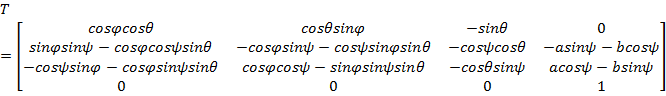
Некоторые вычисления, необходимые для решения обсуждаемой в этой работе задачи, например, умножение матриц, можно провести на компьютере, например, с использованием языка языка Python¹ [3] и библиотеки SymPy².

Для работы необходимо запустить программу IDLE³. Когда Python установлен в Windows, его можно найти в меню Пуск (Start). Набор пунктов меню может немного отличаться в зависимости от версии, но пункт IDLE запускает среду разработки с графическим интерфейсом, а пункт Python запускает сеанс работы с интерактивной командной оболочкой (консолью). Кроме того, здесь можно увидеть пункты вызова стандартного справочного руководства - Python Manuals.

Чтобы использовать функции SymPy нужно импортировать соответствующую библиотеку, выполнив команду:

>>> from sympy import *

Определим символы l₁, l₂, q₁, q₂ , чтобы использовать их при записи элементов матрицы J:

>>> psi = Symbol('psi') >>> a = Symbol('a') >>> b = Symbol('b') >>> theta = Symbol('theta') >>> phi = Symbol('phi')

Введем матрицы A_i в компьютер:

>>> A1=Matrix([[1,0,0,0],[0,-sin(psi),-cos(psi), 0],[0,cos(psi),-sin(psi),0],[0,0,0,1]]) >>> A2=Matrix([[1,0,0,0],[0,1,0,a],[0,0,1,0],[0,0,0,1]]) >>> A3=Matrix([[1,0,0,0],[0,1,0,0],[0,0,1,b],[0,0,0,1]]) >>> A4=Matrix([[cos(theta),0,-sin(theta),0],[0,1,0,0],[sin(theta),0,cos(theta),0],[0,0,0,1]]) >>> A5=Matrix([[cos(phi),sin(phi),0,0],[-sin(phi),cos(phi),0,0],[0,0,1,0],[0,0,0,1]])

Выведем произведение матриц A_i – матрицу сложного однородного преобразования:

>>> print A1*A2*A3*A4*A5