1.4.3.Энергия поляризованного диэлектрика

Рассмотрим однородный изотропный диэлектрик, находящийся во внешнем электрическом поле.

Происходит процесс поляризации как электронной, так и ориентационной.

Этот процесс связан с работой по деформации электронных орбит в атомах и молекулах и по повороту осей молекул-диполей вдоль поля. Ясно, что поляризованный диэлектрик должен обладать запасом электрической энергии.

Если поле напряженностью создано в вакууме, ,

то объемная плотность энергии этого поля в точке с напряженностью равна:

Докажем, что объемная плотность энергии поляризованного диэлектрика в этой точке выражается формулой: .

Рассмотрим диэлектрик с неполярными молекулами.

Молекулы такого диэлектрика являются упругими диполями.

Электрический момент упругого диполя, находящегося в поле с напряженностью , равен:

, где - поляризуемость диполя.

Или в скалярной форме: (1)

- заряд и плечо диполя.

На заряд со стороны поля действует сила ,

которая при увеличении длины диполя на совершает работу .

Из выражения (1) получаем: ,

поэтому . (2)

Чтобы найти работу поля при деформации одного упругого диполя, надо проинтегрировать выражение (2):

.

Работа равна той потенциальной энергии, которой обладает упругий диполь в электрическом поле напряженностью .

Пусть - число диполей в единице объема диэлектрика.

Тогда потенциальная энергия всех этих диполей, то есть объемная плотность энергии поляризованного диэлектрика равна: .

Однако - модуль вектора поляризации, тогда .

Известно, что , и ,

Тогда , что и требовалось доказать.

1.4.4. Закон сохранения энергии для электрического поля в несегнетоэлектрической среде

Энергия электрического поля, создаваемого какой-либо системой заряженных тел (проводников, диэлектриков), изменяется, если тела системы перемещаются (то есть меняется взаимное положение тел), или, если изменяются их заряды.

При этом совершают работу внешние силы, приложенные к телам системы, и источники электрической энергии (батареи, генераторы, и тому подобные), присоединенные к проводникам системы.

Закон сохранения энергии для малого изменения состояния системы при постоянной температуре и постоянной плотности среды имеет вид: .

Здесь:

• - работа внешних сил;

• - изменение энергии электростатического поля системы;

• - изменение кинетической энергии системы;

• - теплота Джоуля - Ленца, которая вызвана прохождением электрических токов в системе при изменении или перераспределении зарядов проводников.

Если перемещение тел производится квазистатически, то есть очень медленно, то можно

• пренебречь изменением кинетической энергии системы,

• и считать работу внешних сил численно равной и противоположной по знаку работе , совершаемой в рассматриваемом процессе силами, которые действуют на тела системы в электрическом поле и называются пондемоторными силами.

В этом случае закон сохранения энергии можно записать в виде: .

Работа источников электрической энергии за малый промежуток времени равна:

,

где - общее число источников электрической энергии в рассматриваемой системе;

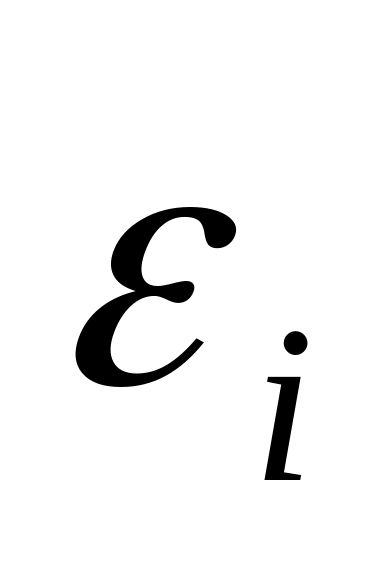• - ЭДС -того источника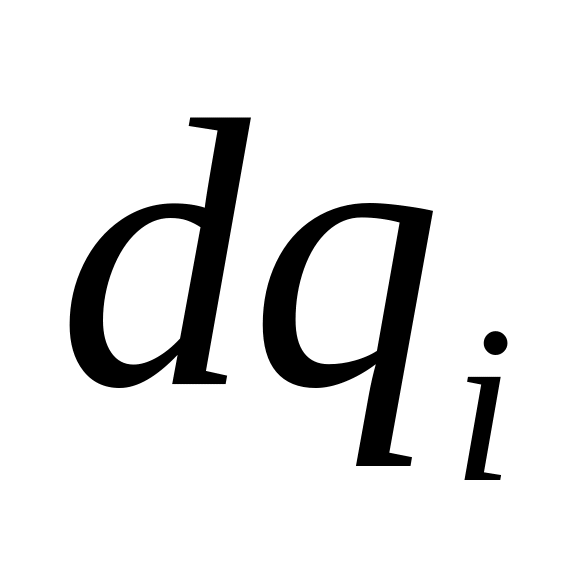

• - заряд, проходящий через этот источник за время , - ток в источнике

• работа , если ток идет от катода к аноду.

Если заряд каждого проводника не изменяется и не перераспределяется, то выражение закона сохранения энергии для квазистатического изменения состояния системы имеет вид:

,

то есть в этом процессе работа пондемоторных сил равна убыли энергии электрического поля системы. С помощью этого выражения можно рассчитывать работу пондемоторных сил.

Пример. Найдем силы, действующие на пластины заряженного плоского конденсатора. Расстояние между пластинами , где - площадь пластины.

Конденсатор заряжен и отключен от источника питания, так что заряд конденсатора , - поверхностная плотность заряда.

При увеличении расстояния сила , приложенная к перемещаемой пластине, совершает работу .

Изменение энергии электростатического поля в конденсаторе , где - объемная плотность энергии в прилегающем к пластине слое толщиной .

Таким образом, из закона сохранения энергии следует, что конденсаторная сила равна .

Возможны два случая:

1. Конденсатор с газообразным или жидким диэлектриком между пластинами.

В этом случае все пространство между пластинами конденсатора независимо от величины расстояния между ними заполнено одним и тем же диэлектриком с относительной диэлектрической проницаемостью , тогда

;

, где - пондемоторная сила, действующая в вакууме.

2. Конденсатор с твердым диэлектриком между пластинами.

В этом случае в слое толщиной , образовавшемся в результате отодвигания пластины конденсатора находится воздух, относительная диэлектрическая проницаемость которого .

Поэтому ; .

Решим задачу на определение работы и энергии электростатического поля.

1. Предположим, что радиус электрона равен радиусу протона, , и заряд электрона сосредоточен на его поверхности.

1. Какова потенциальная энергия системы?

2. Какой релятивистской массе соответствует эта энергия.

Решение:

Эквивалентная ей масса равна:

(Экспериментально , так как )

11