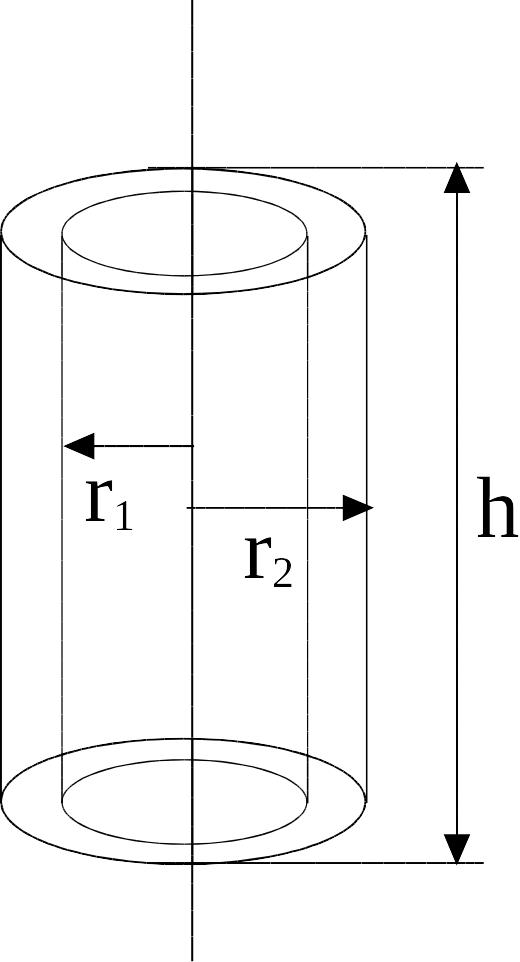
3. Цилиндрический конденсатор

• состоит из двух полых коаксиальных металлических цилиндров с радиусами и , вставленных один в другой.

• Заряды на обкладках и ,

• высота цилиндра ; .

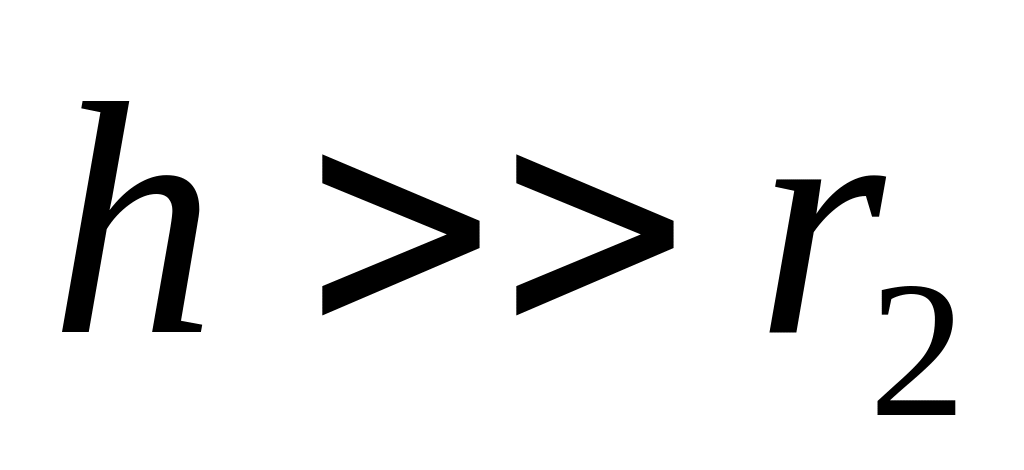• В этом случае можно вычислять разность потенциалов между обкладками по формуле для поля, создаваемого бесконечно длинным прямым цилиндром радиуса , равномерно заряженным с постоянной линейной плотностью : ,

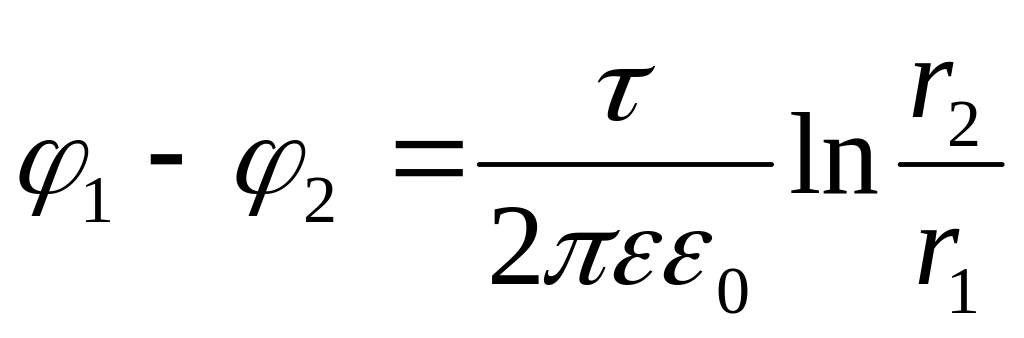• Тогда

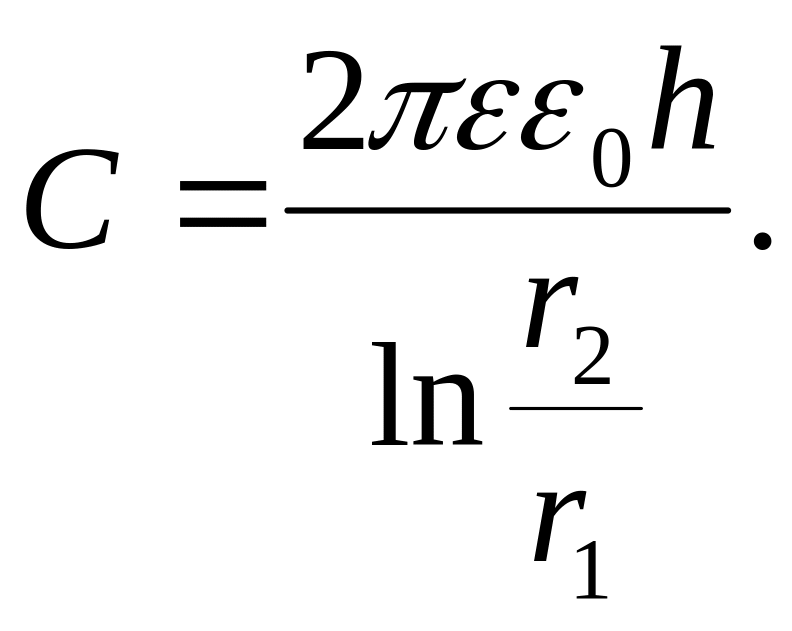
Пример цилиндрического конденсатора – лейденская банка.

Если зазор между обкладками конденсатора мал , то

и , где - боковая площадь обкладки.

Таким образом, электроемкость любого конденсатора пропорциональна диэлектрической проницаемости вещества, заполняющего зазор между обкладками.

Кроме электроемкости конденсатор характеризуется пробивным напряжением. Это разность потенциалов между обкладками, при которой может произойти пробой.

1.3.5. Соединения конденсаторов

1. П 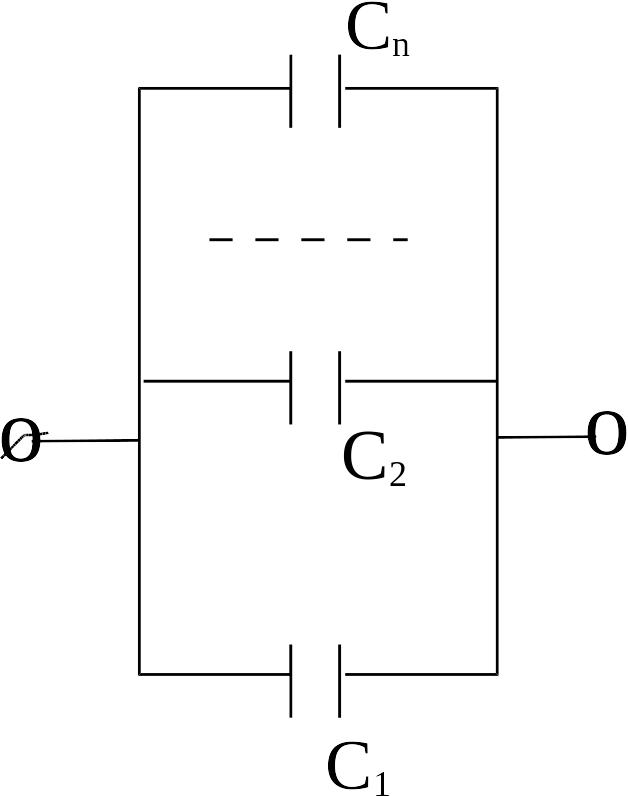араллельное соединение.

• Емкости конденсаторов соответственно равны .

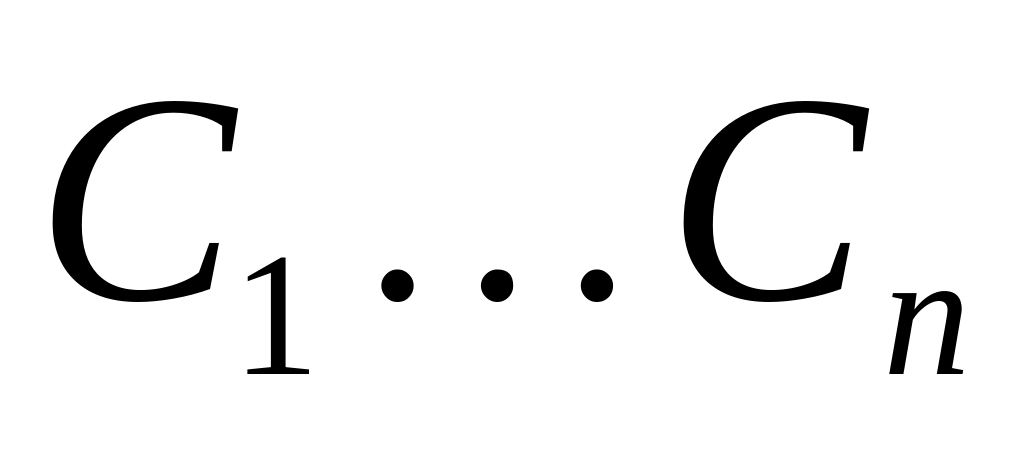• Разности потенциалов для всех конденсаторов одинаковы,

• поэтому заряды

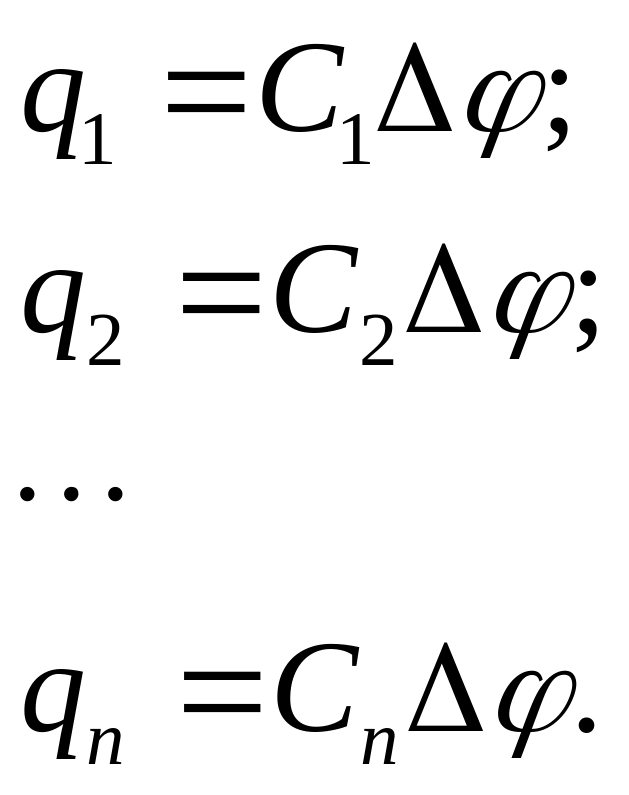
• Заряд всей батареи

.

Но, с другой стороны , тогда

2. Последовательное соединение.

• В этом случае

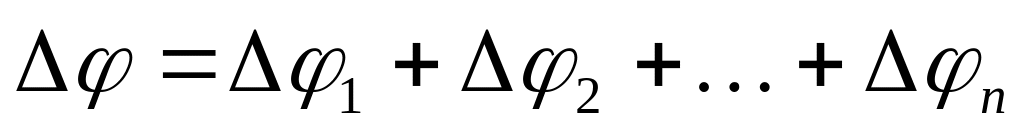
• (заряды всех пластин одинаковы)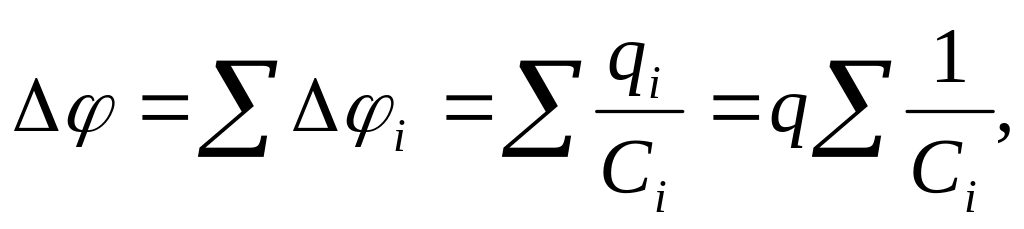

• 

• отсюда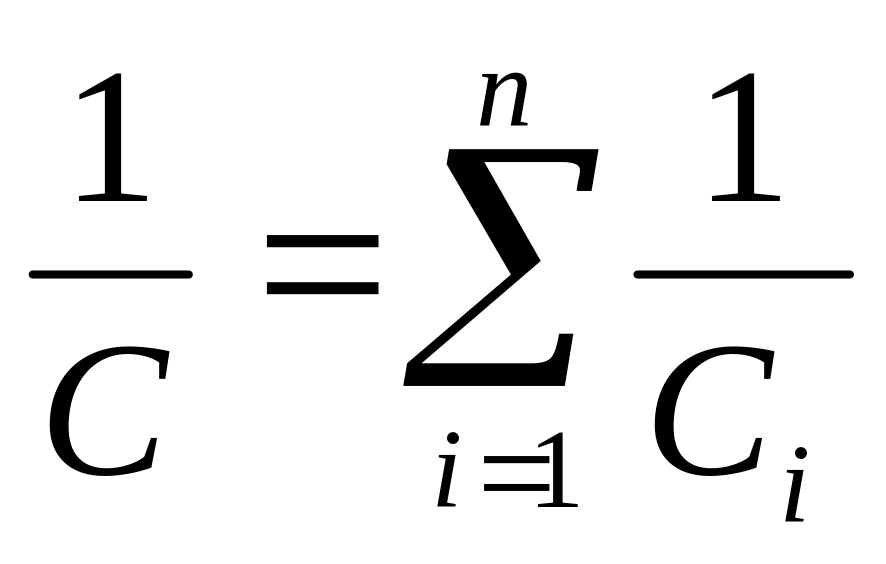 - при последовательном соединении конденсаторов величина, обратная общей электроемкости, равна сумме величин, обратных электроемкостям отдельных конденсаторов.

• То есть результирующая электроемкость всегда меньше минимальной электроемкости, входящей в батарею.

Лекция14/ 7

1.4.Энергия электрического поля

1.4.1.Энергия заряженного проводника

Будем считать среду, в которой находятся электрические заряды и заряженные тела, однородной и изотропной, не обладающей сегнетоэлектрическими свойствами.

Заряжая некоторый проводник, необходимо совершить определенную работу против кулоновских сил отталкивания между одноименными электрическими зарядами.

Эта работа идет на увеличение электрической энергии заряженного проводника, которая в данном случае аналогична потенциальной энергии в механике.

Рассмотрим проводник, имеющий

• электроемкость ,

• заряд

• и потенциал .

Работа, совершаемая против сил электростатического поля при перенесении заряда из бесконечности на проводник равна .

Для того, чтобы зарядить тело от нулевого потенциала до потенциала , необходимо совершить работу .

Ясно, что энергия заряженного тела равна той работе, которую нужно совершить, чтобы зарядить это тело:

.

Энергию называют собственной энергией заряженного тела.

Ясно, что собственная энергия есть не что иное, как энергия электростатического поля этого тела

1.4.2.Энергия заряженного конденсатора

Пусть

• потенциал обкладки конденсатора, на которой находится заряд , равен

• а потенциал обкладки, на которой находится заряд , .

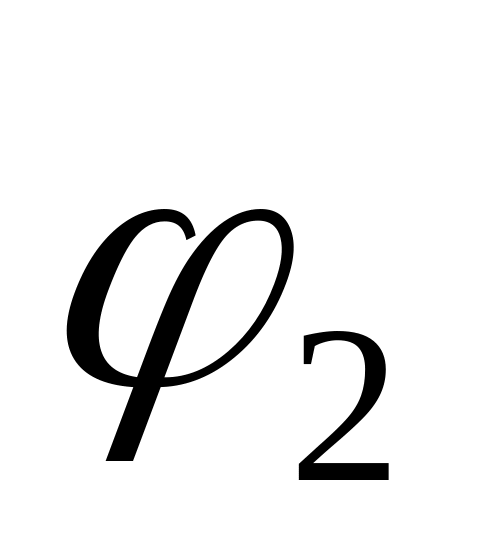Энергия такой системы зарядов равна:

,

то есть равна собственной энергии системы зарядов,

где - напряжение между обкладками конденсатора, .

Найдем энергию

1. плоского конденсатора.

Энергия, заключенная в единице объема электростатического поля называется объемной плоскостью энергии.

Эта объемная плоскость должна быть одинаковой во всех точках однородного поля, а полная энергия поля пропорциональна его объему.

Известно, что , ,

тогда для энергии имеем: ,

но - объем электростатического поля между обкладками конденсатора,

то есть .

Тогда объемная плотность энергии однородного электростатического поля конденсатора равна ,

то есть определяется его напряженностью или смещением.

В случае неоднородных электрических полей .

2. сферического конденсатора.

На расстоянии от центра заряженного шара напряженность его электростатического поля равна .

Рассмотрим бесконечно тонкий шаровой слой, заключенный между сферами радиусов и .

Объем такого слоя: .

Энергия слоя ,

следовательно .

Тогда полная энергия заряженного шара равна: , где - радиус шара.

Но емкость шара ,

следовательно, - энергия электростатического поля сферического конденсатора равна его собственной энергии, так как заряженное тело потому и обладает электрической энергией, что при его зарядке была совершена работа против сил создаваемого им электростатического поля.