1.3.4. Взаимная электроемкость. Конденсаторы

Рассмотрим проводник , вблизи которого имеются другие проводники.

Этот проводник уже нельзя считать уединенным, его емкость окажется большей, чем емкость уединенного проводника.

Это связано с тем, что при сообщении проводнику заряда окружающие его проводники заряжаются через влияние, причем ближайшими к наводящему заряду оказываются заряды противоположного знака. Эти заряды несколько ослабляют поле, создаваемое зарядом . Таким образом, они понижают потенциал проводника и повышают его электроемкость.

Р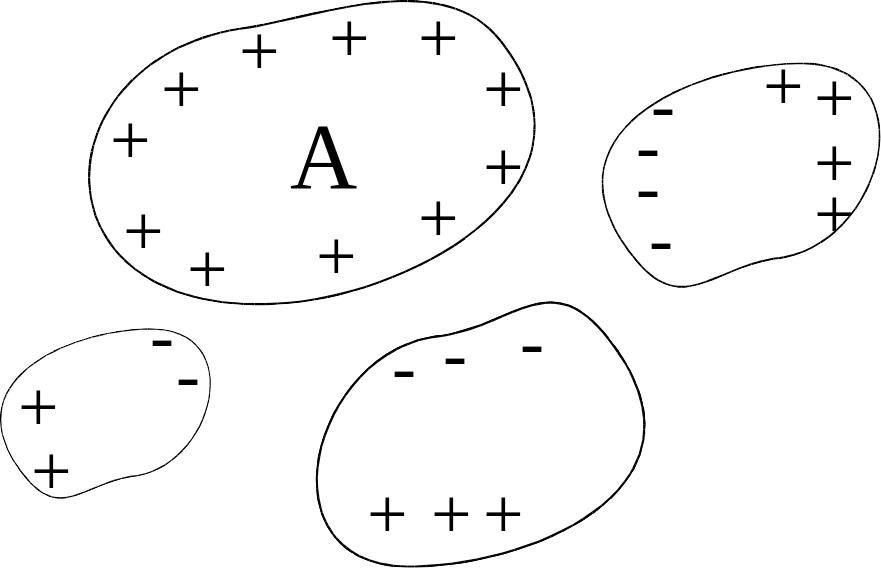 ассмотрим систему, составленную из близко расположенных проводников, заряды которых численно равны, но противоположны по знаку.

Обозначим разность потенциалов между проводниками ,

абсолютная величина зарядов равна .

Если проводники находятся вдали от других заряженных тел, то ,

где - взаимная электроемкость двух проводников:

она численно равна заряду, который необходимо перенести с одного проводника на другой для изменения разности потенциалов между ними на единицу.
зависит от их формы, размеров и взаимного расположения, а также от диэлектрической проницаемости среды.

Для однородной среды .

Если один из проводников удалить, то разность потенциалов возрастает, и взаимная емкость убывает, стремясь к значению емкости уединенного проводника.

Рассмотрим два разноименно заряженных проводника, у которых форма и взаимное расположение таковы, что создаваемое ими поле сосредоточено в ограниченной области пространства. Такая система называется конденсатором.

Плоский конденсатор

имеет две параллельные металлические пластины площадью , расположенные на расстоянии одна от другой.
Заряды пластин и .
Если линейные размеры пластин велики по сравнению с расстоянием , то электростатическое поле между пластинами можно считать эквивалентным полю между двумя бесконечными плоскостями, заряженными разноименно с поверхностными плотностями зарядов 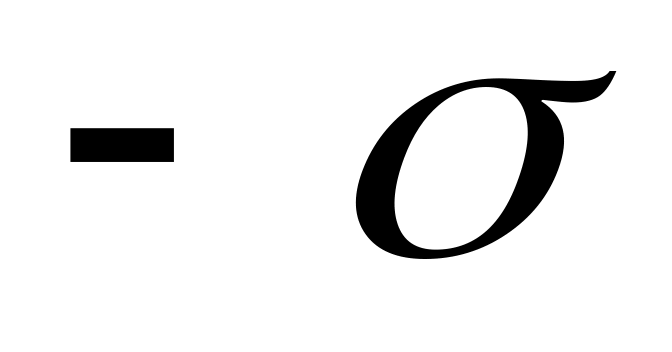и ,
напряженность поля ,
разность потенциалов между обкладками ,
тогда ,

де - диэлектрическая проницаемость среды, заполняющей конденсатор.

Сферический конденсатор

состоит из металлического шара радиусом , окруженного концентрическим с ним полым металлическим шаром радиусом , .
Вне конденсатора поля, создаваемые внутренней и внешними обкладками, взаимно уничтожаются.
Поле между обкладками создается только зарядом шара , так как заряд шара не создает внутри этого шара электрического поля.
Поэтому разность потенциалов между обкладками: ,
Тогда