МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Технологический институт

Федерального государственного образовательного учреждения

высшего профессионального образования

«Южный федеральный университет»

ПРИОРИТЕТНЫЙ НАЦИОНАЛЬНЫЙ ПРОЕКТ «ОБРАЗОВАНИЕ»

В.А. Костюков

ЭЛЕКТРОТЕХНИКА

Учебное пособие

Часть 4

Таганрог 2007

Содержание

1. Основные понятия электротехники

2. Гармонический режим работы цепи

2.1. Основные правила работы с комплексными числами

2.2. Метод комплексных амплитуд. Законы Кирхгофа в частотной области

2.3. Баланс мощности для гармонической цепи

2.4 Метод эквивалентных преобразований для синусоидальных цепей.

Задачи по пунктам 2.1. – 2.4.

2.5. Резонансные явления в колебательных контурах с источниками гармонического сигнала

3. Методы анализа сложных цепей при гармоническом воздействии

3.1. Метод контурных токов

3.2. Метод узловых напряжений

4. Переходные процессы в цепях с сосредоточенными параметрами

5. Обеспечение электробезопасности

5.1 Технические средства электрозащиты

5.2.Организационные средства электрозащиты

Приложение 1. Расчет отклика линейной цепи на сложное воздействие

1. Основные понятия электротехники

В предыдущем методическом руководстве “Электротехника и практика” мы бегло рассмотрели некоторые электротехнические устройства, затронув практический аспект электротехники. Вместе с тем было отмечено, что получить столь впечатляющих результатов в области разработки и внедрения этих устройств было бы невозможно без соответствующей теоретической базы. Причем, как выяснилось, знания основных законов электротехники, знакомые вам еще из школы, могут помочь практически (см. примеры по выбору плавких предохранителей и задачу о возникновении перегрузки квартирной сети). Однако для решения более сложных задач, которые, несомненно, могут встретиться вам, например, при прокладке электросети в доме, при использовании электродвигателей, при ремонте электрооборудования или при установке заземляющих устройств (или даже просто при ознакомлении с паспортом нового холодильника, стиральной машины, счетчика, генератора и т.д.), необходимы более глубокие знания.

Поэтому в этом разделе мы кратко рассмотрим основания электротехники, т.е. научный базис, на котором строятся основные ее понятия, такие как электрический ток, напряжение, сопротивление, проводимость, емкость, индуктивность и др.

Все электротехнические термины и законы есть результат применения строгих электродинамических представлений, основанных на уравнениях Максвелла и материальных уравнениях среды, в которой происходят электромагнитные явления.

Джемс Клерк Максвелл (1831-1879), базируясь на глубоких идеях М. Фарадея (закон электромагнитной индукции, понятие об электрических и магнитных силовых линиях как реальных образованиях в пространстве), в своих коротких уравнениях заложил фундамент теоретической электродинамики. Одним из следствий уравнений Максвелла явилось предсказание существования электромагнитных волн. Им же обоснована электромагнитная природа света.

Для вывода своих уравнений Максвелл использовал аналогию между свойствами несжимаемой жидкости и электромагнитных процессов. Средой, в которой по Максвеллу распространяется электромагнитная волна, является эфир. Хотя гипотеза о существовании эфира и была отклонена в теории относительности Эйнштейна, современные теории заставляют более серьезно рассмотреть возможность существования такой “абсолютной” среды (для примера укажем теорию физического вакуума, который возможно и есть гипотетический эфир).

Касаясь фундамента электродинамики, еще отметим, что в настоящее время поле (в том числе электромагнитное) рассматривается как один из видов материи (наряду с веществом). Но, как писал Эйнштейн, не исключено, что в будущем наука придет к единой теории поля, которая сможет вещество представить как полевую структуру. Тогда был бы вскрыт фундамент всей материи, и любой ее вид объяснялся как порождение одного и того же.

Сейчас же мы займемся разъяснением основных понятий электротехники.

Понятие напряжения. Пусть даны две точки А и B (рис.1.1), которые находятся в электромагнитном (ЭМ) поле.

Как известно, ЭМ поле характеризуется векторами напряженностей и , где некоторая точка, в которой присутствует это поле. На рисунке сплошными линиями показаны силовые линии электрического поля, а пунктирными – магнитного поля для некоторого момента времени .

Из электродинамики известно, что для упрощения решения уравнений Максвелла достаточно ввести вспомогательные функции векторного и скалярного потенциалов, заданных в каждой точке в любой момент времени и связанных с искомыми напряженностями следующим образом:

, . (1.1)

По смыслу, электрический потенциал точки – работа, которую нужно совершить, чтобы переместить единичный заряд из бесконечности в данную точку.

Под разностью потенциалов или напряжением между точками А и B в момент времени будем понимать скалярную величину

. (1.2)

Напряжение по смыслу есть работа по перемещению единичного заряда из одной точки поля в другую.

Понятие электрического тока. Электрический ток – направленное движение заряженных частиц. Например, в электролитах и газах под действием электрического поля с вектором напряженности движутся навстречу друг другу положительно и отрицательно - заряженные ионы (рис.1.2).

Так как направления движения разно-заряженных ионов противоположны (вектор скорости положительных ионов противоположен вектору скорости отрицательно – заряженных ионов ), то необходимо договориться о том, направление движения каких ионов следует считать направлением тока. За направление тока принято считать направление движения положительно заряженных ионов.

Рассмотрим теперь участок проводника (рис.1.3).

Е сли через поперечное сечение за интервал времени проходит электрический заряд общей величины , то говорят, что величина среднего тока на интервале от до равна . Устремим теперь к нулю. Тогда придем к понятию мгновенного тока в момент времени :

, (1.3)

где функция - имеет смысл заряда, прошедшего к моменту времени через поперечное сечение проводника.

Таким образом, мгновенный ток имеет смысл скорости изменения прошедшего заряда в данный момент времени.

На рис.1.4 показано несколько зависимостей и соответствующие им зависимости .

Из рис.1.4а следует, что если заряд, проходящий через выделенное поперечное сечение проводника, линейно растет с течением времени, то ток постоянен и тем больше по величине, чем больше коэффициент пропорциональности , стоящий перед в выражении для . Таким образом, чтобы через проводник тек постоянный ток, необходимо, чтобы функция была линейной: . Тогда коэффициент пропорциональности будет равен мгновенному току: .

Если зависимость экспоненциальная (рис.1.4б), то ток также будет меняться по экспоненциальному закону; чем больше коэффициент , стоящий перед в показателе экспоненты, тем быстрее изменяется ток.

Если - гармоническая функция (рис.1.4в), то - тоже гармоническая функция.

Рассмотрим электрическую схему, приведенную на рис.1.5.

Здесь омическое сопротивление (или просто сопротивление) есть идеализированный элемент схем, приближенно соответствующий реальному элементу электрических цепей – резистору. В резисторе происходит преимущественное преобразование электрической энергии в неэлектрическую, например, в тепловую. В отличие от реального резистора омическое сопротивление как идеализированный элемент схем учитывает только преобразование электрической энергии в тепловую.

По поводу резистора вспомните закон Джоуля – Ленца из курса школьной физики. Он дает связь между мгновенными током и напряжением, приложенными к резистору, и джоулевой энергией, выделяющейся на нем за интервал времени .

Емкость – идеализированный элемент схем, приближенно соответствующий реальному элементу электрических цепей – конденсатору, который является аккумулятором преимущественно электрической энергии.

Индуктивность - идеализированный элемент схем, приближенно соответствующий катушке индуктивности - реальному элементу электрических цепей, который является аккумулятором преимущественно магнитной энергии.

При описании резистора, индуктивности и емкости мы употребили слово “преимущественно” не зря. Хотя для практических целей нас интересуют именно эти их свойства, однако в реальности каждый из указанных трех реальных элементов цепей обладает частично свойствами двух других. Однако мы можем ими в первом приближении пренебречь.

Идеальный источник напряжения или ЭДС (ИИЭ) на схеме – идеализированный элемент (ИЭ) схем, который является моделью реального источника напряжения, назначение которого – выдавать в цепь постоянное либо переменное напряжение. Для ИИЭ полагается, что напряжение, выдаваемое им во внешнюю часть схемы, не зависит от тока, протекающего через него.

Идеальный источник тока (ИИТ) – идеализированный элемент схем, являющийся моделью реального источника тока, функция которого – выдавать в цепь либо постоянный, либо переменный ток. Для ИИТ считается, что ток, выдаваемый им во внешнюю часть схемы, не зависит от напряжения, приложенного к нему.

При анализе электрических цепей направления тока и напряжения, соответствующих идеализированному элементу, выбираются произвольно, поскольку ток и напряжение как функции времени являются алгебраическими величинами. Важно только, чтобы они были согласованы между собой (т.е. куда направлен ток – туда направлено и напряжение). Однако для удобства принято, что направление тока в ветви с ИИЭ выбирается по направлению ЭДС; а в ветви с ИИТ - по направлению стороннего тока ИИТ. Во всех остальных ветвях направления токов выбираются произвольно. Направления напряжений на каждом ИЭ некоторой ветви выбираются такими же, как и направление тока этой ветви (см. рис.1.5).

Из школьного курса вам известно, что для резистора связь между напряжением, приложенным к нему, и током, текущим через него, описывается законом Ома. Аналогичные связи существуют между током и напряжением других идеализированных элементов схем.

Математически связь между мгновенными током и напряжением на некотором ИЭ описывается полюсными уравнениями.

Полюсные уравнения

для:

линейного омического сопротивления:

, (1.4)

если , то резистор называется нелинейным;

линейной индуктивности:

, (1.5)

если , где - суммарный магнитный поток, пронизывающий витки катушки индуктивности, то индуктивность - нелинейная;

линейной емкости:

(1.6)

если , где - заряд, накопленный на обкладках конденсатора к моменту времени , то емкость является нелинейной;

постоянного ИИЭ:

; (1.7)

постоянного ИИТ:

. (1.8)

У равнение (1.4) есть знакомый вам закон Ома для резистивного сопротивления. Полюсное уравнение линейного индуктивного элемента (1.5) связано с законом электромагнитной индукции: если ток, текущий через индуктивность, меняется во времени, то меняется и магнитное поле, точнее, его поток, пронизывающий

витки индуктивности. Этот переменный во времени магнитный поток порождает электродвижущую силу самоиндукции, которой эквивалентно напряжение, направленное по направлению тока в данный момент времени. На рис.1.6 показаны силовые линии переменного магнитного поля, пронизывающие катушку, направление тока и наводимого напряжения в фиксированный момент времени. Если ток меняется гармонически, то указанные направления также будут меняться с периодом изменения функции .

Из полюсного уравнения линейной емкости (1.6) следует, что ток, протекающий через емкость, не равен нулю, только если напряжение, приложенное к обкладкам конденсатора, переменно во времени.

Действительно, вам известно соотношение между напряжением , приложенным к емкости постоянной величины (рис.1.7), и зарядом , накопленным на ее обкладках:

. (1.9)

Напомним, что заряды, накапливаемые к некоторому моменту времени на обкладках конденсатора, равны по величине и противоположны по знаку. Возьмем производную от обеих частей выражения (1.9) и учтем равенство для мгновенного тока (1.3). Получим:

, что совпадает с полюсным уравнением (1.6).

Итак, электрическая схема – модель реальной электрической цепи, приближенно представляющая эту цепь в виде идеализированных элементов, связанных между собой.

Эти связи между идеализированными элементами отражают структурные, или топологические, свойства цепи.

В электротехнике для описания структурных свойств цепи применяется понятие графа. Так, схеме, изображенной на рис.1.5, соответствует граф, показанный на рис.1.8.

Введем несколько понятий, связанных с понятием графа.

Ветвь – участок схемы, по которому идет один и тот же ток.

Узел – место соединения трех и более ветвей.

Контур – замкнутая линия, проходящая по разным ветвям схемы. Контур характеризуется направлением обхода, которое выбирается произвольно: по или против часовой стрелки.

Дерево схемы – совокупность отрезков прямых, соединяющих все узлы схемы, но не образующих замкнутых контуров. Ветви с источниками тока не входят в дерево.

Граф схемы получается, если дерево достроить недостающими ветвями (называющимися главными). Ветви с источниками тока обозначаются на графе пунктирными линиями.

Например, схема на рис.1.5 имеет 3 узла, 5 ветвей, из которых одна включает идеальный источник тока. В схеме имеется 3 контура. Дерево данной схемы может быть образовано ветвями 2 и 3 (определить другие деревья этой схемы). Ветви 1 и 3 являются для выбранного дерева главными.

Теперь рассмотрим схему на рис.1.9а. Здесь точки , и , являются по определению узлами. Однако электрические потенциалы точек и в любой момент времени одинаковы. То же можно сказать и о точках и . Поэтому пары простых узлов ( , ) и ( , ) можно объединить в обобщенные узлы и соответственно. В результате получим схему, приведенную на рис.1.9б.

Алгебраическое выражение структурных свойств электрических цепей дается законами Кирхгофа.

Первый закон Кирхгофа.

Алгебраическая сумма мгновенных значений токов, входящих или исходящих из каждого узла, в любой момент времени равна нулю. Если некоторый ток исходит из узла, то он берется с плюсом, иначе – с минусом, т.е.:

, (1.10)

где - номер некоторого узла, - число всех узлов схемы; - число ветвей, связанных с данным узлом; , , …, - токи, текущие в -й, 2-й,…, -й ветвях соответственно.

Число независимых уравнений , которые можно составить для некоторой схемы по первому закону Кирхгофа, на единицу меньше числа узлов:

. (1.11)

Например, для схемы, показанной на рис.1.5, используя узлы 1 и 2 (см. рис.1.8), получаем такие уравнения по первому закону Кирхгофа:

(1.12)

Для каждой схемы имеется всего способов составления уравнений по первому закону Кирхгофа (обосновать). Каждому способу соответствует некоторая совокупность из ( ) узлов схемы. Выбор того или иного способа диктуется соображениями удобства.

Для формулировки следующего закона введем понятие независимого контура.

Представим дерево графа. Если добавить к дереву одну из главных ветвей, то последняя вместе с некоторыми ветвями дерева образует контур. Контур может быть образован также с помощью нескольких главных ветвей и ветвей дерева. Каждый контур, полученный в результате этих двух процедур, может быть независимым контуром.

Пусть указанными выше способами выбрана совокупность из

, (1.13)

( - число всех ветвей, - число ветвей, содержащих источники тока)

контуров. В этом случае каждый из них является независимым, и вместе они образуют совокупность независимых контуров (СНК). Очевидно, СНК может быть выбрана неоднозначно.

Второй закон Кирхгофа.

Для каждого независимого контура из некоторой СНК алгебраическая сумма мгновенных значений напряжений на всех ИЭ, входящих в данный контур, в любой момент времени равна алгебраической сумме всех ЭДС, действующих в этом контуре. Если некоторое напряжение или ЭДС совпадает с выбранным направлением обхода контура, то они берутся с плюсом, иначе – с минусом, т.е.:

, (1.14)

где - номер независимого контура, входящего в данную СНК; - число элементов и число источников ЭДС, входящих в - й независимый контур.

Число независимых уравнений, которые можно составить по второму закону Кирхгофа для некоторой схемы, равно . Ясно, что число различных способов составления уравнений по второму закону равно числу возможных СНК.

Для схемы, приведенной на рис.1.5, таких СНК всего три: , , . Например, для СНК имеем такую систему (сопоставляем рис.1.5 и 1.8):

(1.15)

В последнем уравнении в правой части стоит ноль, так как в контуре нет ни одного источника ЭДС.

Конечной целью математического анализа электрической схемы является нахождение мгновенных значений токов во всех ветвях и напряжений на всех элементах.

Для нахождения этих функций необходимо дополнить топологические уравнения (1.10), (1.14) полюсными – (1.4)-(1.8). В результате получим систему интегро-дифференциальных уравнений с постоянными (для линейных ИЭ) либо переменными (в случае наличия хотя бы одного нелинейного ИЭ) коэффициентами.

Поскольку число неизвестных функций тока равно числу ветвей, не содержащих ИИТ, т.е. , а число искомых функций напряжения равно числу всех пассивных элементов (не источников энергии), то число уравнений для указанных искомых функций, равное , как раз равно общему числу неизвестных функций.

Например, дополняя топологические уравнения схемы на рис.1.5 полюсными уравнениями всех ее элементов, считая последние линейными, получим систему:

(1.16)

где учтено, что .

Рассмотрим теперь понятие мгновенной мощности.

Под мгновенной электрической мощностью в момент времени некоторого элемента цепи будем понимать произведение его мгновенных тока и напряжения :

. (1.17)

Тогда, взяв интеграл от (1.17) в пределах , найдем энергию, которая потребляется или отдается некоторым элементом цепи за данный интервал времени:

. (1.18)

Примечание. Напомним, что интеграл геометрически есть площадь под кривой интегрируемой функции. Например, интеграл (1.18) равен площади фигуры на рис. 1.10а, если график функции лежит только выше оси . В случае, когда кривая лежит одной своей частью выше оси , а другой – ниже, то этот интеграл есть разность площадей и (рис.1.10б).

Рассмотрим величины (1.17) и (1.18) для всех элементов цепи.

Мгновенная мощность и энергия для сопротивления равны

, (1.19)

. (1.20)

Из (1.19) и (1.20) следует, что сопротивление в любой момент времени только потребляет энергию от источника (поскольку для любого ), поэтому для любого интервала .

Для емкости, воспользовавшись (1.6), получим:

. (1.21)

Из выражения (1.21) следует, что емкость может и принимать и отдавать электрическую энергию в цепь (может отдать не больше, чем приняла от источников энергии, так как является пассивным элементом). Поэтому обычно интересуются энергией (электрической), накопленной емкостью к моменту времени :

. (1.22)

Для индуктивности имеем:

. (1.23)

Следовательно, индуктивность также может и потреблять энергию из цепи, и отдавать ее в цепь (являясь пассивным элементом, отдает не более, чем принимает от источников энергии). Энергия (магнитная), запасенная в индуктивности к моменту времени , равна:

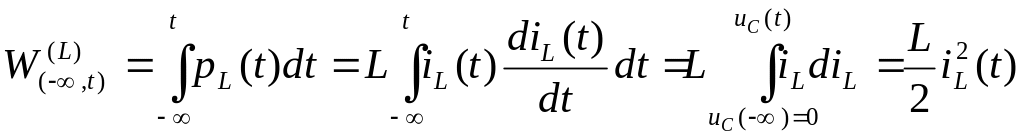. (1.24)

Для обоснования факта, что индуктивность и емкость могут иметь как положительную, так и отрицательную мгновенную мощность, вспомните явления, происходящие в электрическом колебательном контуре. Если источник энергии (источник ЭДС на рис.1.11) меняется гармонически, то в течение части периода изменения сигнала емкость потребляет электрическую энергию от источника, а индуктивность – отдает магнитную энергию в цепь, а в течение другой части – наоборот, емкость отдает накопленную ранее энергию в цепь, а индуктивность – потребляет магнитную энергию из цепи. Если в колебательном контуре есть омическое сопротивление, то часть энергии источника будет тратиться на тепловые потери в контуре, вследствие чего амплитуда колебаний будет затухать.

В заключение данного раздела приведем два примера из схемотехники на применение законов Кирхгофа.