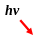Метод решения уравнения Шредингера, в котором вид периодического потенциала решетки автоматически учитывается через эффективную массу, называется методом эффективной массы

В общем случае эффективная масса является анизотропной величиной и для разных направлений волнового вектора различна. Она представляет собой тензор второго ранга:

или 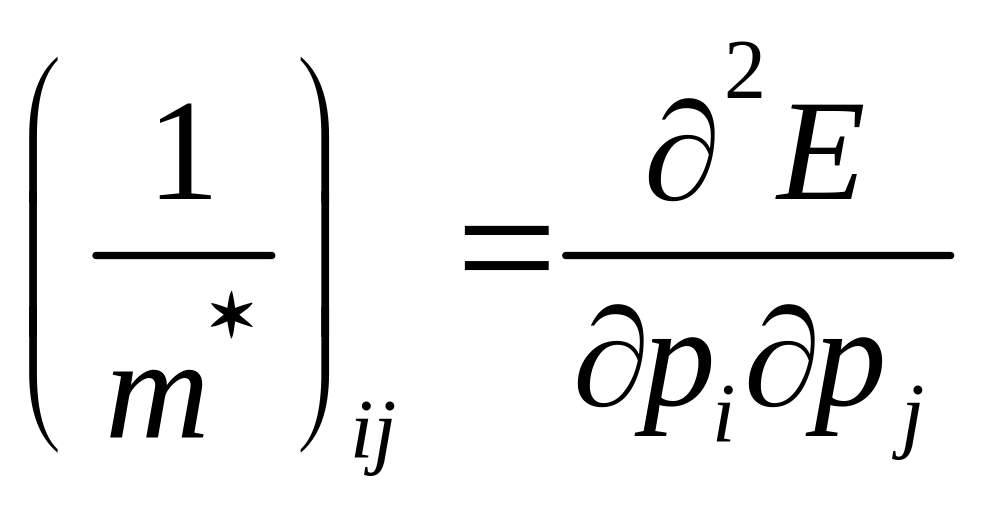(1.83)

Таким образом, если зависимость [закон дисперсии] анизотропна, то эффективная масса представляет собой тензор обратных эффективных масс.

Рассмотрим некоторые свойства эффективной массы.

Из формул (1.74), (1.81), (1.85) следует, что эффективная масса определяется видом дисперсионной зависимости E(k). В приближении сильной связи выражение E(k) имеет вид (1.70), как это следует из модели Кронига-Пенни. Периодичность волновой функции (1.51), (1.52) и энергии электрона в кристалле (1.54) позволяет ограничиться рассмотрением зависимости E(k) в первой зоне Бриллюэна. Возьмем первую (нижнюю) ветку дисперсионной кривой E(k) в первой зоне Брилюэна для кристалла кубической сингонии (рис. 1.48а) и проведем дифференцирование. Поскольку E(k) имеет функциональную зависимость, близкую к E(k) ~ cos (ka) (см. формулу (1.70)), первая производная вблизи точек экстремума будет близкой к зависимости dE/dk ~ sin (ka). Во всей первой зоне Бриллюэна, зависимость dE/dk есть зависимость скорости электрона от волнового вектора k: (dE/dk=V_g).

Вторая производная и ее обратная зависимость (пропорциональная эффективной массе) приведены на рис. 1.48. Сравнение зависимости E(k) на рис. 1.48(а) и зависимости m*(k) на рис. 1.48(г) позволяет сделать следующие комментарии. Электрон, находящийся внутри идеальной периодической решетки может иметь как положительную, так и отрицательную эффективную массу. Если кривая на диаграмме E-k имеет выпуклость вниз (относительно оси энергий, если принять направление увеличения энергии - вверх), то масса m*>0. Если же кривая имеет выпуклость вверх (около ), тогда m*<0.

Отрицательная эффективная масса означает, что ускорение электрона направлено против действия внешней силы. Это видно из рис. 1.48б. При k, близких к границе зоны Бриллюэна, несмотря на увеличение k, скорость электрона уменьшается. Данный результат является следствием брэгговского отражения. В точке k= — состояние электрона описывается уже не бегущей, а стоячей волной и =0. В случае, когда m*<0 (на рис. 1.48(г) это области –π/a<k<π/2a и π/2a<k<π/a), частица будет ускоряться в направлении, противоположном направлению движения нормального (отрицательно заряженного) электрона; т.е. будет вести себя как некоторая гипотетическая частица, с положительным зарядом и положительной массой. Поскольку свойства электронов с отрицательной эффективной массой очень сильно отличаются от свойств "нормальных" электронов, их удобнее описывать, пользуясь представлением о некоторых квазичастицах, имеющих заряд +е, но и положительную эффективную массу. Такая, квазичастица¹ получила название дырка. Обозначение дырки – h (от англ. «hole»).

	A
Рис. 1.48. Зависимость энергии (а), скорости (которая ~ dE/dk) (б), величины d2E/dk2 (в) и эффективной массы (г) от волнового вектора для кубической решетки.	Рис. 1.49. Схема перемещения связанных носителей (электронов) и свободных носителей (дырок) внутри валентной зоны.

Понятие дырки поясним следующим примером (рис. 1.49):

Предположим, в исходном состоянии валентная зона полностью заполнена электронами (нет свободных энергетических уровней), а зона проводимости – свободна. Включив внешний приток энергии (нагрев, облучение светом, радиацией и др.), можно инициировать переход электронов из валентной зоны в зону проводимости. Предположим далее, что энергия фотона передаётся электрону в валентной зоне и он переходит в зону проводимости (процесс А на рис. 1.49). С точки зрения химической связи это означает повреждение (разрыв) ковалентной связи и уход электрона в свободное перемещение по кристаллу. С точки зрения зонной теории, электрон уходит в зону проводимости, а на потолке валентной зоны образуется незанятое место (квантовое состояние).

Если внешнее электрическое поле E равно нулю и вследствие того, что электроны стремятся занять самые нижние энергетические состояния, дырка занимает самое верхнее состояние (позицию 1 на рис. 1.49). Под действием электрического поля E на это незанятое состояние перейдет электрон с более низкого энергетического уровня: на рис. 1.49 это обозначено переходом электрона из позиции 2 в позицию 1. Дырка при этом опустится из позиции 1 в позицию 2. Затем этот процесс может повториться переходом (3  2) и т.д. по эстафете. При таком перемещении электронов, освобождающееся незанятое место на энергетическом уровне перемещается вниз, вглубь валентной зоны. Этот освобождающийся уровень и отождествляется с некоей фиктивной частицей, которая имеет равный по значению, но противоположный по знаку заряд, по сравнению с электроном. Таким образом, свободное от электрона квантовое состояние вблизи потолка валентной зоны и называют дыркой.

Важно отметить, что при переходах 1  2  3 … дырка приобретет кинетическую энергию, и полная энергия дырки возрастет (!!!), т.е. шкала энергий в валентной зоне возрастает в направлении – противоположном зоне проводимости.

Классический аналог увеличения энергии по зонам: взвешенная капля воды в воздухе (туман) – электрон в зоне проводимости, пузырек воздуха в воде – дырка в валентной зоне.

Таким образом, ток в кристаллах может переноситься не только электронами в зоне проводимости, но и дырками в валентной зоне. Дырочная проводимость наиболее характерна для полупроводников, однако есть и некоторые металлы, которые обладают дырочной проводимостью.

Возвращаясь к рис. 1.48в, отметим, что описывать движение электронов в кристалле, пользуясь понятием эффективной массы, можно только тогда, когда они находятся либо у дна, либо у потолка энергетической зоны. В центре зоны (около значений k = ± π/a) m*∞, т.е. понятие эффективной массы теряет смысл. На практике почти всегда приходится иметь дело с электронами, располагающимися или у дна, или у потолка зоны. Поэтому использование эффективной массы в этих случаях вполне оправдано.

Ширина разрешенных зон растет, а запрещенных – уменьшается, с увеличением энергии (порядкового номера разрешенной зоны). Т.е. в общем случае зона проводимости, имеет большую ширину, чем валентная зона. Поскольку эффективная масса обратно пропорциональна ширине энергетической зоны, поэтому, как правило, . Следовательно, дырка и электрон проводимости отличаются не только знаком своего заряда, но имеют и разные по величине m*.

Иной результат получается, если в почти заполненной зоне имеются свободные места, то есть не все валентные связи обеспе­чены электронами. Тогда соседние электроны могут переходить на эти места, а само свободное место как бы перемеща­ется в пространстве. В энергетическом плане это соответству­ет переходу электронов с низких энергетических уровней на более высокие, а дырок с высоких уровней на более низкие.

Резюмируя полученную информацию:

1. Обозначения носителей зарядов в полупроводнике.

Электроны	n, e (negative, electrons)
Дырки	p, h (positive, holes)
Ток частично заполненной зоны может быть представлен как ток положительно заряженных частиц дырок. Заряд дырки положителен и по величине равен заряду электрона. Концентрация дырок обычно обозначается буквой р.

2. Три представления (определения) дырок:

(a) полноправная положительно заряженная частица, перемещающая в кристалле.

(b) отсутствие электрона в потолке валентной зоны.

(c) физическое отсутствие электрона в том месте, где он должен быть в равновесном состоянии – т.е. в составе ковалентной связи.

3. Направление энергии в зонах: зона проводимости – энергия увеличивается вверх; валентная зона – энергия увеличивается вниз.

4. Величина m* зависит от кривизны зоны (m* ~ (d²E/dk²)^-1)

5. Ширина зон увеличивается с E, а m^* обратно пропорциональна ширине энергетической зоны,  (a) зона проводимости энергетически шире, чем валентная; (b) (как правило).

1.3.5. Циклотронный (диамагнитный) резонанс

Величину эффективной массы носителей заряда можно определить, используя циклотронный резонанс. В этом случае полупроводник помещают в постоянное магнитное поле с индукцией В= const. На электрон, движущийся со скоростью v, будет действовать сила Лоренца

F = - q[vB], (1.84)

Под действием этой силы электрон будет двигаться по окружности, плоскость которой перпендикулярна вектору постоянного магнитного поля В.

Из равенства центробежной силы и силы Лоренца

, (1.85)

а скорость v = ω_cr (где ω_c – циклическая частота) из (1.85) получим:

(1.86)

С учетом квантовой природы электронов эта формула приобретает вид:

(1.87)

где l — орбитальное квантовое число.

Энергия этого орбитального движения соответственно будет

(1.88)

Переменное высокочастотное поле, вектор E которого направлен перпендикулярно B, способно перебросить электрон с одной орбиты на другую так, чтобы = ±1. Для этого потребуется энергия

(1.89)

Это может иметь место только при определенной частоте высокочастотного поля, равной .

(1.90)

и именуемой циклотронной частотой. Из последнего соотношения следует, что циклотронная частота не зависит от скорости и радиуса окружности.

Таким образом, если в полупроводнике создать слабое высокочастотное (~ Ггц) электрическое поле, колеблющееся в плоскости, перпендикулярной B, то при приближении частоты поля к электрон будет сильно поглощать энергию электромагнитного поля. Это явление резонансного поглощения принято называть циклотронным резонансом.

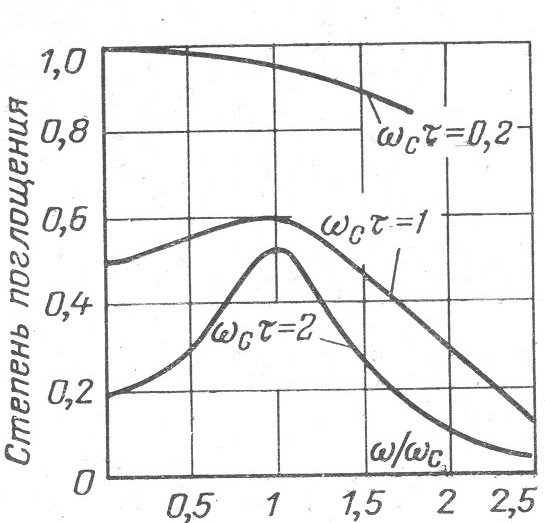
Рис.1.50.Степень поглощения при циклотронном резонансе в зависимости от напряженности постоянного магнитного поля ( в единицах ).	Рис.1.51. Поглощение при циклотронном резонансе в германии.

В циклотроне реализуется аналогичная картина: электроны вращаются в постоянном поле по круговой траектории, получают после каждого оборота энергию от высокочастотного поля и изменяют свою траекторию. Этот процесс повторяется до тех пор, пока электроны не накопят достаточную энергию, после чего выводятся из циклотрона. Поэтому и резонанс получил название циклотронного. Так как по правилу Ленца изменение магнитного потока через электрический контур индуцирует в контуре ток, магнитный эффект которого будет противодействовать указанному изменению, то в цепи без сопротивления, которой является электронная орбита атома, индуцированный ток сохраняется пока существует поле. Магнитный момент связанный с этим током есть диамагнитный момент. Поэтому такой резонанс сразу после его открытия Я. Г. Дорфманом был назван диамагнит­ным, но впоследствии укоренилось название циклотронного.

Так как поле является относительно слабым, а энергия связи электрона с ядром сравнительно велика (1-10 эВ), то циклотронный резонанс будет происходить только на свободных электронах или дырках, т. е. на носителях заряда, находящихся в разрешенных зонах. Кроме того, циклотронный резонанс можно экспериментально наблюдать, если полученная от высокочастотного поля энергия не успеет рассеяться за период колебаний поля Т=1/v. Следовательно,  — время между двумя последовательными столкновениями (время свободного пробега, время жизни и т.д.) при рассея­нии энергии должно быть много больше Т (или ), чтобы за время Т электрон успел совершить хотя бы один оборот. Чем больше электрон делает оборотов, тем резче (острее) проявляется резонанс.

Время свободного пробега  носителей заряда тем больше, чем меньше в кристалле структурных несовершенств. Поэтому эксперименты по циклотронному резонансу необходимо проводить при очень низких температурах (обычно при 4,2 К) и на особо чистых кристаллах, у которых еще не сказывается примесный механизм рассеяния носителей заряда. Обычно на опыте задается частота радиоизлучения, а резонанс достигается изменением индукции магнитного поля.

Измеряя на опыте значение циклотронной частоты и напряжен­ности постоянного магнитного поля, из (1.90) можно получить значение эффективной массы носителей заряда. Исследуя с помощью циклотронного резонанса m* в кристаллах, различно ориентированных по отношению к магнитному полю сво­ими кристаллографическими плоскостями, удается изучать анизо­тропию эффективной массы, т. е. анизотропию зонной структуры полупроводника.