
- •1.3.4. Эффективная масса носителей заряда
- •(Б) Определение эффективной массы из квазиклассического подхода.
- •Метод решения уравнения Шредингера, в котором вид периодического потенциала решетки автоматически учитывается через эффективную массу, называется методом эффективной массы
- •1.3.6. Зонная структура некоторых полупроводников
1.3.4. Эффективная масса носителей заряда
На
свободный электрон, помещенный в
однородное электрическое поле E,
действует сила F=-qE,
под действием которой электрон приобретает
ускорение
![]() .
Здесь
т
—
масса электрона. Поскольку
.
Здесь
т
—
масса электрона. Поскольку
![]() является единственной силой, определяющей
характер движения частицы,
вектор ускорения электрона направлен
так же, как и вектор внешней силы, т.е.
против поля E.
является единственной силой, определяющей
характер движения частицы,
вектор ускорения электрона направлен
так же, как и вектор внешней силы, т.е.
против поля E.
В
кристалле, внешнее поле E
действует на электрон так же, как на
свободный электрон: с силой F=-qE,
направленной против поля. Однако, кроме
силы -qE,
на электрон действуют значительные
внутренние силы, создаваемые периодическим
полем решетки. Это означает, что ускорение
электрона в решетке в общем случае может
быть не направлено параллельно внешней
силе
![]() .
Следовательно, движение электрона в
кристалле будет более сложным, чем
движение свободного электрона. Именно
поэтому энергия электрона, движущегося
в периодическом поле кристалла, не имеет
квадратичной зависимости от волнового
вектора E
≠ p2/2m.
Это
также следует из теоретических моделей
(например, модели Кронига и Пенни). Однако
для практических целей иногда удобно
сохранить зависимость энергии электрона
от квазиимпульса в классическом виде,
а все различия, вызванные влиянием
периодического поля, включить в массу
электрона. Тогда формулу Е
.
Следовательно, движение электрона в
кристалле будет более сложным, чем
движение свободного электрона. Именно
поэтому энергия электрона, движущегося
в периодическом поле кристалла, не имеет
квадратичной зависимости от волнового
вектора E
≠ p2/2m.
Это
также следует из теоретических моделей
(например, модели Кронига и Пенни). Однако
для практических целей иногда удобно
сохранить зависимость энергии электрона
от квазиимпульса в классическом виде,
а все различия, вызванные влиянием
периодического поля, включить в массу
электрона. Тогда формулу Е![]() р2/2m
можно переписать в виде Е=р2/2m*,
где вместо т
появляется некоторая величина т*,
которая является функция
энергии,
и которая называемая эффективной
массой.
Для
определения понятия эффективной массы
можно воспользоваться несколькими
подходами.
р2/2m
можно переписать в виде Е=р2/2m*,
где вместо т
появляется некоторая величина т*,
которая является функция
энергии,
и которая называемая эффективной
массой.
Для
определения понятия эффективной массы
можно воспользоваться несколькими
подходами.
(а) Определение эффективной массы из разложения в ряд Тейлора (формальный, математический метод). В одномерном случае величину т* можно рассчитать из разложения энергии в ряд Тейлора около экстремальных точек (т. к. E(k)- периодическая функция k и E(k)~cos(k) (периодический член))
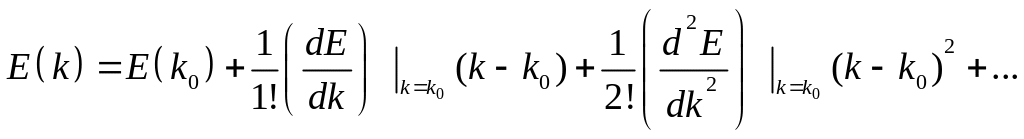 (1.71)
(1.71)
Так как в точках k=ko энергия имеет максимум или минимум (см. рис. 1.46, 1.47), то первая производная равна нулю. Ограничиваясь вторым приближением, из (1.71) находим:
![]() (1.72)
(1.72)
Или: ![]() (1.73)
(1.73)
Если
E(k)-E(k0)=E(k1),
а k-k0=k1,
тогда
![]() ,
,
Следовательно, роль эффективной массы играет величина
![]() (1.74)
(1.74)
В
низших точках разрешенных зон Е(k)
имеет
минимумы, а вторая производная от Е
по k
больше нуля. Поэтому на дне зоны
эффективная масса положительна, а в
вершинах зон отрицательна, поскольку
d2E/
dk2<0.
В некоторой точке в центре зоны m*
![]() .
Очевидно, разложение энергии в степенной
ряд (1.71)
и формула (1.74)
справедливы только вблизи точек
экстремума.
.
Очевидно, разложение энергии в степенной
ряд (1.71)
и формула (1.74)
справедливы только вблизи точек
экстремума.
(Б) Определение эффективной массы из квазиклассического подхода.
Понятие эффективной массы имеет более широкие границы применимости и может быть введено исходя из принципа соответствия. Известно, что средние квантовомеханические величины удовлетворяют тем же соотношениям, что и соответствующие им классические величины. Так, волновые пакеты, составленные из решений уравнения Шредингера, движутся по траекториям классических частиц. Поэтому уравнению Ньютона должен соответствовать квантовомеханический аналог, то есть квантовомеханическое уравнение движения электрона в кристалле.
Таким
образом, можно использовать квазиклассический
подход (наполовину классический,
наполовину квантовомеханический). В
этом подходе квантовомеханическим,
является определение электрона как
волны. В этом случае движение электрона
в кристалле можно описать с помощью
волнового пакета, составленного из
блоховских функций. Тогда средняя
скорость движения электрона равна
групповой
скорости
распространения всего
волнового
пакета
-
![]() .
Учитывая,
что
.
Учитывая,
что
![]() ,
для групповой скорости получаем:
,
для групповой скорости получаем:
![]() (1.75)
(1.75)
Аналогичным образом можно ввести усредненное ускорение волнового пакета (электрона) в кристалле:
![]() (1.76)
(1.76)
С учетом того, что время и квазиимпульс независимы, в (1.76) можно поменять местами порядок их дифференцирования:
![]() (1.77)
(1.77)
Классическим, в настоящем подходе, является определение работы внешней силы над рассматриваемым электроном, которая приводит к увеличению энергии (скорости) электрона:
![]() ,
откуда
,
откуда
![]() или
или
![]() (1.78)
(1.78)
Подставляя (1.78) в (1.77) и учитывая, что внешняя сила F не зависит от k, получим:
![]() (1.79)
(1.79)
Перепишем
в виде:
![]() (1.80)
(1.80)
Т.е.
по аналогии с законом Ньютона, величину
![]()
![]() можно назвать массой электрона:
можно назвать массой электрона:
 (1.81)
(1.81)
Величина т* получила название эффективной массы электрона. Эффективная масса отражает влияние периодического потенциала решетки на движение электрона в кристалле под действием внешней силы. В периодическом поле кристаллической решетки электрон движется под действием внешней силы F в среднем так, как двигался бы свободный электрон под действием этой силы, если бы он обладал массой т* Таким образом, если электрону в кристалле вместо массы т приписать эффективную массу т*, то его можно считать свободным и движение этого электрона описывать так, как описывается движение свободного электрона, помещенного во внешнее поле. Разница между т* и m обусловлена взаимодействием электрона с периодическим полем решетки, и, приписывая электрону эффективную массу, мы учитываем это взаимодействие.
Эффективная масса, в отличие от обычной массы, не определяет ни инерционных, ни гравитационных свойств частицы. Она является лишь коэффициентом в уравнении движения и отражает меру взаимодействия электрона с кристаллической решеткой. |
Пользуясь
понятием эффективной массы, задачу о
движении электрона в периодическом
поле решетки V(![]() )
можно свести к задаче о движении
свободного электрона с массой т*.
Это значит, что вместо уравнения
Шредингера с периодическим потенциалом
)
можно свести к задаче о движении
свободного электрона с массой т*.
Это значит, что вместо уравнения
Шредингера с периодическим потенциалом
![]() ,
нужно
решать уравнение
,
нужно
решать уравнение
![]() ,
(1.82)
,
(1.82)
