2. Зависимость силы тяги от скорости

Существует два режима движения локомотива, при которых сила тяги зависит от скорости различным образом. При движении со сравнительно небольшой скоростью, вплоть до так называемой критической скорости, запас мощности двигателей достаточен для создания предельной силы тяги. Сила тяги в этом режиме ограничена только потерей сцепления колеса с рельсом. Результаты экспериментальных измерений свидетельствуют о том, что предельная сила тяги сильно зависит от состояния материала, качества обработки и износа рельсов и колес, от погоды и еще большого числа факторов. Однако тенденция уменьшения предельной силы тяги с ростом скорости существует (рис. 3.3). Причиной этого может быть уменьшение времени процесса пластической деформации микробугорков в пятнах контакта при увеличении скорости движения. Поэтому число межмолекулярных связей между металлом колеса и рельса с ростом скорости тоже уменьшается, и это приводит к уменьшению силы тяги.

При движении со скоростью выше критической мощность двигателей достигает номинального значения и уже недостаточна для поддержания предельной силы тяги. По формуле мощности сила тяги уменьшается обратно пропорционально скорости:

. (3.3)

(Это похоже на уменьшение силы отталкивания бегуна от беговой дорожки по мере увеличения его скорости.)

З начение критической скорости V_кр можно определить, приравняв предельные значения силы тяги по сцеплению и по мощности (3.3) друг к другу

. (3.4)

3. Сила трения качения

П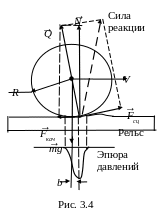 ри качении колеса по рельсу происходит деформация как колеса, так и рельса. Из-за остаточных деформаций уровень рельса за колесом оказывается ниже, чем перед колесом, поэтому колесо при движении должно все время закатываться на бугорок. Распределение давления на колесо со стороны рельса оказывается несимметричным: спереди давление больше, а сзади меньше (рис. 3.4). Точка приложения силы реакции рельса на колесо смещается вперед на небольшое расстояние b.

Разложим силу реакции на две компоненты. Нормальная составляющая реакции Q перпендикулярна площадке контакта и проходит через ось колеса, а касательная составляющая F_сц направлена почти вдоль рельса. Это сила сцепления. Она препятствует проскальзыванию колеса по рельсу. Разложим, в свою очередь, нормальную составляющую силы реакции Q на две компоненты: перпендикулярно рельсу N, и силу, направленную вдоль рельса, которая является силой трения качения F_кач.

Так как сила Q проходит через ось колеса, то сумма моментов сил ее составляющих относительно оси должна быть равна нулю: . Откуда получаем, что сила трения качения пропорциональна силе давления рельса на колесо:

. (3.5)

Здесь – коэффициент трения качения. Он уменьшается с ростом твердости материала рельса и колеса и с увеличением размеров колеса. Если бы за колесом при идеально упругих свойствах металла форма рельса восстанавливалась, то эпюра давления была бы симметричной, и трение качения отсутствовало бы.

Итак, в зоне контакта действуют две силы трения: диссипативная сила трения качения, направленная против скорости и консервативная сила сцепления, являющаяся силой трения покоя. При буксовании или юзе колеса сила сцепления превращается в диссипативную силу трения скольжения. На сопротивление при качении колеса влияет состояние железнодорожного полотна, удары о стыки рельсов, трение в подшипниках колесной пары, удары гребня бандажа о рельсы при извилистом движении колесной пары. Увеличивается сопротивления при движении на повороте, так как гребень переднего колеса упирается о наружный рельс. Вместе с силой трения качения все эти дополнительные воздействия создают общую силу сопротивления движению поезда. Будем считать, что суммарная сила сопротивления качению колес поезда подчиняется закону Кулона, то есть, пропорциональна силе нормального давления рельсов на колеса поезда. Так как сила нормального давления практически равна силе тяжести поезда, то закон для силы сопротивления качению примет вид

F_сопр = μ_сопр M g. (3.6)

По экспериментальным измерениям, результирующий коэффициент сопротивления μ_сопр при качении стального колеса по рельсу, находится в пределах 0,003 – 0,008. Это много меньше, чем коэффициент трения скольжения. Поэтому катить легче, чем тащить. Столь малое значение коэффициента сопротивления обусловило эффективность и широкое распространение рельсового транспорта.