
- •Физические основы механики
- •1. Кинематика поступательного движения
- •1. Основные понятия кинематики
- •2. Скорость
- •3. Ускорение
- •4. Уравнения равнопеременного движения
- •5. Стандартный график движения поезда
- •2. Силы в механике
- •1. Сила тяжести и вес тела
- •2. Силы трения покоя и скольжения
- •3. Аэродинамические силы
- •4. Сила упругости
- •3. Силы в транспорте
- •1. Сила тяги локомотива
- •2. Зависимость силы тяги от скорости
- •3. Сила трения качения
- •4. Сила торможения
- •4. Динамика поступательного движения
- •1. Законы Ньютона
- •2. Движение поезда в режиме постоянной силы тяги
- •3. Движение поезда в режиме постоянной мощности
- •4. Движение поезда при торможении и выбеге
- •5. Неинерциальные системы отсчета
- •Силы инерции
- •2. Движение вагона на повороте
- •3. Опрокидывание вагона на повороте.
- •4. Силы в автосцепках вагонов
- •6. Статика
- •1. Условие равновесия тел
- •2. Сила давления вагона на рельсы
- •3. Стоянка поезда на спуске
- •4. Балластировка локомотива
- •7. Законы сохранения в механике
- •1. Закон сохранения импульса
- •2. Работа
- •3. Кинетическая энергия
- •4. Потенциальная энергия
- •5. Закон сохранения энергии
- •8. Соударение тел
- •1. Явление удара
- •2. Соударение тел
- •3. Сцепление вагонов
- •Параметры кинематики вращательного движения
- •2. Момент силы
- •3. Основной закон динамики вращательного движения
- •4. Расчет момента инерции некоторых тел
- •10. Динамика плоского движения тел
- •1. Движение центра масс
- •1. Плоское движение твердых тел
- •3. Теорема Штейнера
- •4. Ускорение при скатывании вагона
- •11. Кинетическая энергия вращателього
- •1. Кинетическая энергия вращательного движения
- •2. Кинетическая энергия при плоском движении тела
- •3. Скатывание вагона с сортировочной горки
- •4. Аккумулирование энергии маховиком
- •12. Закон сохранения момента импульса
- •1. Момент импульса
- •2. Закон сохранения момента импульс для одного тела
- •3. Закон сохранения момента импульса для системы тел
- •4. Гироскоп
- •13. Релятивистская механика
- •1. Постулаты сто
- •2. Преобразования Лоренца
- •3. Следствия преобразований Лоренца
- •3. Основы релятивистской механики
- •4. Радиолокационный скоростемер.
- •14. Механические колебания
- •1. Уравнение гармонических колебаний.
- •2. Пружинный маятник
- •3. Физический маятник
- •4. Галопирующие колебания вагона
- •15. Затухающие колебания
- •1. Уравнение затухающих колебаний
- •2. Параметры затухания колебаний
- •3. Амортизаторы вагона
- •4. Рессорное подвешивание вагона
- •16. Вынужденные колебания
- •1. Уравнение вынужденных колебаний
- •2. Вибрация электродвигателя
- •17. Волны в упругих средах
- •1. Уравнение волны.
- •2. Интерференция волн
- •3. Скорость распространения упругих волн
- •4. Колебания контактного провода
- •1. Кинематика поступательного движения…………………… …………...………7
14. Механические колебания
Механические колебания – это движение, при котором параметры движения тела (координата, скорость, ускорение и т.д.) периодически повторяются. Различают четыре вида колебаний: собственные, вынужденные, автоколебания и параметрические колебания.
Собственные колебания – это колебания тел, называемых маятниками, обусловленные внутренними силами упругости пружин или сил другой природы, которые направлены к положению равновесия. Если маятник вывести из положения равновесия и отпустить, то под действием возвращающей силы маятник движется к положению равновесия, но по инерции проходит его и отклоняется в противоположном направлении. Затем процесс повторяется в обратном направлении. Если бы не было сил трения, то собственные колебания длились сколь угодно долго. Такие собственные колебания называются свободными.
Вагон, опирающийся на пружины подвески, может совершать собственные колебания. Для этого достаточно вывести его из положения равновесия ударом грузом, вибрацией электродвигателей, ударом колес о стыки рельсов, ударами рельса о гребни колес из-за волнистого характера рельсового пути, виляния колесных пар и т.д.
О тносительно
трех координатных осей вагон может
совершать шесть различных видов колебаний
(рис. 14.1). Существует три вида
возвратно-поступательных
колебаний вагона вдоль трех осей
координат: вертикальные колебания вдоль
оси Оz;
поперечные колебания, или поперечный
относ вдоль оси Oy,;
продольные колебания, или подергивание
вдоль оси Ох;
и три вида вращательных
колебаний
вокруг трех осей координат: галопирование
вокруг оси Oy;
виляние вокруг оси Oz;
бортовая
качка вокруг оси Ох.
В чистом виде ни один из видов колебаний
обычно не реализуется,
вагон всегда участвует во всей совокупности
возможных видов колебаний.
тносительно
трех координатных осей вагон может
совершать шесть различных видов колебаний
(рис. 14.1). Существует три вида
возвратно-поступательных
колебаний вагона вдоль трех осей
координат: вертикальные колебания вдоль
оси Оz;
поперечные колебания, или поперечный
относ вдоль оси Oy,;
продольные колебания, или подергивание
вдоль оси Ох;
и три вида вращательных
колебаний
вокруг трех осей координат: галопирование
вокруг оси Oy;
виляние вокруг оси Oz;
бортовая
качка вокруг оси Ох.
В чистом виде ни один из видов колебаний
обычно не реализуется,
вагон всегда участвует во всей совокупности
возможных видов колебаний.
1. Уравнение гармонических колебаний.
Наиболее распространены гармонические колебания, то есть колебания, подчиняющиеся закону синуса или косинуса. Это происходит, как будет показано далее, если возвращающая сила пропорциональна смещению. Пусть координата тела изменяется в зависимости от времени по закону
![]() .
(14.1)
.
(14.1)
Здесь А – амплитуда колебаний, то есть наибольшее смещение тела от положения равновесия, ω – циклическая частота, равная числу колебаний за 2π секунд. Аргумент косинуса называется фазой, φ – начальной фазой колебаний.
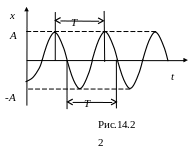
Процесс колебаний
характеризуются периодом колебаний
![]() (рис. 14.2). Это
время одного полного колебания, за
которое фаза колебаний возрастает на
2π радиан.
Кроме того, используется понятие частоты
(рис. 14.2). Это
время одного полного колебания, за
которое фаза колебаний возрастает на
2π радиан.
Кроме того, используется понятие частоты
![]() ,
которая равна числу колебаний в единицу
времени.
,
которая равна числу колебаний в единицу
времени.
Скорость и ускорение при гармонических колебаниях определим как производные от уравнения координаты
![]() , (14.2)
, (14.2)
![]() . (14.3)
. (14.3)
Из вида уравнений
видно, что скорость и ускорение также
изменяются со временем по гармоническим
законам. Ускорение всегда направлено
в сторону, противоположную смещению,
то есть, всегда направлено к положению
равновесия. Ускорение максимально в
крайней точке траектории, при х=А,
и равно
![]() .
Максимальная скорость достигается
телом при x
= 0, в момент
прохождения положения равновесия и
равна
.
Максимальная скорость достигается
телом при x
= 0, в момент
прохождения положения равновесия и
равна
![]() .
.
Механическая энергия колебаний равна сумме кинетической и потенциальной энергий
![]() .
(14.4)
.
(14.4)
При прохождении маятником положения равновесия кинетическая энергия достигает максимального значения, а потенциальная энергия становится равной нулю. Через четверть периода в крайнем положении максимального значения достигает потенциальная энергия, а кинетическая энергия становится равной нулю. По закону сохранения механической энергии полная энергия свободных колебаний постоянна
![]() . (14.5)
. (14.5)
