8. Соударение тел

1. Явление удара

Удар – это процесс кратковременного взаимодействия тел, при котором происходит значительное изменение скоростей тел, их импульсов. Силы удара могут быть сравнительно большими, так как, согласно второму закону Ньютона, изменение импульса тела равно импульсу силы: , и при малом времени удара Dt сила удара F может быть большой. В этом случае действием внешних сил на время удара можно пренебречь и считать систему тел замкнутой. Поэтому для удара выполняется закон сохранения импульса: в замкнутой системе тел сумма импульсов постоянна, или сумма импульсов тел до взаимодействия равна сумме импульсов после взаимодействия

или . (8.1)

Явление удара осложнено такими процессами как излучение звуковых волн, распространение волн деформации в телах. Длительность удара можно оценить по времени отражения волн деформации. Например, молоток железнодорожный, в отличие от кувалды той же массы, имеет удлиненную форму. Поэтому время удара о забиваемый в шпалу костыль сравнительно больше, сила удара поменьше, а передаваемый костылю импульс тот же самый.

Существует две предельных идеализации реального удара: идеально упругий удар и абсолютно неупругий удар. При идеально упругом ударе тела в фазе сближения деформируются упруго, и часть кинетической энергии превращается в потенциальную энергию упругой деформации. Затем во второй фазе под действием упругих сил тела отталкиваются, форма тел восстанавливается, и потенциальная энергия деформации вновь превращается в кинетическую энергию. В результате при упругом ударе выполняется закон сохранения механической энергии.

При абсолютно неупругом ударе тела деформируются пластически. Удар заканчивается на фазе сближения, и затем тела движутся совместно, как одно целое. Это является признаком неупругого удара. Так как часть кинетической энергии превращается в работу пластической деформации, во внутреннюю энергию, то механическая энергия не сохраняется.

2. Соударение тел

Неупругий удар

Рассмотрим удар двух тел массами m₁ и m₂, скорости которых до удара V₁ и V₂ (рис. 8.1). Для неупругого удара можно применить только закон сохранения импульса, так как механическая энергия не сохраняется

. (8.1)

О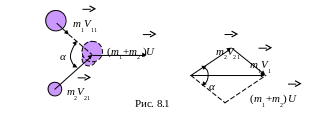 ткуда скорость совместного движения равна . Чтобы найти скорость шаров после удара, надо спроецировать уравнение (8.1) на выбранные оси координат и из уравнений определить проекции скорости U. Либо определить скорость U по векторной диаграмме, которая имеет вид треугольника, используя тригонометрические соотношения между сторонами треугольника.

Потери механической энергии при неупругом ударе превращаются во внутреннюю энергию тел, то есть в теплоту. Следовательно, теплоту можно определить как разность кинетических энергий до и после удара

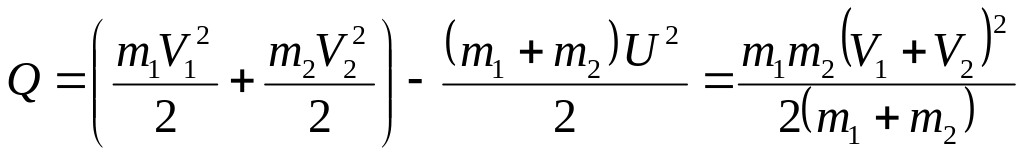. (8.2)

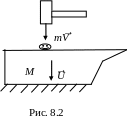
В технике явление неупругого удара применяют для двух целей. При ковке, штамповке деталей следует по возможности большую часть кинетической энергии молота массой m превратить в работу пластической деформации поковки. Для этого массу наковальни М делают как можно больше (рис. 8.2). Докажем это. По закону сохранения импульса для удара молота по наковальне определим скорость сотрясения наковальни U и затем энергию сотрясения . Тогда КПД тем больше, чем больше масса наковальни.

Наоборот, при забивании гвоздя молотком потери энергии на работу деформации должны меньше, а большая часть энергии молотка должна переходить в кинетическую энергию молотка с гвоздем после удара. Поэтому масса молотка должна быть больше массы гвоздя. Но так, чтобы гвоздь не согнулся.

Упругий удар

Для идеально упругого удара выполняются закон сохранения импульса и закон сохранения механической энергии. Рассмотрим идеально упругий центральный удар двух шаров, при котором скорости тел направлены по линии центров масс. Пусть начальные скорости направлены в одну сторону. Так как шары после удара отталкиваются друг от друга, то после удара они будут двигаться с неизвестными различными скоростями U₁ и U₂ по линии центров масс. Запишем закон сохранения импульса в проекции на направление движения первого шара и закон сохранения энергии

, (8.3)

. (8.4)

Имеем два уравнения с двумя неизвестными U₁ и U₂. Чтобы решение выполнить более просто, заменим уравнение с квадратами скоростей (8.4) третьим уравнением, которое получим, после преобразования уравнений (8.4) и (8.5).

, (8.5)

. (8.6)

После деления уравнений получим уравнение первой степени

. (8.7)

Решая совместно уравнения уже первого порядка (8.5) и (8.7), получим для скоростей тел после упругого удара формулы

, (8.8) . (8.9)

Рассмотрим частный случай, когда массы шаров равны: m₁ = m₂. Тогда скорости шаров после упругого удара будут равны . То есть, шары после удара обмениваются скоростями. А если второй шар до удара покоился, то после удара он будет двигаться со скоростью первого шара, а первый шар остановится.

При нецентральном ударе явление осложняется скольжением шаров в точке удара. Интересен случай упругого удара, при котором первый шар налетает на покоящийся второй шар равной массы, как в биллиарде. При ударе без трения энергия сохраняется. После сокращения на одинаковые массы уравнения законов сохранения импульса(8.3) и энергии (8.4) примут вид: и . Так как векторы первого уравнения образуют треугольник, то второе уравнение является теоремой Пифагора для этого треугольника. Следовательно, шары после удара разлетаются всегда под углом 90^о.