7. Линейные модели оптимизации в Excel.

32. При решении оптимизационных задач в Excel с помощью Поиск решений (Solver) необходимо различать линейные и нелинейные модели. Под линейными понимаются модели, в которых связь между ограничениями на неизвестные и целевой ячейкой описывается линейными функциями. Общий вид линейной функции: Y=AX1+BX2+…+CXn, где A, B, C – константы, X1, X2, X3 – переменные, Y – результирующие значение.

Линейное программирование – наиболее разветый раздел математического программирования, вычислительные средства которого позволяют находить глобальний оптимум линейной задачи оптимизации.

Линейные модели используют свойство линейных задач оптимизации, как линейные уровнения или неравенство на неизвестные и целевую функцию. Это означает, что область допустимых решений - выпуклой многоугольник, одна из вершин которого и есть оптимальное решение

Построение линейной модели оптимизации в программе Excel с помощью функции «Поиска решения».

1.  Создать таблицу с формулами, которые устанавливают связи между ячейками.

2. Выделить целевую ячейку, которая должна принять необходимое значение, и выбрать команду: Поиск решения.

3. Установить переключатели, задающие значение целевой ячейки на максимальное, минимальное или другое значение. В последнем случае введите значение в поле справа.

4. Указать в поле «Изменяя ячейки», в каких ячейках программа должна изменять значения в поисках оптимального результата.

5. С 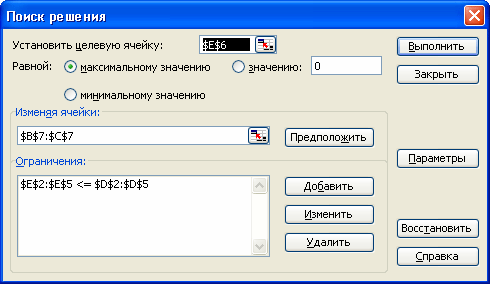оздать ограничения в списке «Ограничения». Для этого щелкните на кнопке «Добавить» и в диалоговом окне «Добавление ограничения» определите ограничение.

6. Щелкнеть на кнопке Параметры, и в появившемся окне установите переключатель Неотрицательные значения (если переменные должны быть позитивными числами), Линейная модель (если задача, которую вы решаете, относится к линейным моделям).

7. Щелкнув на кнопке «Выполнить», запустить процесс поиска решения.

8 . Когда появится диалоговое окно «Результаты поиска решения», выбрать переключатель «Сохранить найденное решение» или «Восстановить исходные значения». 9. Щелкните на кнопке ОК.

 

33. Задача распределения ресурсов.

Пусть бригада имеет: 300 кг металла, 100 м² стекла, 160 чел. — час. рабочего времени. Надо изготовить: изделия А и В. Прибыль от реализации изделий: А — 10 у.е., В — 12 у.е. Для изготовления изделия А расходуется: 4 кг металла, 2 м² стекла и 2 чел.—час. рабочего времени. Для изготовления изделия В расходуется: 5 кг металла, 1 м² стекла и 3 чел.­ — час. рабочего времени. Требуется спланировать выпуск продукции так, чтобы прибыль была максимальной.

Математическая постановка задачи.

Пусть и — количество изделий А и В, тогда ресурсы сырья и рабочего времени запишем в виде ограничений—неравенств:

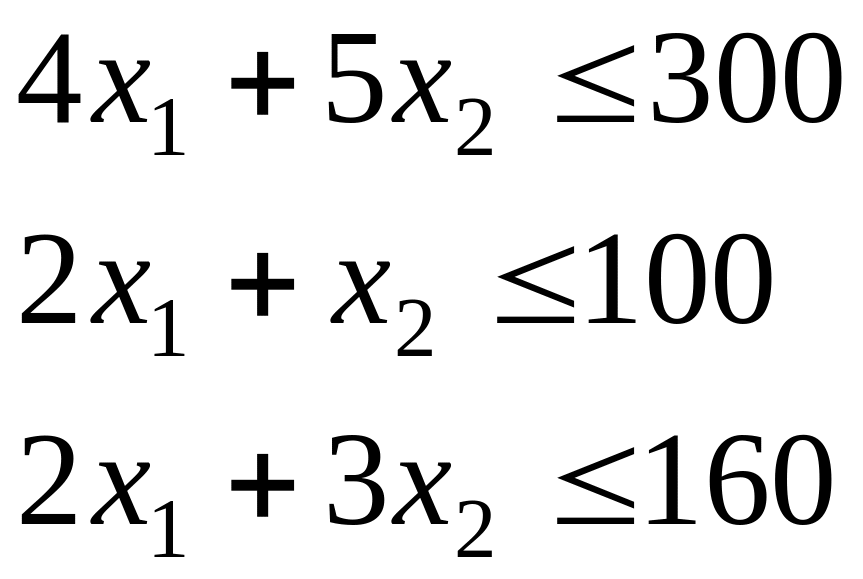
Прибыль от реализации всей продукции составит

Это типичная задача линейного программирования ( ). Вид данной задачи не канонический, поскольку условия имеют вид неравенств, а не уравнений. Сведем ее к каноническому виду, добавив дополнительные переменные по числу ограничений—неравенств:

При этом .

Выделение новых переменных не влияет на вид целевой функции. Они будут указывать на остатки ресурсов, не использованные в производстве.

Чтобы свести данную задачу к задаче минимизации целевой функции, функцию нужно взять со знаком минус:

Запишем условие задачи в виде таблицы

Примем в качестве базисных переменные и перейдем к этому новому базису. В результате получим следующую таблицу:

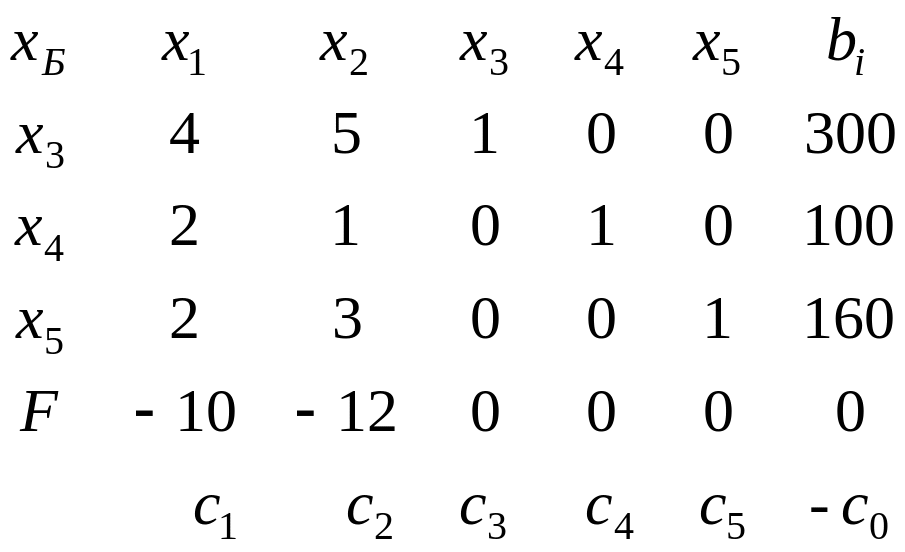
Так как все , то в качестве начального опорного решения можно взять следующее решение:

Этому решению соответствует значение целевой функции

Оно не оптимально, так как эта величина может быть уменьшена за счет свободных параметров (коэффициенты и при неизвестных и в целевой функции отрицательны). Наибольшим среди всех отрицательных является коэффициент , которому соответствует переменная . Определим базисную переменную, которая первой станет равной 0 при увеличении значения . Для этого вычислим следующие величины:

Наименьшей является величина 53,3, которая соответствует переменной . Определим новое опорное решение:

Значение целевой функции

Это решение уже лучше.

Следующий шаг начнем с выбора нового базиса. Примем переменные в качестве базисных и перейдем к этому базису. Результаты представлены в следующей таблице:

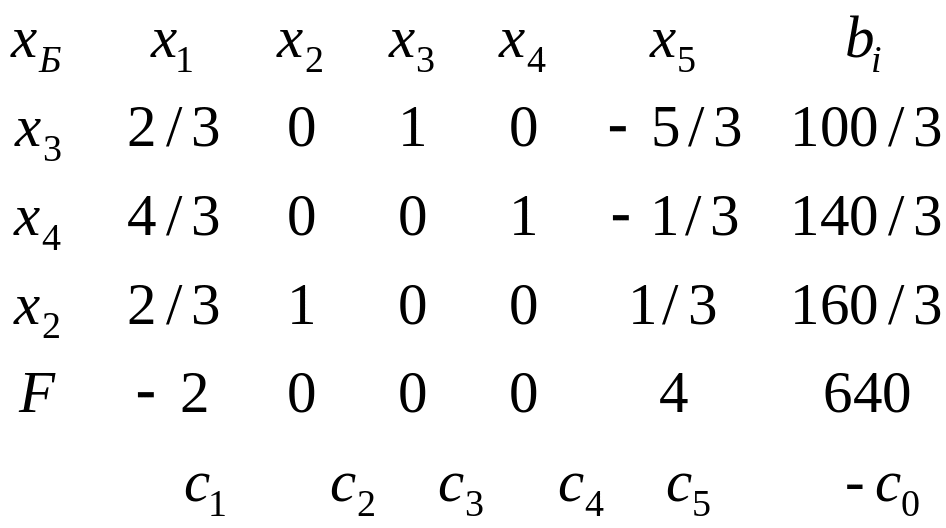
Этому решению соответствует значение целевой функции

Оно не оптимально, так как эта величина может быть уменьшена за счет свободного параметра (коэффициент при неизвестном в целевой функции отрицателен). Определим базисную переменную, которая первой станет равной 0 при увеличении значения . Для этого вычислим следующие величины:

Наименьшей является величина 35, которая соответствует переменной . Определим новое опорное решение:

Значение целевой функции

Это решение еще лучше предыдущего.

Следующий шаг начнем с выбора нового базиса. Примем переменные в качестве базисных и перейдем к этому базису. Результаты представлены в следующей таблице:

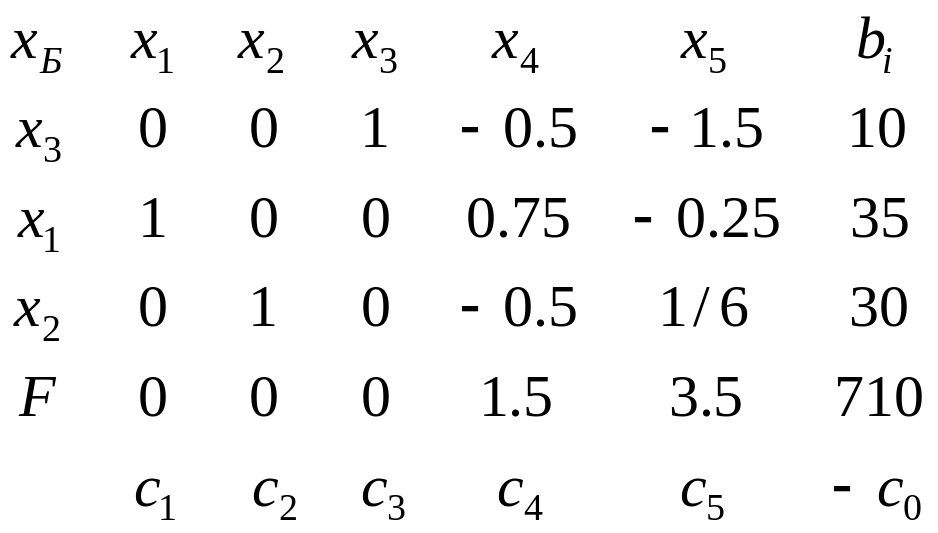
Коэффициенты при свободных неизвестных в целевой функции положительны, поэтому, при их увеличении целевая функция может лишь увеличиваться. Следовательно, решение, полученное на предыдущем шаге, является оптимальным, а значение целевой функции равно

Ответ: Для получение максимума прибыли в 710 у.е. необходимо изготовить 35 изделий А и 30 изделий В. При этом все ресурсы стекла и рабочего времени будут использованы полностью, а металла останется 10 кг.

34. Транспортная задача — математическая задача линейного программирования специального вида о поиске оптимального распределения однородных объектов из аккумулятора к приемникам с минимизацией затрат на перемещение. Для простоты понимания рассматривается как задача об оптимальном плане перевозок грузов из пунктов отправления в пункты потребления, с минимальными затратами на перевозки.