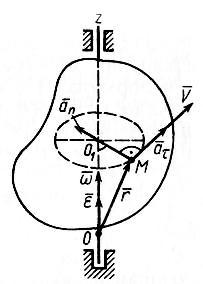
В екторные формулы для скоростей и ускорений точек тела

Выразим скорость, касательное, нормальное и полное ускорения точки тела в векторной форме (рис. 19).

,

Это выражение называется векторной формулой Эйлера.

,

так как .

В частности, в качестве радиуса-вектора можно использовать вектор , направив его из точки О₁ в точку М.

И

Рис. 19

з определения ускорения и векторной формулы Эйлера имеем

.

Учитывая, что

; ,

получаем

.

Первое слагаемое является касательным ускорением, а второе – нормальным, т. е.

; .

В справедливости этой формулы убеждаемся вычислением их правых частей. Имеем (рис. 20)

Рис. 20

,

4. Сложное движение точки

В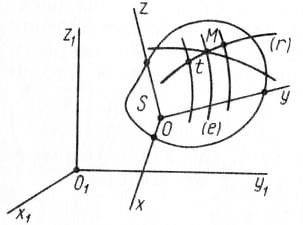 простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения. Пусть имеем две системы отсчета, движущиеся друг относительно друга. Если одну из этих систем O₁x₁y₁z₁ (рис. 21) принять за основную или неподвижную (ее движение относительно других систем отсчета не рассматривается), то вторая система отсчета Oxyz будет двигаться относительно первой. Движение точки относительно подвижной системы отсчета Oxyz называется относительным.

Д

Рис. 21

вижение точки относительно основной, или неподвижной, системы отсчета O₁x₁y₁z₁ называется абсолютным (или сложным). Его также иногда называют составным движением. Траектория, скорость и ускорение этого движения называются абсолютными. Переносным движением точки называют движение, которое она совершает вместе с подвижной системой отсчета, как точка, жестко скрепленная с этой системой в рассматриваемый момент времени. Переносной скоростью и переносным ускорением являются скорость и ускорение той точки тела S, с которой в данный момент совпадает движущаяся точка. Переносные скорость и ускорение обозначают , .

С ложение скоростей

О

Рис. 22

пределим скорость абсолютного известны скорости относительного и этой точки. Пусть точка совершает только одно относительное движение по отношению к подвижной системе отсчета Oxyz и в момент времени t занимает на траектории относительного движения положение М (рис. 22). В момент времени вследствие относительного движения точка окажется в положении М₁ совершив перемещение ММ₁ по траектории относительного движения. Предположим, что точка участвует только в одном переносном движении. Тогда за время вследствие этого движения вместе с системой координат Oxyz и относительной траекторией она переместится по некоторой кривой на ММ₂ Если точка участвует одновременно и в относительном и в переносном движениях, то за время она переместится на ММ' по траектории абсолютного движения и в момент времени займет положение М'. Если время мало и в дальнейшем переходят к пределу при , стремящемся к нулю, то малые перемещения по кривым можно заменить отрезками хорд и принять их за векторы перемещений. Складывая векторные перемещения, получаем

; .

Переходя к пределу, имеем

.

; ; .

Следовательно,

.

Получена так называемая теорема сложения скоростей: скорость абсолютного движения точки равна векторной сумме скоростей переносного и относительного движений этой точки.