7. Скорость и ускорение точки в цилиндрических координатах.

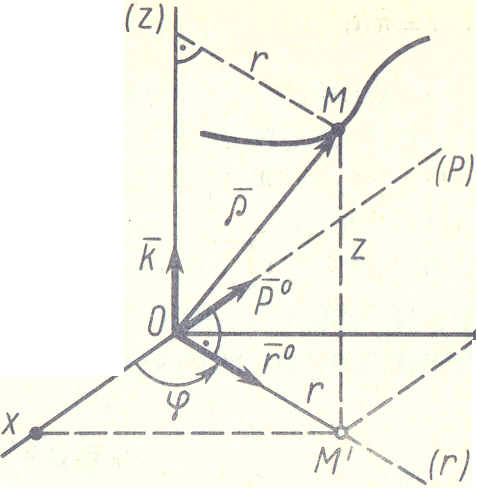
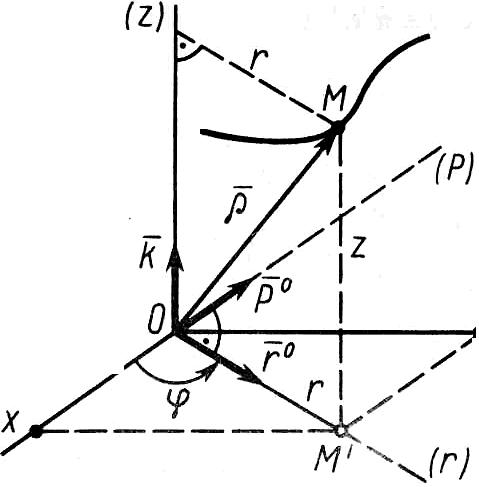
При движении точки в пространстве иногда используются цилиндрические оси координат. Они получаются добавлением к полярным координатам на плоскости координаты z, отчисляемой вдоль неподвижной оси Oz (рис. 11). Положение точки М определяют заданием трёх её цилиндрических координат как функций времени:

где , , - единичные векторы, направленные по осям цилиндрической системы координат. Оси Or и Op расположены в одной плоскости с осями Ox и Oy.

Представим радиус – вектор точки М как сумму двух векторов, т.е.

Рис. 11

Скорость точки получим дифференцированием радиуса – вектора по времени:

Первое слагаемое в этом выражении вычислялось при выводе формулы для скорости точки в полярных координатах. Было получено

Во втором слагаемом постоянным по модулю и направлению единичный вектор можно вынести за знак производной. Для скорости получается следующее разложение на составляющие, параллельные осям цилиндрической системы координат:

Отсюда получаем формулы для проекций скорости на цилиндрические оси координат:

Так как составляющие скорости , и , параллельные осям цилиндрической системы координат, взаимно перпендикулярны, то для модуля скорости имеем

Ускорение точки получим дифференцированием по времени вектора скорости:

Первое слагаемое в этом выражении вычислялось при выводе ускорения в полярных координатах:

Во втором слагаемом при дифференцировании выносим вектор за знак производной. Объединяя результаты дифференцирования, получим следующее разложение ускорения на составляющие, параллельные осям цилиндрической системы координат:

Отсюда получаем формулы для проекций ускорения на цилиндрические оси координат

.

Составляющие ускорения , и , взаимно перпендикулярны, поэтому для модуля ускорения имеем:

8. Скорость и ускорение точки в криволинейных координатах

Положение точки в пространстве в декартовой системе координат определяется тремя координатами: x, y, z. Можно выбрать другие три параметра и назвать их криволинейными или обобщёнными координатами точки. Декартовы координаты будут зависеть от криволинейных:

Движение точки в криволинейных координатах задаётся уравнениями

Радиус – вектор движущейся точки, начало которого находится в неподвижной точке выбранной системы отсчёта для рассматриваемого движения, является функцией как декартовых, так и криволинейных координат, т.е.

Выберем точку О, в которой криволинейные координаты равны нулю, и рассмотрим зависимость Получим уравнение в векторной форме координатной линии для , проходящей через точку О. Аналогично получаются уравнения координатных линий и ,проходящих через точку О для координат и .

Через каждую точку пространства можно провести три координатных линии, пересекающиеся в этой точке. Вдоль каждой из координатных линий изменяется только одна криволинейная координата, а две другие сохраняют постоянные значения, соответствующие рассматриваемой точке.

Рассмотрим частные производные . Они как производные от вектора по скалярному аргументу направлены по касательным к координатным линиям, являющиеся годографами радиуса – вектора. Введём единичные векторы, направленные по векторам . Эти три единичных вектора называются базисными векторами. Базисные векторы, как , направлены в каждой точке по касательным к координатным линиям в сторону возрастания криволинейных координат. Направления возрастания и начало отсчёта криволинейных координат выбираются при задании движения.

В общем случае базисные векторы могут быть неортогональными. Используя базисные векторы, получаем

или

(i=1, 2, 3).

Скалярные величины = называются коэффициентами Ламэ.

Для вычисления учтём, что радиус – вектор через декартовы координаты можно выразить в форме

где , , - единичные векторы, направленные по осям декартовой системы координат. Отсюда получаем

и, следовательно,

Скорость точки в криволинейных координатах. При движении точки её радиус – вектор через обобщённые координаты зависит от времени, т.е.

По определению скорости и правила дифференцирования сложных функций имеем

где называется обобщённой скоростью точки.

Используя ранее полученные формулы, получаем

.

Получено разложение скорости по осям, направление которых совпадает с направлением базисных векторов. Для величин составляющих скорости по базисным векторам имеем

( i=1,2,3 ).

В случае ортогональности базисных векторов вычисляются проекции вектора скорости на оси, направленные по базисным векторам. В этом случае для квадрата скорости получаем

.

Ускорение в ортогональных криволинейных координатах. Криволинейные координаты считаются ортогональными, если ортогональны их базисные векторы. В приложениях обычно встречается этот случай. Для ортогональных базисных векторов проекции ускорения точки на их направления вычисляем по формулам

( i=1,2,3 ).

Выражая базисные векторы, получим

. (1)

Для дальнейшего преобразования следует воспользоваться тождествами

(2)

или (3)

или . (4)

Тождество (2) представляют собой известное правило дифференцирования скалярного произведения двух векторов. Докажем справедливость тождеств Лагранжа (3) и (4).

Тождество (3) получим дифференцированием , например, по . Учитывая, что производные не могут зависеть от , имеем

.

Аналогично,

т.е. ( i=1,2,3 ).

Справедливость тождества (3) установлена.

Для доказательства тождества (4) продифференцируем по . Получим

(5)

Учитывая, что не может зависеть от обобщённых скоростей, и дифференцируя её по времени как сложную функцию времени, имеем

(6)

Правые части (5) и (6) совпадают, так как они отличаются только порядком частного дифференцирования, от которого частные производные не зависят. Следовательно, тождество (4) доказано. Используя тождества, преобразуем выражение в скобках из (1). Получим

(7)

Учитывая, что , и вводя функцию , из (1) с учётом (7) имеем

( i=1,2,3 ). (8)

По формулам (8) можно вычислить проекции ускорения точки на оси, направленные по базисным ортогональным векторам.