2. Погашення кредиту частками

2.1) Погашення основної суми кредиту рівними частками.

При погашенні кредиту частками поточне значення суми боргу після чергової виплати буде зменшуватися і, відповідно буде зменшуватися сума процентів, нарахованих на наступному інтервалі. Якщо сума кредиту дорівнює D, термін кредиту дорівнює n і він погашається рівними частками, в кінці кожного року, то розмір суми виплачених процентів в кінці кожного року буде дорівнювати:

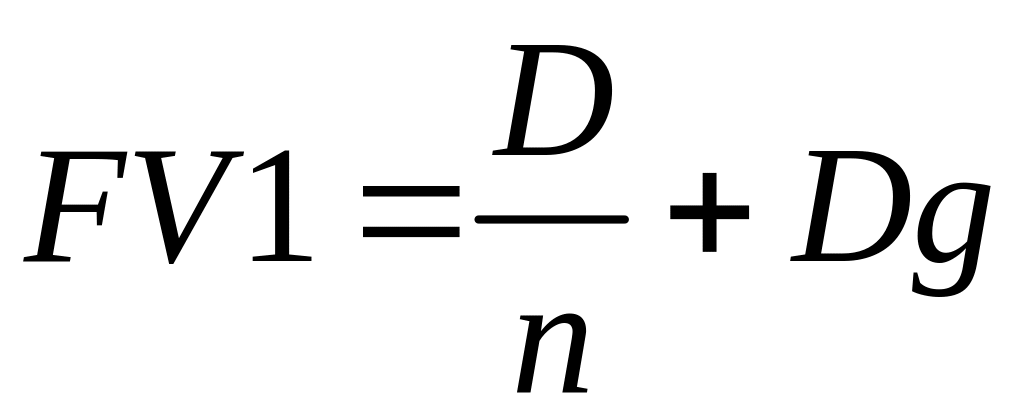. (3)

де, g – річна процентна ставка за кредитом.

Залишок боргу на початок 2-го року дорівнює:

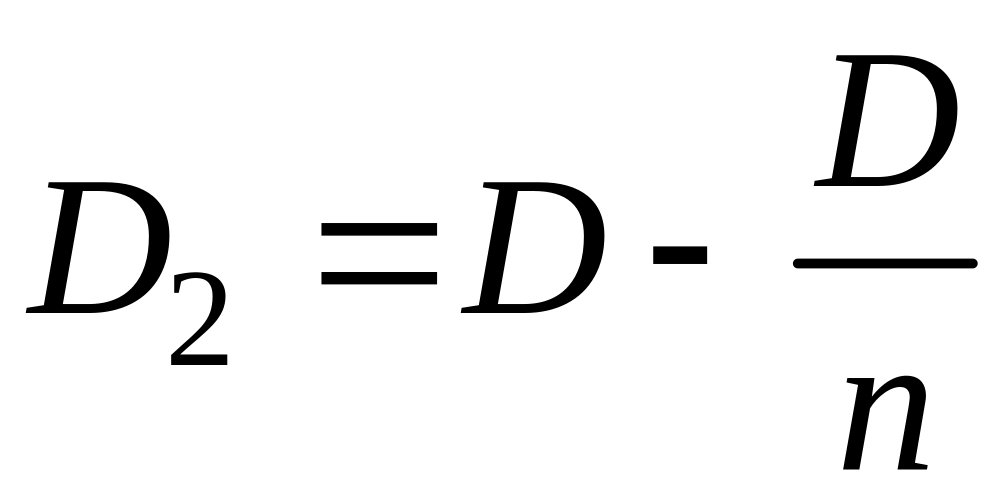. (4)

Розмір суми виплачених процентів в кінці терміну кредиту буде дорівнювати:

. (5)

Загальна сума погашення кредиту, тоді буде дорівнювати:

. (6)

Якщо внески в погашення кредиту будуть здійснюватися р разів на рік, сума сплачених процентів буде визначатися за формулою:

. (7)

Приклад 4. Кредит в розмірі 5 000 000 грн., виданий за ставкою 80% річних повинен погашатися рівними сумами протягом 5 років. Визначити розміри щорічних виплат (план погашення) і суму сплачених процентів, якщо погашення відбувається по півріччях.

1-метод

За формулою (3) визначимо суму виплат в кінці першого року

грн..

Заборгованість по кредиту на другий рік за формулою (4)

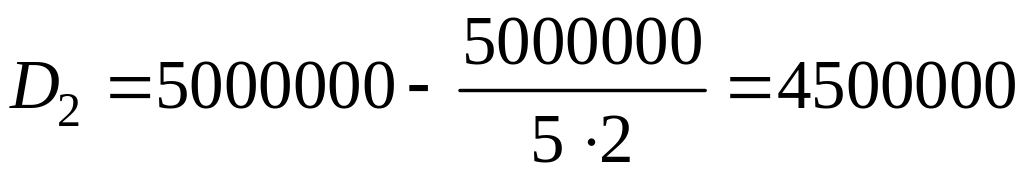грн.

FV2 = 2.3; D3 = 4.0; FV3 = 2.1; D4 =3.5; FV4 = 3.5; D5 = 3.0; FV5 = 1.7; D6 =2.5;

FV6 = 1.5; D7 = 2.0; FV7 = 1.3; D8 =1.5; FV8 = 1.1; D9 = 1.0; FV9 = 0.9; D10 =0.5;

FV10 = 0.7; D11 =0.

Загальні витрати по погашенню кредиту

FV = 2.5+2.3+2.1+1.9+1.7+1.5+1.3+1.1+0.9+0.7=16 млн. грн.

Сума виплачених процентів

І = 16 млн. – 5 млн. = 11 млн. грн.

2-метод

За формулою (7)

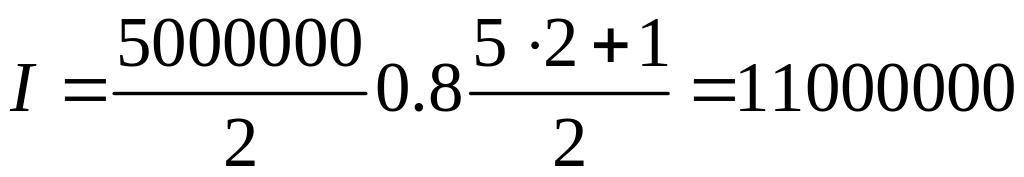грн.

2.2) Погашення кредиту рівними терміновими частками.

2.2.1) Прості проценти

Розмір однакових термінових виплат R по кредиту з нарахуванням простих процентів буде розраховуватися за формулою:

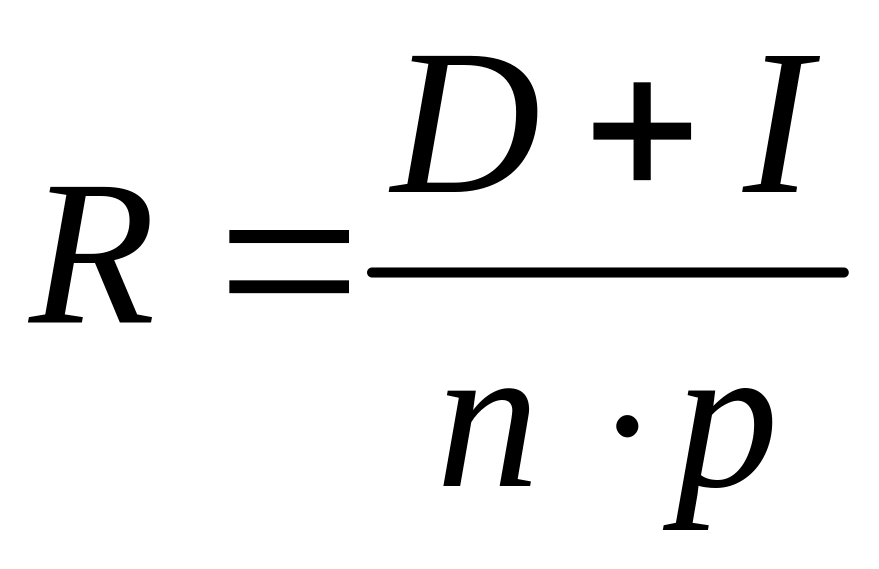. (8)

де, n – термін кредиту в роках

p – кількість виплат за кредит на рік

I – сума нарахованих процентів.

Приклад 5. Споживчій кредит на суму 600 000 грн. відкритий на 2 роки за ставкою 40% річних. Погашення кредиту повинно здійснюватися рівними внесками. Визначити суму процентів по кредиту, суму погашення і розмір внесків, якщо погашення кредиту буде відбуватися щомісячно.

За формулою (7) визначаємо суму процентів за кредит

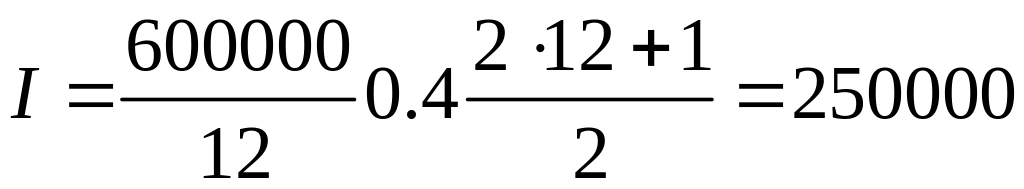грн..

Сума погашення = розмір кредиту + сума процентів = 600 000 + 250 000 = 850 000 грн.

Розмір щомісячних внесків за формулою (8)

грн.

2.2.2) Складні проценти

Розмір однакових термінових виплат R по кредиту D в кінці кожного року з нарахуванням складних процентів i буде розраховуватися за формулою:

. (9)

Загальна сума погашення кредиту складе:

. (10)

Сума процентів

. (11)

Якщо рівні виплати по кредиту в розмірі R будуть вноситися р разів на рік, їх розмір буде розраховуватися:

. (11)

Приклад 6. Кредит в розмірі 10 млн. грн. з щорічним нарахуванням складних процентів за ставкою 20% річних повинен погашатися протягом 5 років рівними терміновими виплатами. Визначити розмір термінових виплат, суму погашення кредиту і суму сплачених процентів, якщо виплати по кредиту будуть здійснюватися в кінці кожного півріччя.

Розмір виплат за формулою (11)

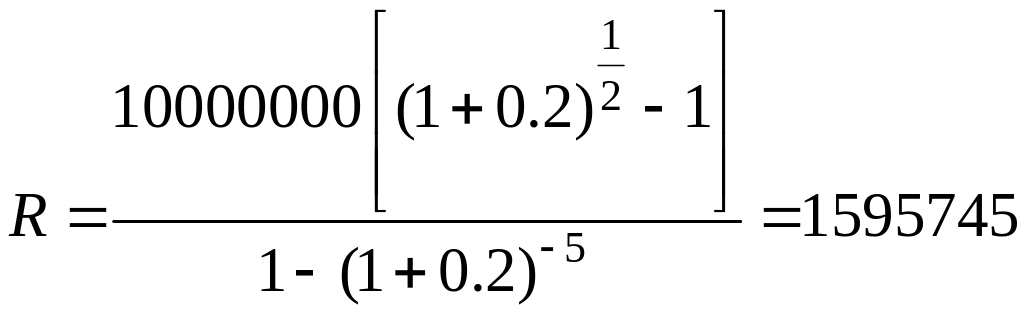грн.

Сума погашення за формулою (10)

FV = 10 * 1595745 = 15957450 грн.

Сума виплачених процентів за формулою (11)

І = 15957450 – 10000000 = 5957450 грн.